2019学年高二数学10月月考试题 文 人教版

2019学年高二数学10月月考试题 文 人教版

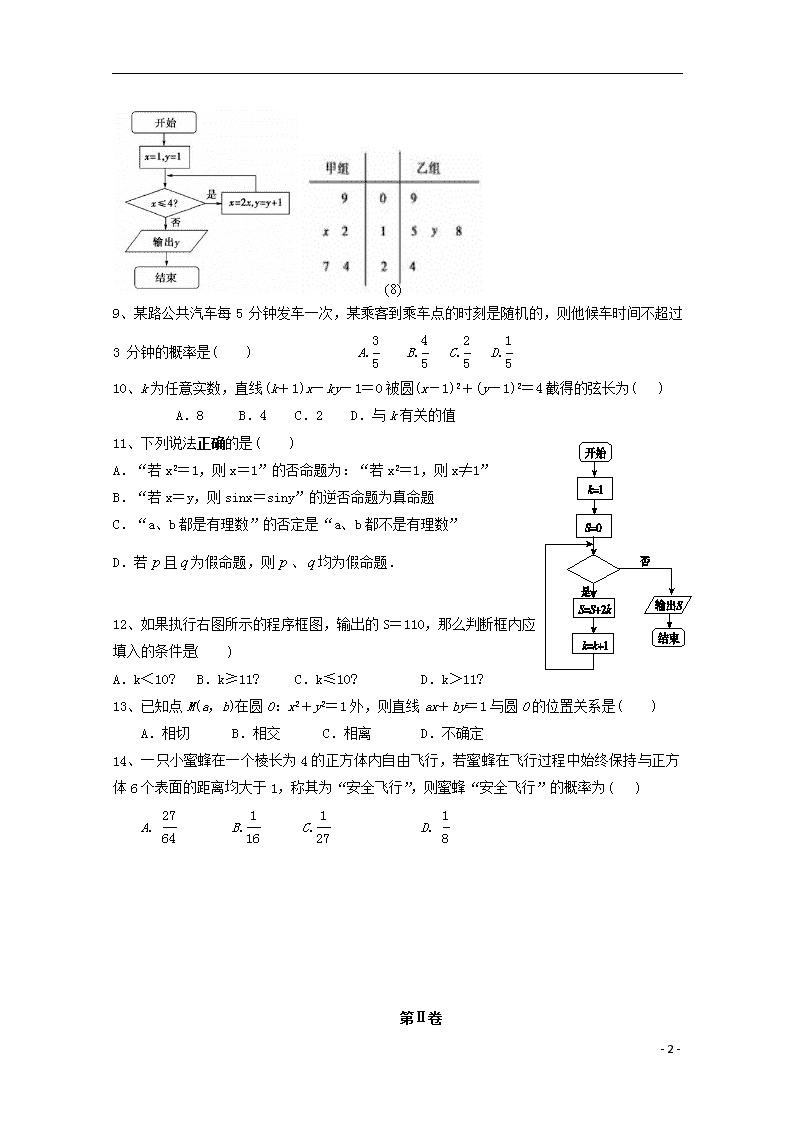
‎2019学年度第一学期10月月考试卷 高二文科数学 ‎ ‎ 第I卷 一、选择题：(本大题共14小题，每小题5分，共70分.)‎ ‎1、老师在班级50名学生中，依次抽取学号为5,10,15,20,25,30,35,40,45,50的学生进行作业检查，这种抽样方法是(　　) A． 简单随机抽样　B．分层抽样 C．系统抽样 D．以上都不是 ‎2、从装有2个红球和2个白球的口袋中任取两球，那么事件“至少有一个白球”的互斥事件为（ ）‎ A至多一个白球 B至少有一个红球 C恰有2个白球 D都是红球 ‎3、已知集合A＝{1，a}，B＝{1,2,3}，则“a＝3”是“A⊆B”的(　)‎ A．充分不必要条件B．必要不充分条件C．充要条件 D．既不充分也不必要条件 ‎4、用秦九韶算法求n次多项式f(x)＝ax＋a x＋…＋ax＋a的值，当x＝x时，求f(x)需要算乘法、加法的次数分别为(　　)‎ A. n-1，n        B．2n，n C．2n，n        D．n，n ‎ ‎5、下列对一组数据的分析，不正确的说法是( )‎ A、数据极差越小，样本数据分布越集中、稳定 B、数据标准差越小，样本数据分布越集中、稳定 C、数据平均数越小，样本数据分布越集中、稳定 D、数据方差越小，样本数据分布越集中、稳定 ‎6、已知命题p：∀x＞0，总有(x＋1)ex＞1，则p为(　　)‎ A．∃x0≤0，使得(x0＋1)ex0≤1 B．∃x0＞0，使得(x0＋1)ex0≤1‎ C．∀x＞0，总有(x＋1)ex≤1 D．∀x≤0，总有(x＋1)ex≤1‎ ‎7、如图所示，程序框图(算法流程图)的输出结果是(　　)‎ ‎ A． 4　　 B． 3　　C． 5　   D． 8‎ ‎8、如图所示的茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位：分)。已知甲组数据的中位数为15，乙组数据的平均数为16.8，则x，y的值分别为(　　)‎ A．2, 5        B．5, 5 C．8, 8      D．5, 8‎ - 6 -‎ ‎(8)‎ ‎9、某路公共汽车每5 分钟发车一次，某乘客到乘车点的时刻是随机的，则他候车时间不超过3 分钟的概率是( 　) A. B. C. D. ‎10、k为任意实数，直线(k＋1)x－ky－1＝0被圆(x－1)2＋(y－1)2＝4截得的弦长为(　 )‎ A．8 B．4 C．2 D．与k有关的值 ‎11、下列说法正确的是( 　)‎ A．“若x2＝1，则x＝1”的否命题为：“若x2＝1，则x≠1”‎ B．“若x＝y，则sinx＝siny”的逆否命题为真命题 C．“a、b都是有理数”的否定是“a、b都不是有理数”‎ D．若且为假命题，则、均为假命题．‎ ‎12、如果执行右图所示的程序框图，输出的S＝110，那么判断框内应填入的条件是(　　)‎ A．k＜10? B．k≥11? C．k≤10? D．k＞11?‎ ‎13、已知点M(a，b)在圆O：x2＋y2＝1外，则直线ax＋by＝1与圆O的位置关系是(　　)‎ A．相切　　 B．相交 C．相离 D．不确定 ‎14、一只小蜜蜂在一个棱长为4的正方体内自由飞行，若蜜蜂在飞行过程中始终保持与正方体6个表面的距离均大于1，称其为“安全飞行”，则蜜蜂“安全飞行”的概率为( )‎ A. B. C. D. ‎  第Ⅱ卷 - 6 -‎ 二. 填空题：（本大题共4小题，每小题5分，共20分。）‎ ‎15、一支游泳队有男运动员32人，女运动员24人，若用分层抽样的方法从该队的全体运动员中抽取一个容量为14的样本，则抽取男运动员的人数为______． ‎ ‎16、为了均衡教育资源，加大对偏远地区的教育投入，调查了某地若干户家庭的年收入x(单位：万元)和年教育支出y(单位：万元)，调查显示年收入x与年教育支出y具有线性相关关系，并由调查数据得到y对x的回归直线方程：=0.15x＋0.2.由回归直线方程可知，家庭年收入每增加1万元，年教育支出平均增加__________万元．‎ ‎17、若命题“∃x∈R，有x2－mx－m＜0”是假命题，则实数m的取值范围用区间表示为__________．‎ ‎18、天气预报说，在今后的三天中，每一天下雨的概率均为40%．现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率：先利用计算器产生0到9之间取整数值的随机数，用1，2，3，4表示下雨，用5，6，7，8，9，0表示不下雨；再以每三个随机数作为一组，代表这三天的下雨情况．经随机模拟试验产生了如下20组随机数： ‎ ‎907 966 191 925 271 932 812 458 569 683‎ ‎431 257 393 027 556 488 730 113 537 989‎ 据此估计，这三天中恰有两天下雨的概率近似为_________．‎ 三、解答题：（本大题共5小题，每小题12分，共60分。）‎ ‎19、现有5道题，其中3道甲类题，2道乙类题，张同学从中任取2道题解答．试求：‎ ‎(1)所取的2道题都是甲类题的概率；‎ ‎(2)所取的2道题不是同一类题的概率．‎ ‎20、给定两个命题，P：对任意的实数x都有恒成立；Q：关于x的方程有实数根；如果为真，为假，求实数a的取值范围。‎ ‎21、某校100名学生期中考试语文成绩的频率分布直方图如图4所示，其中成绩分组区间是：‎ ‎[50,60][60,70][70,80][80,90][90,100]。‎ ‎(1)求图中的值；‎ ‎(2)根据频率分布直方图，估计这100名学生语文成绩的平均分；‎ ‎(3)若这100名学生语文成绩某些分数段的人数()与数学成绩相应分数段的人数()之比如下表所示，求数学成绩在[50，90)之外的人数。‎ - 6 -‎ ‎22．某农科所对冬季昼夜温差大小与某反季大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了2015年12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数，得到如下表：‎ 日期 ‎12月1日 ‎12月2日 ‎12月3日 ‎12月4日 ‎12月5日 温差x(℃)‎ ‎10‎ ‎11‎ ‎13‎ ‎12‎ ‎8‎ 发芽数y(颗)‎ ‎23‎ ‎25‎ ‎30‎ ‎26‎ ‎16‎ 该农科所确定的研究方案是：先从这五组数据中选取2组，用剩下的3组数据求线性回归方程，再对被选取的2组数据进行检验．‎ ‎(1)若选取的是12月1日与12月5日的两组数据，请根据12月2日至12月4日的数据，求出y关于x的线性回归方程＝bx＋a；‎ ‎(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问(2)中所得到的线性回归方程是否可靠？‎ ‎23．投掷一个质地均匀的、每个面上标有一个数字的正方体玩具，它的六个面中，有两个面标的数字是0，两个面标的数字是2，两个面标的数字是4，将此玩具连续抛掷两次，以两次朝上一面的数字分别作为点P的横坐标和纵坐标．‎ ‎(1)求点P落在区域C：x2＋y2≤10内的概率；‎ ‎(2)若以落在区域C上的所有点为顶点作面积最大的多边形区域M，在区域C上随机撒一粒豆子，求豆子落在区域M上的概率．‎ - 6 -‎ 鹿泉一中2016—2017学年度第一学期10月月考 高二文科数学答案 一、 选择题：CDADC BADAB BCBD ‎ 二、 填空题： 15、8 16、0.15 17、[－4,0] 18、 0.25 ‎ 三、解答题 ‎19、(1)将3道甲类题依次编号为1,2,3,；2道乙类题依次编号为4,5，任取2道题，基本事件为：{1,2}，{1,3}，{1,4}，{1,5}，{2,3}，{2,4}，{2,5}，{3,4}，{3,5}，{4,5}共10个，而且这些基本事件的出现是等可能的．用A表示“都是甲类题”这一事件，则A包含的基本事件有{1, 2}，{1,3}，{2,3}共3个，所以P(A)＝ ‎(2)基本事件同(1)，用B表示“不是同一类题”这一事件，则B包含的基本事件有{1,4}，{1,5}，{2,4}，{2,5}，{3,4}，{3,5}共6个，所以P(B)＝ ‎20、解：设P为真时，a的取值集合为A，Q为真是a的取值集合为B。‎ 据题意得:， ——3分 ‎ ——6分 为真，为假，即p和q有且仅有一个为真，a的取值范围即为： ——12分 ‎21、(1)。‎ ‎(2)平均分为。‎ ‎(3)数学成绩在内的人数为人，数学成绩在外的人数为人。‎ ‎22、(1)由数据，求得＝12，＝27.‎ - 6 -‎ 由公式，求得b＝，a＝－b ＝－3.‎ 所以y关于x的线性回归方程为＝x－3.‎ ‎(2)当x＝10，＝×10－3＝22，|22－23|＜2；‎ 同样，当x＝8时，＝×8－3＝17，|17－16|＜2；‎ 所以，该研究所得到的回归方程是可靠的．‎ ‎23、(1)以0、2、4为横、纵坐标的点P共有(0,0)、(0,2)、(0,4)、(2,0)、(2,2)、(2,4)、(4,0)、(4,2)、(4,4)共9个，而这些点中，落在区域C内的点有：(0,0)、(0,2)、(2,0)、(2,2)共4个，故所求概率为P＝.‎ ‎(2)∵区域M的面积为4，而区域C的面积为10π，‎ ‎∴所求概率为P＝＝.‎ ‎ ‎ - 6 -‎