2020届二轮复习算法学案(全国通用)
算法
算法(algorithm)是指按照一定规则解决某一类问题的明确和有限的步骤.
可以理解为由基本运算及规定的运算顺序所构成的完整的解题步骤,或者看成按照要求设计好的有限的确切的计算序列,并且这样的步骤或序列能够解决一类问题.
描述算法可以有不同的方式.例如,可以用自然语言和数学语言加以描述,也可以借助形式语言(算法语言)给出精确的说明,也可以用框图直观地显示算法的全貌.
算法的要求:
(1)写出的算法,必须能解决一类问题,并且能重复使用;
(2)算法过程要能一步一步执行,每一步执行的操作必须确切,不能含混不清,而且经过有限步后能得到结果.
程序框图
· 程序框图
程序框图简称框图,是一种用程序框、流程线及文字说明来表示算法的图形.
其中,起、止框是任何流程不可少的,表明程序的开始和结束.输入和输出框可用在算法中任何需要输入、输出的位置.算法中间要处理数据或计算,可分别写在不同的处理框内.一个算
法步骤到另一个算法步骤用流程线连接.如果一个框图需要分开来画,要在断开处画上连接点,并标出连接的号码.
· 画程序框图的规则
(1)使用标准的图形符号.
(2)框图一般按从上到下、从左到右的方向画.
(3)除判断框外,大多数流程图符号只有一个进入点和一个退出点.判断框是具有超过一个退出点的惟一符号.
(4)判断框分两大类,一类判断框是“是”与“否”两分支的判断,而且有且仅有两个结果;另一类是多分支判断,有几种不同的结果.
(5)在图形符号内描述的语言要非常简练清楚.
· 算法的三种基本逻辑结构
顺序结构:语句与语句之间,框与框之间按从上到下的顺序进行.
条件分支结构:在一个算法中,经常会遇到一些条件的判断,算法的流程条件是否成立有不同的流向,条件结构就是处理这种过程的结构.
循环结构:在一些算法中,经常会出现从某处开始,按照一定的条件反复执行某些步骤的情况,这就是循环结构.
程序语句
程序设计语言有很多种,以类BASIC语句为例说明常用的语句:
输入语句
输出语句
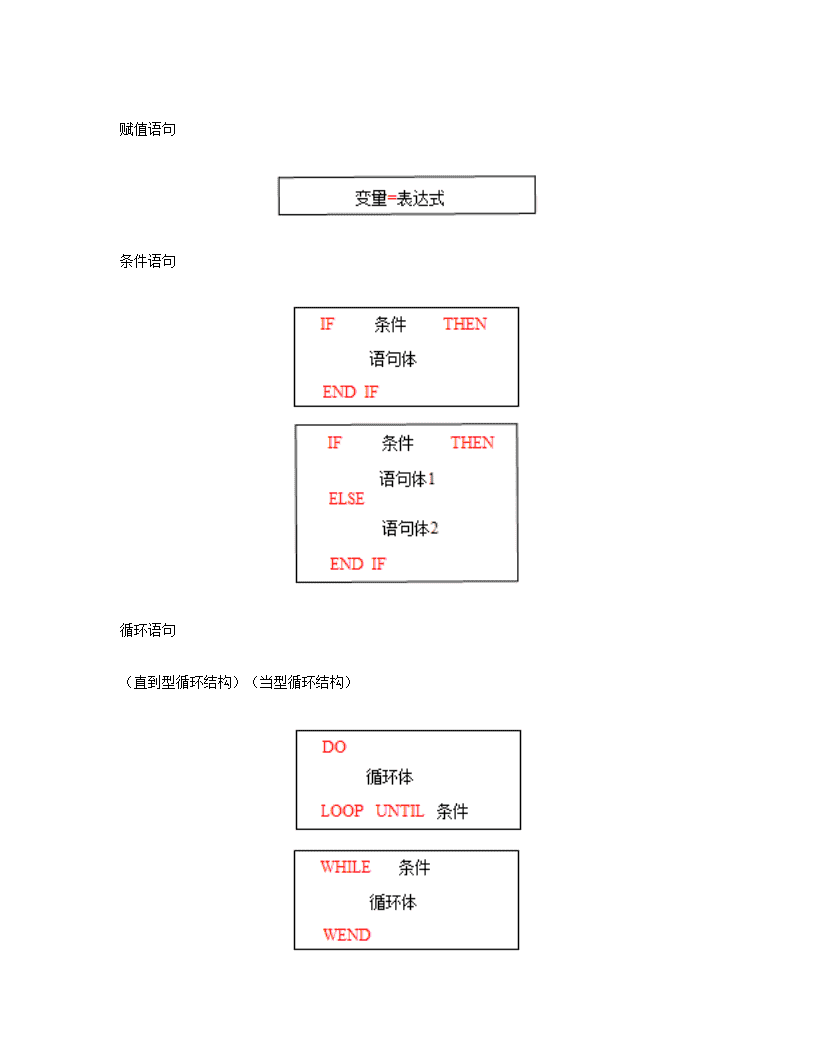
赋值语句
条件语句
循环语句
(直到型循环结构)(当型循环结构)
高中数学常用的程序语言还有 Scilab 语言等.
算法案例
· 辗转相除法与更相减损术
辗转相除法是用于求两个正整数的最大公约数的一种算法,这种算法是由欧几里得在公元前 300 年左右首先提出的,因而又叫欧几里得算法.
更相减损术也可以用来求两个数的最大公约数,即“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也.以等数约之.”
· 秦九韶算法
把一个 n 次多项式 f(x)=anxn+an-1xn-1+⋯+a1x+a0 改写成如下形式:
f(x)=anxn+an-1xn-1+⋯+a1x+a0=(anxn-1+an-1xn-1+⋯+a1)x+a0=((anxn-2+an-1xn-3+⋯+a2)x+a1)x+a0=⋯=(⋯((anx+an-1)x+an-2)x+⋯+a1)x+a0.
求多项式的值时,首先计算内层括号内一次多项式的值,即 v1=anx+an-1,然后由内向外逐层计算一次多项式的值,即 v2=v1x+an-2,v3=v2x+an-3,⋯,vn=vn-1x+a0,这样,求 n 次多项式 f(x) 的值就转化为求 n 个一次多项式的值.这个方法称为秦九韶算法.
· 进位制
进位制是人们为了计数和运算方便而约定的计数系统.约定满二进一,就是二进制;满十进一,就是十进制;满十二进一,就是十二进制;“满几进一”就是几进制,几进制的基数就是几.
以 k 为基数的 k 进制数可以表示为一串数字连写在一起的形式:
anan-1⋯a1a0(k)
其中,an,an-1,⋯,a1,a0∈N,0
5,否,
x=3,y=5-2×3=-1,∣-1-3∣>5,否,
x=-1,y=5-2×-1=7,∣7--1∣>5,是,y=7.
4. 某算法流程图如图所示,则输出 k 的值是 .
【答案】 5
【分析】 模拟程序框图的运行过程,得;
k=1,S=10-1=9;
k=2,S=9-2=7;
k=3,S=7-3=4;
k=4,S=4-4=0;
S⩽0,输出 k=4+1=5.
5. 执行如图所示的程序框图,若输入 n 的值为 6,则输出 s 的值为 .
【答案】 15
6. 已知 n 个正整数排成一行,a1,a2,⋯,an.a1=1,a2=1,an=an-1+an-2,画出求 a100 的程序框图.
【解】 程序框图如图:
7. 根据程序框图(如图)回答下面问题,框图中 D 表示函数 fx 的定义域,fx=4x-2x+1.
(1)当 x 赋值 4965,N 赋值 10 时,执行程序框图所表示的程序,则当结束程序时,k= ,输出结果为 ;
【解】 4;1119,15,-1
(2)当 N 赋值 20 时,执行程序框图所表示的程序时,输出结果为相同的数值,则当结束程序时,k= ,x 应赋值为 .(写出所有可能结果)
【解】 21;1,2
8. 画出求使 1+2+3+⋯+n>2010 成立的最小自然数 n 的值的程序框图.
【解】 程序框图如下图
方法一:
方法二:
9. 根据下面 5 个程序框图,回答 1∼5 题.
(1)在程序框图(1),(2),(3),(4)中,只有顺序结构的程序框图是 ;
【解】 (1)
(2)在程序框图(1),(2),(3),(4)中,含循环结构的程序框图是 ;
【解】 (4)
(3)程序框图(2)对应的算法解决的问题是 ;
【解】 ∣a-b∣
(4)据程序框图(3),使输出的 y 值是 1,则输入的 x 值是 ;(写出所有可能的取值)
【解】 0,-1,1
(5)程序框图(4),(5)表示解决同一个问题的两种算法,根据程序框图(4),完成程序框图(5)中未写出的部分,① ;② ;③ .
【解】 S=0;i⩽6;i=i+1(答案不唯一)
10. 如图所示的程序框图,根据框图和各题的条件回答下面的问题:
(1)该框图解决的是一个什么问题?
【解】 该程序框图解决的是求二次函数 fx=-x2+mx 的函数值的问题.
(2)当输入的 x 值为 0 和 4 时,输出的值相等,问当输入的 x 值为 3 时,输出的 y 值为多少?
【解】 当输入的 x 值为 0 和 4 时,输出的值相等,即 f0=f4.
∵f0=0,f4=-16+4m,
∴-16+4m=0.
∴m=4.
∴fx=-x2+4x.
∵f3=-32+4×3=3,
∴ 输入的 x 值为 3 时,输出的 y 值为 3.
程序语句
1. 运行如图所示的伪代码,其结果为 .
S←1
For I From 1 To 7 step 2
S←S+I
End For
Print S
【答案】 17
2. 如图是一个算法的伪代码,运行后输出的 n 值为 .
n ← 5
S ← 0
WHILE S < 10
S ← S+n
n ← n-1
WEND
PRINT n
END
【答案】 2
3. 根据以下程序写出结果.
Input x
If x<10 Then
p=0.4x
Else
p=10×0.4+x-10×0.7
End if
Print p
End
(1)当 x=6 时,运行结果为 .
(2)当 x=20 时,运行结果为 .
【答案】 2.4;11
4. 如图所示程序的运行结果:s= ,n= .
n=1;s=0;
while s ≤ 25
s=s+n;
n=n+2;
end
print(%io(2),s,n)
【答案】 36;13
5. 阅读下列程序,回答问题:
i=1;
while i<8
i=i+3;
S=2i+3
i=i-1;
end
print(%io(2),S);
上述程序执行后,输出结果为 .
【答案】 23
6. 读下列两个程序回答问题:
①
x=3;
y=4;
x=y;
x
y
②
x=3;
y=4;
y=x;
x
y
(1)上述两个程序的运行结果分别是① ;② .
【解】 4,4;3,3
(2)上述两个程序的第三行有什么区别?
【解】 程序①中的第三行是将 y 的值赋给 x,赋值后 x 的值变为 4,y 的值不变;程序②中的第三行是将 x 的值赋给 y,赋值后 y 的值变为 3,x 的值不变.
7. 利用Scilab语言编写程序实现:“输入 a,b 两个数,比较两数大小,按 a 中存放最大值,b 中存放最小值输出.”
【解】 a=input(“b=”);
b=input(“a=”);
if a≤b
t=a;
a=b;
b=t;
end
print(% io(2),a,b);
8. 已知圆锥的底面半径和高,利用Scilab语言编写一个程序,求圆锥的体积.
【解】 r=input(“radius=’’);
h=input(“high=”);
S=%pi*r^2;
V=S*h/3;
print(%io(2),S)或者disp(S)或者S.
9. 试写出判断直线 Ax+By+C=0 与圆 x-a2+y-b2=r2r>0 的位置关系的算法.
【解】 第一步:输入圆心的坐标 a,b,直线方程的系数 A,B,C 和半径 r;
第二步:计算 z1=Aa+Bb+C;
第三步:计算 z2=A2+B2;
第四步:计算 d=|z1|z2;
第五步:如果 d>r,则直线与圆相离;如果 d=r,则直线与圆相切;如果 d<r,则直线与圆相交.
10. 已知圆锥的高及底面半径.利用Scilab语言编写一个程序,求圆锥的体积.
【解】 r=input(“radius=”);
h=input(“high=”);
S=%pi*r^2;
V=S*h/3;
print(%io(2),V);或者disp(V)
算法案例
1. 185 与 333 的最大公约数为 .
【答案】 37
2. 整数 459 与 357 的最大公约数是 .
【答案】 51
3. 两个数 90 , 252 的最大公约数是 .
【答案】 18
4. 三个数 144,240,336 的最大公约数是 .
【答案】 48
【分析】 求三个数的最大公约数时,可以先求其中两个数的最大公约数,然后再求这个最大公约数与第三个数的最大公约数,就是三个数的最大公约数.
5. 用秦九韶算法求多项式 fx=x6-5x5+6x4+x2+3x+2 的值,当 x=-2 时,v3 的值为
【答案】 -40
【分析】 fx=x-5x+6x+0x+xx+3x+2,则 v1=-7,v2=20,v3=-40.
(1)用辗转相除法求 840 与 1764 的最大公约数.
【解】 1764=840×2+84,
840=84×10+0,
所以 840 与 1764 的最大公约数为 84.
(2)用更相减损术求 561 与 255 的最大公约数.
【解】 561-255=306,
306-255=51,
255-51=204,
204-51=153,
153-51=102,
102-51=51,
所以 561 与 255 的最大公约数为 51.
7. 已知函数 fx=x3-2x2-5x+6,用秦九韶算法求 f10 的值.
【解】 根据秦九韶算法,我们可以简化成下面的形式:
fx=x3-2x2-5x+6=x2-2x-5x+6=x-2x-5x+6.
把 x=10 代入函数式,f10=10-2×10-5×10+6=756.
8. 已知一个 5 次多项式函数为 fx=5x5+2x4+3.5x3-2.6x2+1.7x-0.8,用秦九韶算法求这个多项式当 x=5 时的值.
【解】 可根据秦九韶算法原理,先将所给的多项式进行改写.然后由内向外逐次计算即可.
fx=5x5+2x4+3.5x3-2.6x2+1.7x-0.8=5x+2x+3.5x-2.6x+1.7x-0.8.
v0=5,v1=5×5+2=27,v2=27×5+3.5=138.5,v3=138.5×5-2.6=689.9,v4=689.9×5+1.7=3451.2,
v5=3451.2×5-0.8=17255.2.
所以,当 x=5 时,多项式的值等于 17255.2.
9. 用更相减损术求 288 和 123 的最大公约数.
【解】 288-123=165,
165-123=42,
123-42=81,
81-42=39,
42-39=3,
39-3=36,
36-3=33,
33-3=30,
30-3=27,
27-3=24,
24-3=21,
21-3=18,
18-3=15,
15-3=12,
12-3=9,
9-3=6,
6-3=3.
故 288 和 123 的最大公约数是 3.
10. 分别用辗转相除法与更相减损术求 27090 与 8127 的最大公约数,并且由此比较这两种算法.
【解】 更相减损术:
27090,8127→8127,18963→8127,10836→8127,2709→2709,5418→2709,2709
故它们的最大公约数为 2709 .
辗转相除法:
27090=8127×3+2709 , 8127=2709×3 ;
故它们的最大公约数为 2709 .
联系:都是求最大公约数的方法;
区别:①计算上辗转相除法以除法为主,更相减损术以减法为主;
②计算次数上,辗转相除法计算次数相对较少,特别是当两个数差别较大时区别明显;
③从结果输出的时候看,辗转相除法当"余数为 0 "时输出"除数",更相减损术当"差和减数相等"时输出"差".
流程图
1. 李强用流程图把早上上班前需要做的事情做了如下几种方案,则所用时间最少的方案是 .
【答案】 方案三
2. 下面算法流程图的功能是"输入两个数,输出这两个数差的绝对值",则①②处分别填:
① ;② .
【答案】 ① a⩾b(或 a>b);② b-a
3. 某工厂加工某种零件的工序流程图:
按照这个工序流程图,一件成品至少经过 道加工和检验.
【答案】 2
4. 下图是一个程序操作流程图:按照这个工序流程图,一件成品最多经过 道加工和检验程序,导致废品的产生有 种不同的情形.
【答案】 6;3
【分析】 (1) 最多经过 " 粗加工 "、" 检验 "、" 返修加工 "、" 返修检验 "、" 精加工 "、" 最后检验 " 六道加工和检验程序.
(2) 三种不同情形:
① 返修检验不合格;
② 检验合格→精加工 → 最后检验不合格;
③ 返修检验合格→精加工 → 最后检验不合格.
5. 由一些 构成的图示,称为流程图,流程图常常用来表示一些 过程,通常会有一个起点,一个或多个终点.
【答案】 图形符号和文字符号;动态
6. 设计流程图,描述判断函数 fx 是否是偶函数的过程.
【解】 如图.
7. 设计流程图,描述处理算法中循环结构的过程.
【解】 如图.
8. 已知椭圆 c:x2a2+y2b2a>b>0 的离心率为 33,过右焦点 F 的直线 l 与椭圆 C 相交于 A,B 两点,当 l 的斜率为 1 时,坐标原点 O 到 l 的距离为 23.求 a,b 的值.设计流程图,描述 a,b 的求解过程.
【解】 如图.
9. 请画出你从写信到发信的全过程的流程图.
【解】
10. 函数 y=-x+1,x>0,0,x=0,x+3,x<0. 请设计算法流程图,要求输入自变量的值,输出函数值.
【答案】
【解】
结构图
1. 结构图一般由构成系统的 和表达各要素之间的关系的连线构成,连线通常按照 的方向表示要素的从属关系或逻辑的先后关系.
【答案】 若干要素;从左到右、从上到下
2. 一般情况下,下位要素比上位要素更为 ,上位要素比下位要素更为 ,下位要素越多,结构图越 .
【答案】 具体; 抽象; 复杂
3. 按边对三角形进行分类的结构图,则①处应填入 .
【答案】 等边三角形
4. 在工商管理学中,MRP(Material Requirement Plan-ning)指的是物资需求计划,基本MRP的体系结构如图所示.从图中可以看出,主生产计划受 和 的影响.
【答案】 用户订单;需求预测
5. 用结构图来描述《必修三》第二章“统计”的知识结构.
【解】 如图.
6. 有下列要素:糖、盐、碱、有机物、物质、醋、无机物、酒精,设计一个结构图表示这些要素及其关系.
【解】
7. 某公司局域网设置如下:由服务器联结经理室,市场部,销售部,客户服务部,系统管理员,与外部联结是通过服务器,试画出该公司局域网设置结构图.
【解】
8. 通过我们对角的认识及学习,试分析用树形结构图和网状结构图将其分类表示出来.
【解】 树形结构图如图1所示.
网状结构如图2所示.
9. 某公司做人事调整:设总经理一名,配有经理助理一名;设副总经理两人,直接对总经理负责,设有 6 个部门,其中副总经理 A 管理生产部、安全部和质量部,副总经理 B 管理销售部、财务部和保卫部;生产车间由生产部和安全部共同管理,公司配有质检中心和门岗,分别隶属质量部和保卫部领导.请根据以上信息设计并画出该公司的人事结构图.
【解】
课后练习
1. “判断整数 n(n>2)是否为质数”的算法可以按如下步骤进行:
S1 给定大于 2 的整数 n.
S2 令 i=2.
S3 用 i 除 n,得到余数 r.
S4 判断余数 r 是否为 0.若为 0,则不是质数,结束算法;否则将 i 的值增加 1 仍用 i 表示.
S5 判断 i 是否大于 n-1.若是,则是质数,结束算法;否则返回第三步.
现设给定的整数为 35,则算法结束时 i 的值是 .
2. 程序设计语言一般包含 、 、 、 、 五种基本算法语句.
3. 运算速度快是计算机一个很重要的特点,而算法好坏的一个重要标志是 .
4. 完成不等式 2x+3<3x+2 的算法过程:
(1)将含 x 的项移项至不等式的左边,将常数项移至不等式的右边,得 ;
(2)在不等式两边同时除以 x 的系数,得 .
5. 用冒泡排序法从小到大排列数据 13,5,9,10,7,4 ,需要经过 趟排序才能完成.
6. 在如图所示的流程图中,该程序运动后输出的 i 的值是 .
7. 如图,函数 fx=2x,gx=x2,若输入的 x 值为 3,则输出的 hx 的值为 .
8. 如图给出的是计算 S=1+12+13+⋯+1n 值的一个程序框图,当程序结束时,n 的值为 .
9. 阅读下面两个程序框图,框图(1)输出的结果为 ;框图(2)输出的结果为 .
10. 如图是求 12+22+32+⋯+1002 的值的程序框图,则正整数 n= .
11. 阅读下列程序,回答问题:
j=0;
for i=1:3:46
if i>15
j=j+1;
end
end
print(%io(2),j);
上述程序执行后,输出结果为 .
12. 把下面程序补充完整,使得当执行此程序时,输入 a,b 的值,输出的值满足下列要求:
(1)输入 a=3,b=2,输出 4;
(2)输入 a=3,b=3,输出 3;
(3)输入 a=3,b=4,输出 4.
① ;
② ;
③if ;
④ ;
else
a=b^2
end
a
注:所填各条语句写出一种可能的方案即可,空格③要求填入的是输入值 a,b 的大小比较.
13. 下面给出了一个问题的算法:
S1:输入 a;
S2:若 a⩾2,则执行 S3,否则执行 S4;
S3:输出 2a-1;
S4:输出 a2-2a.
根据上面算法,对任意实数 q 值的输入,输出值的最小值是 ,此时输入 a= .
14. 依据如图给出的算法代码,运行后输出的结果为 .
a←1
S←0
While a⩽4
S←S+a2
a←a+1
End While
Print S
15. 写出下列语句的运行结果:
输入 a
if a<0
then 输出“是负数”
else t=a
输出 t
当 a=-4 时,输出的结果为 ,当 a=9 时,输出的结果为 .
16. 用辗转相除法求得 228 与 1995 的最大公约数为: .
17. 进位制转化:1011012= 5.
18. 完成下列进位制之间的转化:102103= 10;13134= 6.
19. 下列各数 859 、 2106 、 1111112 中最大的数是 .
20. 下列各数 859 、 2106 、 10004 、 1111112 中最小的数是 .
21. 某工程的工序流程图如图(工时单位:天).现已知工程总时数为 10 天,则工序 c 所需工时为 天.
22. 流程图中的判断框有 1 个入口和 个出口.
23. 流程图中两相邻工序之间用 连接.
24. 如图所示的流程图是交换两个变量的值并输出,则图中空白处应为 .
25. 某算法流程图如图所示,若输入 a=2,b=1,则输出的值为 .
26. 一位商人有 9 枚银元,其中 1 枚略轻的是假银元.你能用天平(不用砝码)将假银元找出来吗?试设计一个算法.
27. 现在有三个油瓶,分别能装 8 kg 、 5 kg 、 3 kg 的油,当 8 kg 的瓶子装满油时,设计一个用这三个瓶子倒油的算法,怎样倒能使这些油被平分到两个瓶子里.(注:没有其它瓶子)
28. 任意给定一个大于 1 的正整数 n,设计一个算法求出 n 的所有因数.
29. 下面给出一个问题的算法:
第一步,输入 x;
第二步,若 x⩾4,则执行第三步,否则执行第四步;
第三步,输出 2x-1 结束;
第四步,输出 x2-2x+3 结束.
问:
(1)这个算法解决的问题是什么?
(2)当输入的 x 的值为多少时,输出的数值最小?
30. 下面给出了一个问题的算法:
第一步:输入 a;
第二步:若 a⩾4,则执行第三步,否则执行第四步;
第三步:输出 2a-1;
第四步:输出 a2-2a+3.
问题:
(1)这个算法解决的问题是什么?
(2)当输入的 a 值为多大时,输出的数值最小?
31. 给定实数 a,函数 fx=lnx,用程序框图画出求 fa 的一个算法.
32. 计算 1×3×5×⋯×99 的值,画出程序框图,写出程序.
33. 如图所示的程序框图中,已知 fx=3x+5x-1 的定义域为 D.
(1)若输入的 x0=-75,求输出的所有的 xi;
(2)若输出的所有的 xi 都相等,求输入的 x0 的值.
34. 画出求 12+22+…+992+1002 的值的算法的程序框图.
35. 国家法定工作日内,每周工作时间满工作量为 40 小时,每小时工资 8 元;如因需要加班,则每小时工资为 10 元,某人在一周内工作时间为 x 小时,个人住房公积金、失业险等合计为 10%.试写出其净得工资 y 元的算法的程序框图.
(1)利用Scilab语言编写程序,计算 12+22+⋯+1002 的值;
(2)利用Scilab语言编写程序,求使 12+22+⋯+n2<1000 成立的最大自然数 n 值.
37. 已知 S=12-22+32-42+⋯⋯+n-12-n2,
(1)请设计程序框图,算法要求从键盘输入偶数 n,输出 S.
(2)并写出计算机程序语言.
(3)当 n=100 时,求 S 的值.
38. 已知函数 y=2,x>21,14 时,计算 y=x+2;否则执行下一步.
第三步,计算 y=4-x.
第四步,输出 y.
当输入 x=0 时,输出 y= .
5. 算法:
S1:输入x,y
S2:m=max{x,y}
S3:n=min{x,y}
S4:若m/n=[m/n]([x]表示x的整数部分),则输出n,否则执行S5
S5:r=m-[m/n]*n
S6:m=n
S7:n=r
S8:执行S4
S9:输出n
上述算法的含义是 .
6. 如图是一个算法的流程图,最后输出的 n 值为 .
7. 阅读如图所示的程序框图,运行相应的程序,输出的结果 s= .
8. 阅读如图所示的程序框图,运行相应的程序,输出的 s 值等于 .
9. 2010 年上海世博会园区每天 9:00 开园,20:00 停止入园.在下边的框图中,S 表示上海世博会官方网站在每个整点报道的入园总人数,a 表示整点报道前 1 个小时内入园人数,则空白的执行框内应填入 .
10. 如图是一个算法的流程图,则输出的 n 的值是 .
11. 下面给出了一个问题的算法:
根据上面的算法,对任意实数 a 值的输入,输出值的最小值为 ,此时输入 a= .
12. 根据所给程序pro-1回答问题:
a=input("a=");
y=3a+1;
a=y;
y=3a+1;
print(% io(2),y);
完成下面程序pro-2设计,使之与程序pro-1功能相同
a=input("a=");
1 ;
2 ;
print(%io(2),y).
13. Read a,b
If a>b Then
m←a
Else
m←b
End If
Print m
根据上述伪代码,当输入 a,b 分别为 2,3 时,最后输出的 m 的值是 .
14. 根据所给程序pro-1回答问题:
a=input("a=");
y=3a+1;
a=y;
y=3a+1;
print(% io(2),y);
当 a 赋值 3 时,输出 y 值为 .
15. 执行如图所示的伪代码,则输出的结果为 .
I←1
While I<7
S←2I+1
I←I+2
End While
Print S
16. 完成进位制之间的转化: 1206 = 2 .
17. 用秦九韶算法计算多项式 fx=6x5+5x4+4x3+3x2+2x+1 当 x=2 时的值的过程中,要经过 次乘法运算和 次加法运算;若直接计算,要经过 次乘法运算和 次加法运算.
18. 已知一个 k 进制数 132 与十进制数 30 相等,那么 k= .
19. 我国古代数学发展一直处于世界领先水平,特别是宋、元时期的"算法",其中可以同欧几里德辗转相除法相媲美的是 .
20. 228 与 1995 的最大公约数是 .
21. 一般来说,一个复杂的流程图都可以分解成 、 、 三种结构;
22. 坐标法是解析几何的基本方法,研究曲线性质的过程是:建立坐标系求曲线方程,由曲线方程研究曲线性质,这一过程的流程图是 .
23. 为确保信息安全,信息需加密传输,发送方由明文 → 密文(加密),接收方由密文 → 明文(解密).已知加密规则如图所示,例如,明文 1,2,3,4 对应密文 5,7,18,16,当接收方收到密文 14,9,23,28 时,则解密得到的明文为 .
24. 流程图和结构图都是按照 , 的顺序绘制,流程图只有 起点, 终点.
25. 已知一个正三角形的周长为 a,求这个正三角形的面积.设计一个算法解决这个问题.
26. 给出一个判断点 Px0,y0 是否在直线 y=x-1 上的一个算法.
27. 设计一个算法,求 459 与 306 的最大公约数.
28. 设计一个算法求解方程组 3x+y=7,4x+5y=13.
29. 写出计算 1×2×3×⋯×9×10 的值的一个算法.
30. 画出求 5+15+15+15+15+15+15 的值的算法的程序框图.
31. 写出 x=2 时,求函数 y=x2-2x 的函数值的一个算法,并用程序框图表示.
32. 求平方值小于 2000 的最大整数,画出程序框图.
33. 根据下面计算 2+4+6+⋯+100 的值的算法,画出程序框图.
算法如下:
S1 使 p=2
S2 使 i=4
S3 使 p=p+i
S4 使 i=i+2
S5 若 i⩽100,则返回步骤 S3 继续执行;否则输出 p 的值,算法结束.
34. 如果我国工业总产值以每年 9% 的增长率增长,问几年后,我国工业总产值翻一番?试用程序框图描述该问题的算法.
35. 读下列两个程序回答问题:
(1)上述两个程序的运行结果分别是 ① ;② .
(2)上述两个程序的第三行有什么区别?
36. 利用Scilab语言编写程序实现:“输人 a,b 两个数,比较两值,按 a 中存放较大值,b 中存放较小值输出”.
37. 假定在银行中存款 10000 元,按 1.125% 的利率一年后连本带利将变为 10112.5 元,若将此款继续存入银行,试问多长时间就会连本带利翻一番?请用直到型和当型两种语句写出程序.
38. 编写程序:求 x2-1,2x-3,-x2+2x,-x2-x 中的最小者.
39. 某城市现有人口总数为 100 万人,如果年自然增长率为 1.2%,试解答下列问题:
(1)写出该城市人口数 y(万人)与年份 x(年)的函数关系式;
(2)编写表示计算 10 年后该城市人口总数的程序;
(3)编写程序:计算大约多少年以后该城市人口将达到 120 万人.
40. 甲,乙,丙三种溶液的质量分别为 147 g,343 g,133 g,现要将它们分别全部装入小瓶中,每个小瓶中装入溶液的质量相同,问每瓶最多装多少?
41. 用秦九韶算法写出求 fx=1+x+0.5x2+0.16667x3+0.04167x4+0.00833x5 在 x=-0.2 时的值的过程.
42. 用等值算法求三个数 168,56,264 的最大公约数.
43. 计算下列问题:
(1)用辗转相除法求 840 与 1764 的最大公约数.
(2)用秦九韶算法计算函数 fx=2x4+3x3+5x-4 当 x=2 时的函数值.
44. 用秦九韶算法计算多项式 fx=x6-12x5+60x4-160x3+240x2-192x+64,当 x=2 时的值.
45. 已知三个实数 a,b,c,试给出寻找这三个数中最大数的一个算法,并画出该算法的流程图.