数学卷·2018届湖南省张家界市民族中学高二上学期期中数学试卷（理科）（解析版）

数学卷·2018届湖南省张家界市民族中学高二上学期期中数学试卷（理科）（解析版）

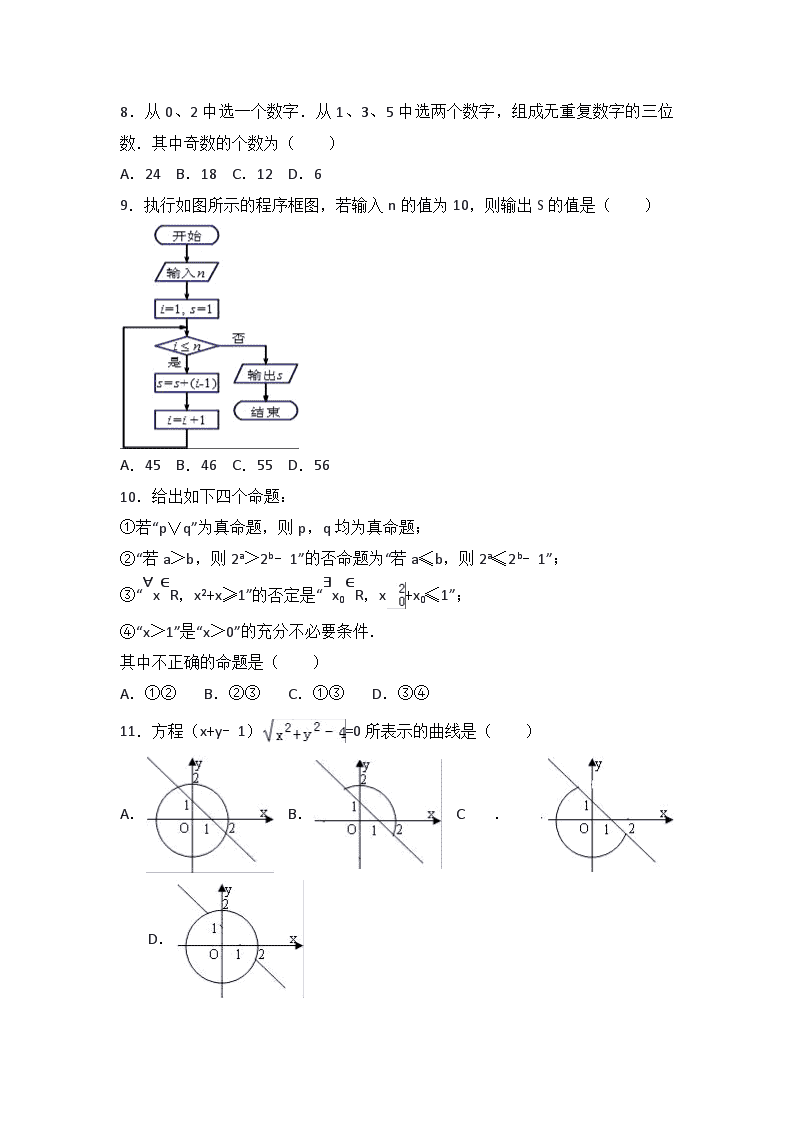
‎2016-2017学年湖南省张家界市民族中学高二（上）期中数学试卷（理科）‎ ‎　‎ 一、选择题（共12小题，每小题5分，满分60分）‎ ‎1．设随机变量ξ服从标准正态分布N（0，1），在某项测量中，已知p（|ξ|＜1.96=0.950，则ξ在（﹣∞，﹣1.96）内取值的概率为（　　）‎ A．0.025 B．0.050 C．0.950 D．0.975‎ ‎2．已知一个线性回归方程为=1.5x+45，其中x的取值依次为1，7，5，13，19，则=（　　）‎ A．58.5 B．46.5 C．60 D．75‎ ‎3．设a∈R，则a＞1是＜1的（　　）‎ A．必要但不充分条件 B．充分但不必要条件 C．充要条件 D．既不充分也不必要条件 ‎4．已知函数f（x）=x5+2x4+x3﹣x2+3x﹣5，用秦九韶算法计算，当x=5时，V3=（　　）‎ A．27 B．36 C．54 D．179‎ ‎5．某班50人的一次竞赛成绩的频数分布如下：[60，70）：3人，[70，80）：16人，[80，90）：24人，[90，100]：7人，利用各组区间中点值，可估计本次比赛该班的平均分为（　　）‎ A．56 B．68 C．78 D．82‎ ‎6．若一个椭圆的内接正方形有两边分别经过它的两个焦点，则此椭圆的离心率为（　　）‎ A． B． C． D．‎ ‎7．通讯中常采取重复发送信号的办法来减少在接收中可能发生的错误，假定接收一个信号时发生错误的概率是，为减少错误，采取每一个信号连发3次，接收时以“少数服从多数”的原则判断，则判错一个信号的概率为（　　）‎ A． B． C． D．‎ ‎8．从0、2中选一个数字．从1、3、5中选两个数字，组成无重复数字的三位数．其中奇数的个数为（　　）‎ A．24 B．18 C．12 D．6‎ ‎9．执行如图所示的程序框图，若输入n的值为10，则输出S的值是（　　）‎ A．45 B．46 C．55 D．56‎ ‎10．给出如下四个命题：‎ ‎①若“p∨q”为真命题，则p，q均为真命题；‎ ‎②“若a＞b，则2a＞2b﹣1”的否命题为“若a≤b，则2a≤2b﹣1”；‎ ‎③“∀x∈R，x2+x≥1”的否定是“∃x0∈R，x+x0≤1”；‎ ‎④“x＞1”是“x＞0”的充分不必要条件．‎ 其中不正确的命题是（　　）‎ A．①② B．②③ C．①③ D．③④‎ ‎11．方程（x+y﹣1）=0所表示的曲线是（　　）‎ A． B． C． D．‎ ‎12．从双曲线=1（a＞0，b＞0）的左焦点F引圆x2+y2=a2的切线，切点为T，延长FT交双曲线右支于点P，若M为线段FP的中点，O为坐标原点，则|MO|﹣|MT|与b﹣a的大小关系为（　　）‎ A．|MO|﹣|MT|＞b﹣a B．|MO|﹣|MT|=b﹣a C．|MP|﹣|MT|＜b﹣a D．不确定 ‎　‎ 二、填空题（本大题共4小题，每小题5分，共20分.请把答案填写在答题卡上）‎ ‎13．已知（﹣）n的展开式中只有第四项的二项式系数最大，则展开式中的常数项等于　　．‎ ‎14．在直角坐标系xOy中，设集合Ω={（x，y）|0≤x≤2，0≤y≤1}，在区域Ω内任取一点P（x，y），则满足x+y≥1的概率是　　．‎ ‎15．一个圆经过椭圆=1的三个顶点．且圆心在x轴的正半轴上．则该圆标准方程为　　．‎ ‎16．已知命题p：“函数在R上有零点”，命题q：函数f（x）=在区间（1，+∞）内是减函数，若p∧q为真命题，则实数m的取值范围为　　．‎ ‎　‎ 三、解答题（本大题共6小题，共70分，要求写出必要的文字说明、证明过程和演算步骤）‎ ‎17．已知a为实数，p：点M（1，1）在圆（x+a）2+（y﹣a）2=4的内部； q：∀x∈R，都有x2+ax+1≥0．‎ ‎（1）若p为真命题，求a的取值范围；‎ ‎（2）若q为假命题，求a的取值范围；‎ ‎（3）若“p且q”为假命题，且“p或q”为真命题，求a的取值范围．‎ ‎18．已知椭圆，动直线 ‎（1）若动直线l与椭圆C相交，求实数m的取值范围；‎ ‎（2）当动直线l与椭圆C相交时，证明：这些直线被椭圆截得的线段的中点都在直线3x+2y=0上．‎ ‎19．4月23人是“世界读书日”，某中学在此期间开展了一系列的读书教育活动，为了解本校学生课外阅读情况，学校随机抽取了100名学生对其课外阅读时间进行调查，下面是根据调查结果绘制的学生日均课外阅读时间（单位：分钟）的频率分布直方图，若将日均课外阅读时间不低于60分钟的学生称为“读书谜”，低于60分钟的学生称为“非读书谜”‎ ‎（1）根据已知条件完成下面2×2的列联表，并据此判断是否有99%的把握认为“读书谜”与性别有关？‎ 非读书迷 读书迷 合计 男 ‎15‎ 女 ‎45‎ 合计 ‎（2）将频率视为概率，现在从该校大量学生中，用随机抽样的方法每次抽取1人，共抽取3次，记被抽取的3人中的“读书谜”的人数为X，若每次抽取的结果是相互独立的，求X的分布列，期望E（X）和方程D（X）‎ 附：K2=n=a+b+c+d P（K2≥k0）‎ ‎0.100‎ ‎0.050‎ ‎0.025‎ ‎0.010‎ ‎0.001‎ k0‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎10.828‎ ‎20．在奥运会射箭决赛中，参赛号码为1～4号的4名射箭运动员参加射箭比赛．‎ ‎（1）通过抽签将他们安排到1～‎ ‎4号靶位，试求恰有2名运动员所抽靶位号与其参赛号码相同的概率；‎ ‎（2）记1号、2号射箭运动员射箭的环数为ξ（ξ所有取值为0，1，2，3，…，10）分别为P1，P2．根据教练员提供的资料，其概率分布如下表：‎ ξ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ P1‎ ‎0‎ ‎0‎ ‎0‎ ‎0‎ ‎0.06‎ ‎0.04‎ ‎0.06‎ ‎0.3‎ ‎0.2‎ ‎0.3‎ ‎0.04‎ P2‎ ‎0‎ ‎0‎ ‎0‎ ‎0‎ ‎0.04‎ ‎0.05‎ ‎0.05‎ ‎0.2‎ ‎0.32‎ ‎0.32‎ ‎0.02‎ ‎①若1，2号运动员各射箭一次，求两人中至少有一人命中9环的概率；‎ ‎②判断1号、2号射箭运动员谁射箭的水平高？并说明理由．‎ ‎21．已知曲线x2+y=8与x轴交于A，B两点，动点P与A，B连线的斜率之积为．‎ ‎（1）求动点P的轨迹C的方程．‎ ‎（2）MN是动点P轨迹C的一条弦，且直线OM，ON的斜率之积为．求的最小值．‎ ‎22．已知椭圆C：的离心率，且过点Q ‎（1）求椭圆C的方程．‎ ‎（2）椭圆C长轴两端点分别为A，B，点P为椭圆上异于A，B的动点，定直线x=4与直线PA，PB分别交于M，N两点，直线PA，PB的斜率分别为k1，k2‎ ‎①证明；‎ ‎②若E（7，0），过E，M，N三点的圆是否过x轴上不同于点E的定点？若经过，求出定点坐标；若不经过，请说明理由．‎ ‎　‎ ‎2016-2017学年湖南省张家界市民族中学高二（上）期中数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题（共12小题，每小题5分，满分60分）‎ ‎1．设随机变量ξ服从标准正态分布N（0，1），在某项测量中，已知p（|ξ|＜1.96=0.950，则ξ在（﹣∞，﹣1.96）内取值的概率为（　　）‎ A．0.025 B．0.050 C．0.950 D．0.975‎ ‎【考点】正态分布曲线的特点及曲线所表示的意义．‎ ‎【分析】根据随机变量ξ服从标准正态分布N（0，1），得到正态曲线关于x=0对称，ξ在（﹣∞，1.96）内取值的概率为所给的范围外的概率的一半．‎ ‎【解答】解：∵随机变量ξ服从标准正态分布N（0，1），‎ 正态曲线关于x=0对称，‎ P（|ξ|＜1.96）=0.950，‎ ‎∴ξ在（﹣∞，1.96）内取值的概率为（1+0.950）=0.975‎ 故选D．‎ ‎　‎ ‎2．已知一个线性回归方程为=1.5x+45，其中x的取值依次为1，7，5，13，19，则=（　　）‎ A．58.5 B．46.5 C．60 D．75‎ ‎【考点】线性回归方程．‎ ‎【分析】根据所给的x的值，求出x的平均数，根据样本中心点在线性回归直线上，把所求的平均数代入线性回归方程，求出y的平均数．‎ ‎【解答】解：∵x∈{1，7，5，13，19}，‎ ‎∴==9，‎ ‎∴=1.5×9+45=58.5．‎ 故选：A．‎ ‎　‎ ‎3．设a∈R，则a＞1是＜1的（　　）‎ A．必要但不充分条件 B．充分但不必要条件 C．充要条件 D．既不充分也不必要条件 ‎【考点】不等关系与不等式；充要条件．‎ ‎【分析】根据 由a＞1，一定能得到＜1．但当＜1时，不能推出a＞1 （如 a=﹣1时），从而得到结论．‎ ‎【解答】解：由a＞1，一定能得到＜1．但当＜1时，不能推出a＞1 （如 a=﹣1时），‎ 故a＞1是＜1 的充分不必要条件，‎ 故选 B．‎ ‎　‎ ‎4．已知函数f（x）=x5+2x4+x3﹣x2+3x﹣5，用秦九韶算法计算，当x=5时，V3=（　　）‎ A．27 B．36 C．54 D．179‎ ‎【考点】秦九韶算法．‎ ‎【分析】利用秦九韶算法计算多项式的值，先将多项式转化为f（x）=5x5+4x4+3x3+2x2+x=（（（（5x+4）x+3）x+2）x+1）x的形式，然后求解即可．‎ ‎【解答】解：f（x）=x5+2x4+x3﹣x2+3x﹣5=（（（（x+2）x+1）x﹣1）x+3）x﹣5‎ 则当x=5时，V0=1，V1=5+2=7，V2=35+1=36，V3=180﹣1=179．‎ 故选D．‎ ‎　‎ ‎5．某班50人的一次竞赛成绩的频数分布如下：[60，70）：3人，[70，80）：16人，[80，90）：24人，[90，100]：7人，利用各组区间中点值，可估计本次比赛该班的平均分为（　　）‎ A．56 B．68 C．78 D．82‎ ‎【考点】众数、中位数、平均数．‎ ‎【分析】由已知条件，利用平均数公式计算即可．‎ ‎【解答】解：某班50人的一次竞赛成绩的频数分布如下：[60，70）：3人，[70，80）：16人，[80，90）：24人，[90，100]：7人，‎ 利用组中值可估计本次比赛该班的平均分为：‎ ‎=×（65×3+75×16+85×24+95×7）=82．‎ 故选：D．‎ ‎　‎ ‎6．若一个椭圆的内接正方形有两边分别经过它的两个焦点，则此椭圆的离心率为（　　）‎ A． B． C． D．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】由题意可知：椭圆的通径长，则=2c，由椭圆的离心率e=，求得e2+e﹣1=0，根据椭圆的离心率取值范围，即可求得椭圆的离心率．‎ ‎【解答】解：假设椭圆的焦点在x轴上，设椭圆的方程为：（a＞b＞0），‎ 由椭圆与正方形的对称性可知：正方形的一边长为椭圆焦距为2c，‎ 另一边长为通径长，‎ 则=2c，‎ ‎∴a2﹣c2=ac，由椭圆的离心率e=，‎ 整理得：e2+e﹣1=0，‎ 解得：e=，‎ 由椭圆的离心率e＞0，‎ 则e=，‎ 故选C．‎ ‎　‎ ‎7．通讯中常采取重复发送信号的办法来减少在接收中可能发生的错误，假定接收一个信号时发生错误的概率是，为减少错误，采取每一个信号连发3次，接收时以“少数服从多数”的原则判断，则判错一个信号的概率为（　　）‎ A． B． C． D．‎ ‎【考点】n次独立重复试验中恰好发生k次的概率．‎ ‎【分析】得到正确信号的概率有两种情形，一种情形是三次正确，另一种情形是两次正确一次不正确，分别求出相应的概率，然后利用对立事件的概率公式求出判错一个信号的概率即可．‎ ‎【解答】解：得到正确信号的概率有两种情形，一种情形是三次正确，概率为=‎ 另一种情形是两次正确，一次不正确，概率为=‎ ‎∴判错一个信号的概率为1﹣﹣=‎ 故选B．‎ ‎　‎ ‎8．从0、2中选一个数字．从1、3、5中选两个数字，组成无重复数字的三位数．其中奇数的个数为（　　）‎ A．24 B．18 C．12 D．6‎ ‎【考点】计数原理的应用．‎ ‎【分析】分类讨论：从0、2中选一个数字0，则0只能排在十位；从0、2中选一个数字2，则2排在十位或百位，由此可得结论．‎ ‎【解答】解：从0、2中选一个数字0，则0只能排在十位，从1、3、5中选两个数字排在个位与百位，共有=6种；‎ 从0、2中选一个数字2，则2排在十位，从1、3、5中选两个数字排在个位与百位，共有=6种；‎ ‎2排在百位，从1、3、5中选两个数字排在个位与十位，共有=6种；‎ 故共有3=18种 故选B．‎ ‎　‎ ‎9．执行如图所示的程序框图，若输入n的值为10，则输出S的值是（　　）‎ A．45 B．46 C．55 D．56‎ ‎【考点】程序框图．‎ ‎【分析】模拟执行程序框图，依次写出每次循环得到的S，i的值，当i=11时不满足条件i≤10，退出循环，输出S的值为46，从而得解．‎ ‎【解答】解：模拟执行程序，可得 n=10，i=1，s=1‎ 满足条件i≤10，执行循环体，s=1，i=2‎ 满足条件i≤10，执行循环体，s=2，i=3‎ 满足条件i≤10，执行循环体，s=4，i=4‎ 满足条件i≤10，执行循环体，s=7，i=5‎ 满足条件i≤10，执行循环体，s=11，i=6‎ 满足条件i≤10，执行循环体，s=16，i=7‎ 满足条件i≤10，执行循环体，s=22，i=8‎ 满足条件i≤10，执行循环体，s=29，i=9‎ 满足条件i≤10，执行循环体，s=37，i=10‎ 满足条件i≤10，执行循环体，s=46，i=11‎ 不满足条件i≤10，退出循环，输出s的值为46．‎ 故选：B．‎ ‎　‎ ‎10．给出如下四个命题：‎ ‎①若“p∨q”为真命题，则p，q均为真命题；‎ ‎②“若a＞b，则2a＞2b﹣1”的否命题为“若a≤b，则2a≤2b﹣1”；‎ ‎③“∀x∈R，x2+x≥1”的否定是“∃x0∈R，x+x0≤1”；‎ ‎④“x＞1”是“x＞0”的充分不必要条件．‎ 其中不正确的命题是（　　）‎ A．①② B．②③ C．①③ D．③④‎ ‎【考点】命题的真假判断与应用．‎ ‎【分析】①根据复合命题真假关系进行判断，‎ ‎②根据否命题的定义进行判断，‎ ‎③根据全称命题的否定是特称命题进行判断即可，‎ ‎④根据充分条件和必要条件的定义进行判断．‎ ‎【解答】解：①若“p∨q”为真命题，则p，q至少有一个是真命题，故①错误；‎ ‎②“若a＞b，则2a＞2b﹣1”的否命题为“若a≤b，则2a≤2b﹣1”，故②正确，‎ ‎③“∀x∈R，x2+x≥1”的否定是“∃x0∈R，x+x0＜1”；故③错误，‎ ‎④若x＞1，则x＞0成立，即充分性成立，‎ 若当x=满足x＞0，但x＞1不成立，即x＞0“x＞1”是“x＜0”的充分不必要条件．故④正确，‎ 故错误的是①③，‎ 故选：C．‎ ‎　‎ ‎11．方程（x+y﹣1）=0所表示的曲线是（　　）‎ A． B． C． D．‎ ‎【考点】曲线与方程．‎ ‎【分析】原方程等价于：，或x2+y2=4；两组方程分别表示出圆和不在圆内部分的直线，进而可推断出方程表示的曲线为圆和与圆相交且去掉圆内的部分．‎ ‎【解答】解：原方程等价于：，或x2+y2=4；其中当x+y﹣1=0需有意义，等式才成立，即x2+y2≥4，此时它表示直线x﹣y﹣1=0上不在圆x2+y2=4内的部分，这是极易出错的一个环节．‎ 故选D ‎　‎ ‎12．从双曲线=1（a＞0，b＞0）的左焦点F引圆x2+y2=a2的切线，切点为T，延长FT交双曲线右支于点P，若M为线段FP的中点，O为坐标原点，则|MO|﹣|MT|与b﹣a的大小关系为（　　）‎ A．|MO|﹣|MT|＞b﹣a B．|MO|﹣|MT|=b﹣a C．|MP|﹣|MT|＜b﹣a D．不确定 ‎【考点】双曲线的简单性质．‎ ‎【分析】将点P置于第一象限．设F1是双曲线的右焦点，连接PF1．由M、O分别为FP、FF1的中点，知|MO|=|PF1|．由双曲线定义，知|PF|﹣|PF1|=2a，|FT|==b．由此知|MO|﹣|MT|=（|PF1|﹣|PF|）+|FT|=b﹣a．‎ ‎【解答】解：将点P置于第一象限．‎ 设F1是双曲线的右焦点，连接PF1‎ ‎∵M、O分别为FP、FF1的中点，∴|MO|=|PF1|．‎ 又由双曲线定义得，‎ ‎|PF|﹣|PF1|=2a，‎ ‎|FT|==b．‎ 故|MO|﹣|MT|‎ ‎=|PF1|﹣|MF|+|FT|‎ ‎=（|PF1|﹣|PF|）+|FT|‎ ‎=b﹣a．‎ 故选：B．‎ ‎　‎ 二、填空题（本大题共4小题，每小题5分，共20分.请把答案填写在答题卡上）‎ ‎13．已知（﹣）n的展开式中只有第四项的二项式系数最大，则展开式中的常数项等于　15　．‎ ‎【考点】二项式系数的性质．‎ ‎【分析】先利用展开式中只有第四项的二项式系数最大求出n=6，再求出其通项公式，令x的指数为0，求出r，再代入通项公式即可求出常数项的值．‎ ‎【解答】解：（﹣）n的展开式中只有第四项的二项式系数最大所以n=6．‎ ‎ 其通项公式Tr+1=C6r•（﹣1）r•x，‎ 令﹣6=0，求得r=4，可得展开式中的常数项为C64•（﹣1）4=15，‎ 故答案为：15．‎ ‎　‎ ‎14．在直角坐标系xOy中，设集合Ω={（x，y）|0≤x≤2，0≤y≤1}，在区域Ω内任取一点P（x，y），则满足x+y≥1的概率是　　．‎ ‎【考点】几何概型．‎ ‎【分析】画出满足条件的平面区域，求出阴影部分的面积，从而求出满足条件的概率即可．‎ ‎【解答】解：画出满足条件的平面区域，如图示：‎ ‎，‎ 四边形OABC的面积是2，‎ 四边形ABCD的面积是2﹣=，‎ 故P==，‎ 故答案为：．‎ ‎　‎ ‎15．一个圆经过椭圆=1的三个顶点．且圆心在x轴的正半轴上．则该圆标准方程为　（x﹣）2+y2=　．‎ ‎【考点】椭圆的标准方程．‎ ‎【分析】利用椭圆的方程求出顶点坐标，然后求出圆心坐标，求出半径即可得到圆的方程．‎ ‎【解答】解：一个圆经过椭圆=1的三个顶点．且圆心在x轴的正半轴上．‎ 可知椭圆的右顶点坐标（4，0），上下顶点坐标（0，±2），‎ 设圆的圆心（a，0），则，解得a=，‎ 圆的半径为：，‎ 所求圆的方程为：（x﹣）2+y2=．‎ 故答案为：（x﹣）2+y2=．‎ ‎　‎ ‎16．已知命题p：“函数在R上有零点”，命题q：函数f（x）=在区间（1，+∞）内是减函数，若p∧q为真命题，则实数m的取值范围为　[，1]　．‎ ‎【考点】复合命题的真假．‎ ‎【分析】分别求出p，q为真时的m的范围，根据若p∧q为真命题，取交集即可．‎ ‎【解答】解：函数在R上有零点，‎ 即﹣=m2﹣+有解，‎ 令g（x）=﹣≤﹣，‎ 故m2﹣+≤﹣，‎ 解得：≤m≤2；‎ 故p为真时：m∈[，2]；‎ 函数f（x）=在区间（1，+∞）内是减函数，‎ 则m≤1，‎ 若p∧q为真命题，则p真q真，‎ 故，‎ 故答案为：[，1]．‎ ‎　‎ 三、解答题（本大题共6小题，共70分，要求写出必要的文字说明、证明过程和演算步骤）‎ ‎17．已知a为实数，p：点M（1，1）在圆（x+a）2+（y﹣a）2=4的内部； q：∀x∈R，都有x2+ax+1≥0．‎ ‎（1）若p为真命题，求a的取值范围；‎ ‎（2）若q为假命题，求a的取值范围；‎ ‎（3）若“p且q”为假命题，且“p或q”为真命题，求a的取值范围．‎ ‎【考点】复合命题的真假；复合命题．‎ ‎【分析】对于命题p为真，要利用点与圆的位置关系；对于命题q为真，要利用一元二次函数图象的特点，最后利用复合命题真假解决．‎ ‎【解答】解：（1）∵p：点M（1，1）在圆（x+a）2+（y﹣a）2=4的内部 ‎∴（1+a）2+（1﹣a）2＜4，解得﹣1＜a＜1，‎ 故p为真命题时a的取值范围为（﹣1，1）． ‎ ‎（2）∵q：∀x∈R，都有x2+ax+1≥0‎ ‎∴若q为真命题，则△=a2﹣4≤0，解得﹣2≤a≤2，‎ 故q为假命题时a的取值范围（﹣∞，﹣2）∪（2，+∞）． ‎ ‎（3）∵“p且q”为假命题，且“p或q”为真命题 ‎∴p与q一真一假，从而 ‎①当p真q假时有，无解；‎ ‎②当p假q真时有，解得﹣2≤a≤﹣1或1≤a≤2． ‎ ‎∴实数a的取值范围是[﹣2，﹣1]∪[1，2]．‎ ‎　‎ ‎18．已知椭圆，动直线 ‎（1）若动直线l与椭圆C相交，求实数m的取值范围；‎ ‎（2）当动直线l与椭圆C相交时，证明：这些直线被椭圆截得的线段的中点都在直线3x+2y=0上．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】（1）联立直线方程与椭圆方程，由判别式大于0求得实数m的取值范围；‎ ‎（2）由（1）中的方程结合根与系数的关系可得直线l被椭圆所截线段中点的坐标，代入直线3x+2y=0成立，说明直线被椭圆截得的线段的中点都在直线3x+2y=0上．‎ ‎【解答】（1）解：将代入，整理得：9x2+6mx+2m2﹣18=0，‎ 由△=36m2﹣36（2m2﹣18）=﹣36m2+36×18＞0，‎ 解得，‎ ‎∴实数m的取值范围是（）；‎ ‎（2）证明：设直线l与椭圆C相交于A（x1，y1），B（x2，y2），由（1）知，‎ ‎∴，‎ 故线段AB的中点，‎ 代入直线3x+2y=0，可得3×．‎ ‎∴直线被椭圆截得的线段的中点都在直线3x+2y=0上．‎ ‎　‎ ‎19．4月23人是“世界读书日”，某中学在此期间开展了一系列的读书教育活动，为了解本校学生课外阅读情况，学校随机抽取了100名学生对其课外阅读时间进行调查，下面是根据调查结果绘制的学生日均课外阅读时间（单位：分钟）的频率分布直方图，若将日均课外阅读时间不低于60分钟的学生称为“读书谜”，低于60分钟的学生称为“非读书谜”‎ ‎（1）根据已知条件完成下面2×2的列联表，并据此判断是否有99%的把握认为“读书谜”与性别有关？‎ 非读书迷 读书迷 合计 男 ‎15‎ 女 ‎45‎ 合计 ‎（2）将频率视为概率，现在从该校大量学生中，用随机抽样的方法每次抽取1人，共抽取3次，记被抽取的3人中的“读书谜”的人数为X，若每次抽取的结果是相互独立的，求X的分布列，期望E（X）和方程D（X）‎ 附：K2=n=a+b+c+d P（K2≥k0）‎ ‎0.100‎ ‎0.050‎ ‎0.025‎ ‎0.010‎ ‎0.001‎ k0‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎10.828‎ ‎【考点】离散型随机变量的期望与方差；独立性检验．‎ ‎【分析】（1）利用频率分布直方图，直接计算填写表格，然后利用个数求解K2，判断即可．‎ ‎（2）求出概率的分布列，然后利用超几何分布求解期望与方差即可．‎ ‎【解答】解：（1）完成下面的2×2列联表如下 非读书迷 读书迷 合计 男 ‎40‎ ‎15‎ ‎55‎ 女 ‎20‎ ‎25‎ ‎45‎ 合计 ‎60‎ ‎40‎ ‎100‎ ‎…‎ ‎≈8.249‎ VB8.249＞6.635，故有99%的把握认为“读书迷”与性别有关…‎ ‎（2）视频率为概率．则从该校学生中任意抽取1名学生恰为读书迷的概率为．由题意可知X～B（3，），P（x=i）= （i=0，1，2，3）…‎ 从而分布列为 X ‎0‎ ‎1‎ ‎2‎ ‎3‎ P ‎．…‎ E（x）=np=，D（x）=np（1﹣p）= …‎ ‎　‎ ‎20．在奥运会射箭决赛中，参赛号码为1～4号的4名射箭运动员参加射箭比赛．‎ ‎（1）通过抽签将他们安排到1～4号靶位，试求恰有2名运动员所抽靶位号与其参赛号码相同的概率；‎ ‎（2）记1号、2号射箭运动员射箭的环数为ξ（ξ所有取值为0，1，2，3，…，10）分别为P1，P2．根据教练员提供的资料，其概率分布如下表：‎ ξ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ P1‎ ‎0‎ ‎0‎ ‎0‎ ‎0‎ ‎0.06‎ ‎0.04‎ ‎0.06‎ ‎0.3‎ ‎0.2‎ ‎0.3‎ ‎0.04‎ P2‎ ‎0‎ ‎0‎ ‎0‎ ‎0‎ ‎0.04‎ ‎0.05‎ ‎0.05‎ ‎0.2‎ ‎0.32‎ ‎0.32‎ ‎0.02‎ ‎①若1，2号运动员各射箭一次，求两人中至少有一人命中9环的概率；‎ ‎②判断1号、2号射箭运动员谁射箭的水平高？并说明理由．‎ ‎【考点】离散型随机变量的期望与方差；离散型随机变量及其分布列．‎ ‎【分析】（1）本题是一个等可能事件的概率，试验发生包含的事件是把4名运动员安排到4个位置，从4名运动员中任取2名，其靶位号与参赛号相同，有C42种方法，另2名运动员靶位号与参赛号均不相同的方法有1种，得到概率．‎ ‎（2）①‎ 至少有一人命中9环的对立事件是两人各射击一次，都未击中9环，先做出都未击中9环的概率，用对立事件的概率公式得到结果，②根据所给的数据做出两个人的击中环数的期望，比较两个期望值的大小，得到结论2号射箭运动员的射箭水平高．‎ ‎【解答】解：（1）由题意知本题是一个等可能事件的概率，试验发生包含的事件是把4名运动员安排到4个位置，‎ 从4名运动员中任取2名，其靶位号与参赛号相同，有C42种方法，‎ 另2名运动员靶位号与参赛号均不相同的方法有1种，‎ ‎∴恰有2名运动员所抽靶位号与参赛号相同的概率为P==0.25‎ ‎（2）①由表可知，两人各射击一次，都未击中9环的概率为 P=（1﹣0.3）（1﹣0.32）=0.476‎ ‎∴至少有一人命中9环的概率为p=1﹣0.476=0.524‎ ‎②∵Eξ1=4×0.06+5×0.04+6×0.06+7×0.3+8×0.2+9×0.3+10×0.04=7.6‎ Eξ2=4×0.04+5×0.05+6×0.05+7×0.2+8×0.32+9×0.32+10×0.02=7.75‎ 所以2号射箭运动员的射箭水平高．‎ ‎　‎ ‎21．已知曲线x2+y=8与x轴交于A，B两点，动点P与A，B连线的斜率之积为．‎ ‎（1）求动点P的轨迹C的方程．‎ ‎（2）MN是动点P轨迹C的一条弦，且直线OM，ON的斜率之积为．求的最小值．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】（1）由已知曲线方程求出A，B的坐标，设P（x，y），结合kAPkBP=列式求得动点P的轨迹C的方程；‎ ‎（2）设直线MN的方程为y=kx+m，M（x1，y1），N（x2，y2），联立直线方程与椭圆方程，由根与系数的关系结合直线OM，ON的斜率之积为可得m与k的关系，进一步求出的范围得答案．‎ ‎【解答】解：（1）在方程x2+y=8中令y=0得：x=±2，‎ ‎∴A（﹣2，0），B（2，0）．‎ 设P（x，y），则kAPkBP=，整理得：，‎ 动点P的轨迹C的方程为；‎ ‎（2）设直线MN的方程为y=kx+m，M（x1，y1），N（x2，y2），‎ 联立，得（1+2k2）x2+4kmx+2m2﹣8=0，‎ ‎∴x1+x2=﹣，x1x2=，‎ y1y2=（kx1+m）（kx2+m）=k2•+km•+m2=，‎ ‎∵kOMkON=﹣，∴，即，‎ 得m2=4k2+2，‎ ‎∴=x1x2+y1y2=，‎ ‎∴﹣2≤＜2，‎ 故的最小值为﹣2．‎ ‎　‎ ‎22．已知椭圆C：的离心率，且过点Q ‎（1）求椭圆C的方程．‎ ‎（2）椭圆C长轴两端点分别为A，B，点P为椭圆上异于A，B的动点，定直线x=4与直线PA，PB分别交于M，N两点，直线PA，PB的斜率分别为k1，k2‎ ‎①证明；‎ ‎②若E（7，0），过E，M，N三点的圆是否过x轴上不同于点E的定点？若经过，求出定点坐标；若不经过，请说明理由．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】（1）由题意可知：e==，即a=2c，b2=a2﹣c2=3c2，将Q代入椭圆方程，即可求得c的值，则求得a和b的值，即可求得椭圆C的方程；‎ ‎（2）①由（1）得A（﹣2，0），B（2，0），设P（x，y），由直线的斜率公式可知：则，②令PA：y=k1（x+2），则M（4，6k1），同理求得N（4，2k2），kEM=﹣=﹣2k1，kEN=﹣， •=﹣1，即可求得m=1，故过点E，M，N三点的圆是以MN为直径的圆，过x轴上不同于点E的定点F（1，0）．‎ ‎【解答】解：（1）椭圆C：焦点在x轴上，由e==，即a=2c，‎ 则b2=a2﹣c2=3c2，‎ 由椭圆过点Q，代入，解得：c=1，‎ ‎∴a=2，b=，‎ ‎∴椭圆的标准方程：；‎ ‎（2）①证明：由（1）得A（﹣2，0），B（2，0），设P（x，y），‎ 则，‎ ‎②设PA，PB的斜率分别为k1，k2，P（x0，y0），则k1k2=﹣，‎ 可令PA：y=k1（x+2），则M（4，6k1），‎ PB：y=k2（x﹣2），则N（4，2k2），‎ 又kEM=﹣=﹣2k1，kEN=﹣，‎ ‎∴kEMkEN=﹣1，‎ 设圆过定点F（m，0），则•=﹣1，解得m=1或m=7（舍），‎ 故过点E，M，N三点的圆是以MN为直径的圆，过x轴上不同于点E的定点F（1，0）．‎ ‎　‎ ‎2017年1月13日