2020届二轮复习规划学案(全国通用)
规划
规划问题是不等式部分的重要内容,主要包括平面区域的表示、线性规划问题、非线性规划问题、线性规划在实际生活中的应用等知识.
平面区域的表示
· 二元一次不等式表示的平面区域
已知直线 l:Ax+By+C=0,它把坐标平面分为两部分,每个部分叫做开半平面,开半平面与 l 的并集叫做闭半平面.以不等式解 x,y 为坐标的所有点构成的集合,叫做不等式表示的区域或不等式的图象.
对于直线 l:Ax+By+C=0 同一侧的所有点 x,y,代数式 Ax+By+C 的符号相同,所以只需在直线某一侧任取一点 x0,y0 代入 Ax+By+C,由 Ax0+By0+C 符号即可判断出 Ax0+By0+C>0 (或 <0)表示的是直线哪一侧的点集.直线 Ax+By+C=0 叫做这两个区域的边界(boundary).
· 二元一次不等式组表示的平面区域
二元一次不等式组所表示区域的确定方法:①直线定界;②由几个不等式组成的不等式组所表示的平面区域,是各个不等式所表示的平面区域的公共部分.
线性规划
· 线性规划的有关概念
若约束条件是关于变量的一次不等式(方程),则称为线性约束条件(objective function).
一般地,满足线性约束条件的解 x,y 叫做可行解(feasible solution),由所有可行解组成的集合叫做可行域(feasible region).
要求最大(小)值所涉及的关于变量 x,y 的一次解析式叫做线性目标函数(linear objectives).
使目标函数取得最大值或最小值的可行解叫做最优解.
在线性约束条件下,求线性目标函数的最大值或最小值问题叫做线性规划问题(linear program).
非线性规划
对于在线性约束条件下的非线性目标函数求解,常将目标函数变形,掌握其几何意义,应用数形结合思想将其目标函数转化为几何问题求解.
精选例题
规划
1. 若 x,y 满足 x-2y⩽0,x-y+2⩾0,x+2y-4⩽0, 则 z=x+y 的最大值为 .
【答案】 3
2. 设不等式组 x+y-2⩾0,x-3y+6⩾0,x-y⩽0 表示的平面区域为 D,若直线 kx-y+k=0 上存在区域 D 上的点,则 k 的取值范围是 .
【答案】 12,2
3. 已知整点 Pa,3 在不等式组 3x+5y-25⩽0,x-4y⩽0,x⩾1 表示的平面区域内,则 a 的值为 .
【答案】 1 或 2 或 3
【分析】 将 Pa,3 代人不等式组得 3a-10⩽0,a-12⩽0,a⩾1, 即 a⩽103,a⩽12,a⩾1. 所以 1⩽a⩽103,又 a 是整数,所以 a=1 或 a=2 或 a=3.
4. 已知实数 x,y 满足 x-2y+1⩾0,∣x∣-y-1⩽0. 则 z=2x+y 的最大值为 .
【答案】 8
【分析】 提示:目标函数 z=2x+y 在点 A3,2 处取得最大值,最大值为 8.
5. 已知实数 x,y 满足约束条件 x+y+5⩾0,x-y⩽0,y⩽0, 则 z=3x+4y 的最小值是 .
【答案】 -352
【分析】 作出满足约束条件的平面区域如图所示,则当目标函数 y=-34x+z4 过点 A-52,-52 时,z 取得最小值为 -352.
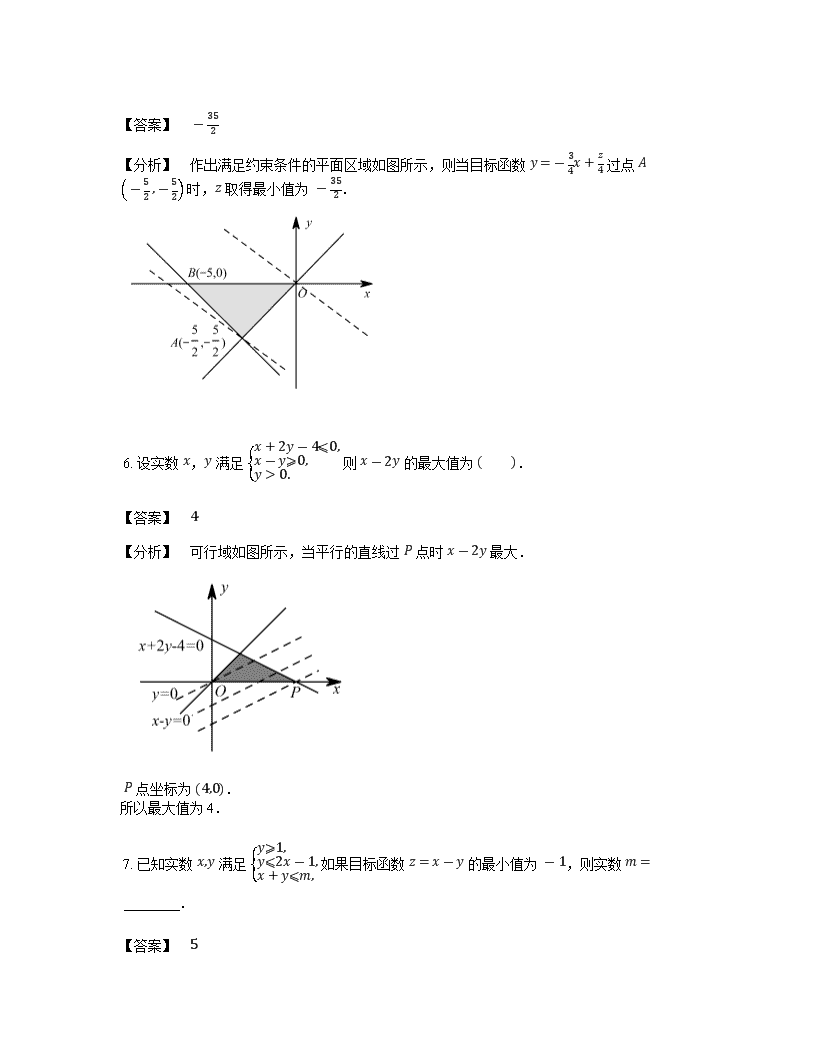
6. 设实数 x,y 满足 x+2y-4⩽0,x-y⩾0,y>0. 则 x-2y 的最大值为 .
【答案】 4
【分析】 可行域如图所示,当平行的直线过 P 点时 x-2y 最大.
P 点坐标为 4,0.
所以最大值为4.
7. 已知实数 x,y 满足 y⩾1,y⩽2x-1,x+y⩽m, 如果目标函数 z=x-y 的最小值为 -1,则实数 m= .
【答案】 5
8. 设 x,y 满足约束条件 x-y+2⩾02x+y-5⩽0y⩾2,则 z=3x+2y 的最大值为 .
【答案】 9
9. 已知实数 x,y 满足 x+y-5⩽0,2x-y+2⩾0,y⩾0, 则目标函数 z=x-y 的最小值为 .
【答案】 -3
10. 已知实数 x,y 满足约束条件 x⩾0,y⩾2x+1,x+y+k⩽0,(k 为常数),若目标函数 z=2x+y 的最大值是 113,则实数 k 的值是 .
【答案】 -3
【分析】 由题意得当 k<-1 时满足题意,此时该不等式组表示的平面区域如图所示,
平移直线 2x+y=0 经过点 P 时,目标函数 z=2x+y 取得最大值 113,
联立 2x-y+1=0,x+y+k=0, 得 x=-k+13,y=1-2k3,
即点 P-k+13,1-2k3,
所以 2×-k+13+1-2k3=113,
解得 k=-3.
11. 设 x,y 满足 x⩾0,y⩾0,3x+y⩽13,2x+3y⩽18.
(1)求 z=y+1x+1 的最小值;
【解】 画出不等式组表示的平面区域,如图阴影部分所示.
观察图象可知 zmin=0+1133+1=316.
(2)求 z=x+12+y+12 的最大值.
【解】 观察图象可知 zmax=0+12+6+12=50.
12. 如图,写出阴影区域(包含直线)所对应的二元—次不等式组.
【解】 可以由原点与直线的位置来确定它所在区域对应的二元一次方程.x⩾1,x-2y+3⩾0,x-y⩽0.
13. 已知 x,y 满足 x-y+2⩾0,x+y-4⩾0,2x-y-5⩽0.
(1)求 z=x2+y2+2x-2y+2 的最小值;
【解】 作出可行域,如下图所示.
因为 z=x+12+y-122,
所以 z 可看作是可行域内任一点 x,y 到点 M-1,1 的距离的平方.
有图可知 zmin 等于点 M 到直线 x+y-4=0 的距离的平方.
所以 zmin=-422=8.
(2)求 z=x+2y-4 的最大值.
【解】 因为 z=x+2y-4=5⋅x+2y-45,
所以 z 可看作是可行域内任一点 x,y 到直线 x+2y-4=0 的距离的 5 倍.
由图可知,点 C 到直线 x+2y-4=0 的距离大.
由 x-y+2=0,2x-y-5=0, 得点 C7,9.
所以 zmax=7+2×9-45×5=21.
14. 某纺纱厂生产甲,乙两种棉纱,已知生产甲种棉纱 1 吨需耗一级子棉 2 吨,二级子棉 1 吨;生产乙种棉纱需耗一级子棉 1 吨,二级子棉 2 吨,每 1 吨甲种棉纱的利润是 600 元,每 1 吨乙种棉纱的利润是 900 元,工厂在生产这两种棉纱的计划中要求消耗一级子棉不超过 300 吨,二级子棉不超过 250 吨.甲,乙两种棉纱应各生产多少(精确到吨),能使利润总额最大?
【解】 将已知数据列成下表:
设生产甲,乙两种棉纱分别为 x 吨,y 吨,利润总额为 z 元,
那么 2x+y⩽300x+2y⩽250x⩾0y⩾0
z=600x+900y.
作出以上不等式组所表示的平面区域(如图),即可行域.
做直线 l:600x+900y=0,即直线 l:2x+3y=0,把直线 l 向右上方平移至 l1 的位置时,直线经过可行域上的点 M,且与原点距离最大,此时 z=600x+900y 取最大值.解方程组
2x+y=300x+2y=250
的 M 的坐标为 x=3503≈117,y=2003≈67.
答:应生产甲种棉纱 117 吨,乙种棉纱 67 吨,能使利润总额达到最大.
15. 设点 Px,y 满足:x+y-3⩽0,x-y+1⩾0,x⩾1,y⩾1.,求 yx+xy 的取值范围.
【解】 设 k=yx=y-0x-0.
则 yx+xy=k+1k,
又因为
x+y-3⩽0,x-y+1⩾0,x⩾1,y⩾1..
所以分别在点 1,2,2,1 处 k 取得最大最小值.
所以 k∈12,2
所以 yx+xy=k+1k⩾2,(当且仅当 x=1 时等号成立)
所以 k+1k 的最大值为 52
所以 yx+xy 的取值范围为 2,52
16. 某企业生产甲乙两种产品,已知生产每吨甲产品要用 A 原料 3 吨,B 原料 2 吨;生产每吨乙产品要用 A 原料 1 吨,B 原料 3 吨,销售每吨甲产品可获得利润 5 万元,销售每吨乙产品可获得利润 3 万元.该企业在一个生产周期消耗 A 原料不超过 13 吨,B 原料不超过 18 吨.问该企业如何安排可获得最大利润,最大利润是多少?
【解】 设生产甲产品 x 吨,生产乙产品 y 吨,则有关系:
A原料B原料甲产品x吨3x2x乙产品y吨y3y
则 x>0,y>0,3x+y⩽13,2x+3y⩽18.
目标函数 z=5x+3y.
作出可行域(如图),
平移直线 5x+3y=0,过点 B 时 z 取最大值.
由 3x+y=13,2x+3y=18.⇒x=3,y=4. 即 B3,4,
所以当 x=3,y=4 时,Zmax=5×3+3×4=27,
故生产甲产品 3 吨,生产乙产品 4 吨时,可获得最大利润为 27 万元.
17. 某厂使用 A,B 两种零件装配甲、乙两种产品,该厂的生产能力是月产甲最多 2500 件,月产乙最多 1200 件,而组装一件甲需要 4 个 A 、 2 个 B;组装一件乙需要 6 个 A 、 8 个 B.某月,该厂能用的 A 最多有 14000 个,B 最多有 12000 个.用不等式将甲、乙两种产品产量之间的关系表示出来.
【解】 设甲、乙两种产品产量分别为 x,y 件,则
0⩽x⩽2500,0⩽y⩽1200,4x+6y⩽14000,2x+8y⩽12000,x,y∈N*,
即 0⩽x⩽2500,0⩽y⩽1200,2x+3y⩽7000,x+4y⩽6000,x,y∈N*.
18. 已知向量 a=x,2,b=1,y,其中 x,y⩾0.若 a⋅b⩽4,求 y-x 的取值范围.
【解】 由已知可得 x+2y⩽4,x⩾0,y⩾0,
由线性规划知识可知点 x,y 在不等式组约束下表示的是坐标轴与直线 x+2y=4 所围成的三角形区域,观察图可知 y-x 在点 0,2 处取得最大值 2,在点 4,0 处取得最小值 -4.
所以 y-x 的取值范围是 -4,2.
19. 已知变量 x,y 满足 x-y⩽1,2x+y⩽5,x⩾1.
(1)画出不等式组表示的平面区域;
【解】 不等式组表示平面区域如阴影部分所示.
(2)设 z=3x+y,求 z 的最大值及相应点的坐标.
【解】 因为 z=3x+y 即因为 y=-3x+z,
z 为直线的纵截距.
如图作直线 y=-3x,平移该直线,当平移到经过该阴影部分的 P 点时,纵截距 z 最大.
x-y=1,2x+y=5. 解得点 P2,1,
此时 z=3x+y 取得最大值是 7.
20. 2013 年国内部分省市遭受雾霾天气,严重影响着人们的生活,某科技公司拟投资开发新型节能环保产品,策划部制定投资计划时,不仅要考虑可能获得的盈利,而且还要考虑可能出现的亏损.经过市场调查公司打算投资甲、乙两个项目,根据预测,甲、乙项目可能的最大盈利率分别为 100% 和 60%,可能的最大亏损率分别为 20% 和 10%.投资人计划投资金额不超过 100 万元,要求确保可能的资金亏损不超过 16 万元.问投资公司对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
【解】 设投资人分别用 x 万元、 y 万元投资甲、乙两个项目,
由题意,得 x+y⩽100,0.2x+0.1y⩽16,x⩾0,y⩾0, 目标函数 z=x+0.6y.
上述不等式组表示的可行域为如图所示的阴影部分(含边
界).
作直线 l0:x+0.6y=0,并作平行于 l0 的一组直线 x+0.6y=z,z∈R,与可行域相交.
当直线经过可行域上的 A 点时,z 取得最大值.
由方程组 x+y=100,0.2x+0.1y=16, 解得 x=60,y=40,
此时 z=60+0.6×40=84,
所以当 x=60,y=40 时,投资公司可能盈利最大.
答:投资人用 60 万元投资甲项目、 40 万元投资乙项目,才能确保亏损不超过 16 万元的前提下,使可能的盈利最大.
平面区域的表示
1. 在直角坐标平面上,不等式组 y⩾12x,y⩽-∣x∣+3, 所表示的区域的面积为 .
【答案】 12
2. 已知不等式组 x⩽0,y⩾0,y-x⩽4 表示平面区域 M,若 -4⩽a⩽t 时,动直线 x+y=a 所经过的平面区域 M 的面积为 7,则 t= .
【答案】 2
【分析】 作出可行域(如图阴影部分),
当 a⩽0 时,动直线 x+y=a 扫过的平面区域是三角形,
此时的面积 S⩽12×22×22=4,
故要使平面区域 M 的面积为 7,动直线应在如图所示的位置,
此时设动直线交 y 轴于点 C,且 BC=m,
从而 7=12×4×4-12×m2×m2,
解得 m=2,故 t=4-m=2.
3. 在平面直角坐标系 xOy 中,M 为不等式组 2x+3y-6⩽0x+y-2⩾0y⩾0 所表示的区域上一动点,则 ∣OM∣ 的最小值为 .
【答案】 2
4. 若直线 y=2x 上存在点 x,y 满足约束条件 x+y-3⩽0,x-2y-3⩽0,x⩾m, 则实数 m 的取值范围为 .
【答案】 -∞,1
5. 点 -2,t 在直线 2x-3y+6=0 的上方,则 t 的取值范围是 .
【答案】 t>23
6. 在平面直角坐标系中,不等式组 x+y-2⩾0,x-y+2⩾0,x⩽2 表示的平面区域的面积是 .
【答案】 4
【分析】 不等式组 x+y-2⩾0,x-y+2⩾0,x⩽2 表示的平面区域如图所示,其平面区域的面积 S=12×4×2=4.
7. 已知直线 l:x+y+1=0,点 Aa,1,B2,a 在直线 l 的同侧,则 a 的取值范围是 .
【答案】 -∞,-3∪-2,+∞
【分析】 ∵ 直线 l 同侧的点使 x+y+1 的值的符号相同,
∴a+1+12+a+1>0,即 a+2a+3>0,
∴a<-3 或 a>-2.
8. 实数 x,y 满足 y⩾∣x-2∣,1⩽y⩽3, 则不等式组所表示的平面区域的面积为 .
【答案】 8
【分析】 作出其平面区域图如下:
可知是上底长 2,下底长 6,高为 2 的梯形,则阴影部分的面积为 12×2+6×2=8.
9. 不等式组 x⩾0x+3y⩾43x+y⩽4 所表示的平面区域的面积等于 .
【答案】 43
【分析】 做出不等式组所表示的平面区域,如图中阴影部分所示,即 △ABC,S△ABC=12×4-43×1=43.
10. 若点 1,1 在直线 x-2y+b=0 的左上方,则实数 b 的取值范围是 .
【答案】 b<1
11. 已知点 P-1,2 及其关于原点的对称点均在不等式 2x-ky+1>0 表示的平面区域内,求实数 k 的取值范围.
【解】 点 P 的坐标代入不等式,得 2×-1-k⋅2+1>0,解得 k<-12;
点 P 关于原点的对称点的坐标代入不等式,得 2×1-k⋅-2+1>0,k>-32.
故实数 k 的取值范围为 -32
0,x+2y+1⩾0,10,且 a≠1)的图象过区域 M 的实数 a 的取值范围.
【解】 2,9
根据不等式组,画出平面区域如图所示,当函数 y=ax(a>0,且 a≠1)的图象过区域时,点 A1,9,B3,8 为两个边界点,根据对数函数的性质,求解出 a=9 和 a=2,所以 2⩽a⩽9.
19. 已知区域 D 是以点 A4,1,B-1,-6,C-3,2 为顶点的三角形区域(包括边界与内部),如图所示.
(1)写出表示区域 D 的不等式组;
【解】 用两点式求得直线 AB,AC,BC 的方程分别为:
yx-5y-23=0,x+7y-11=0,4x+y+10=0,
因为原点 0,0 在区域 D 内,
所以表示区域 D 的不等式组为 7x-5y-23⩽0,x+7y-11⩽0,4x+y+10⩾0.
(2)设点 B,C 分别在直线 4x-3y-a=0 的异侧,求 a 的取值范围.
【解】 将 B 的坐标代入 4x-3y-a,得 14-a.
将 C 的坐标代入 4x-3y-a,得 -18-a.
根据题意,得 14-a-18-a<0.
解得 -181,变量 x,y 在约束条件 y⩾x,y⩽mx,x+y⩽1. 下,目标函数 z=x+my 的最大值为 2,则 m= .
【答案】 1+2
【分析】 作出可行域如图所示,当直线 z=x+my 经过点 B 时,z 有最大值,
此时点 B 的坐标为 1m+1,mm+1,z=1m+1+m⋅mm+1=2,
解之得 m=1+2 或 m=1-2(舍去),所以 m=1+2.
5. 已知变量 x,y 满足约束条件 x+y⩾2,x-y⩽1,y⩽2, 则目标函数 z=-2x+y 的取值范围是 .
【答案】 -4,2
6. 已知实数 x,y 满足 3x+2y⩽7y-x⩽1x⩾0y⩾0,则 u=3x+4y 的最大值是 .
【答案】 11
7. 变量 x,y 满足线性约束条件 3x+y-2⩽0,y-x⩽2,y⩾-x-1. 目标函数 z=kx-y 仅在点 0,2 取得最小值,则 k 的取值范围是 .
【答案】 -30,b>0 的最大值为 35,则 a+b 的最小值为 .
【答案】 8
【分析】 满足约束条件的平面区域如图阴影部分,当直线 y=-abx+z 过点 2,3 时,z 有最大值 35,即 2ab+3=35,则 ab=16,所以 a+b⩾2ab=8,当且仅当 a=b 时取等号.
9. 设变量 x,y 满足约束条件 2x+y-2⩾0,x-2y+4⩾0,x-1⩽0 则目标函数 z=3x-2y 的最小值为 .
【答案】 -2
10. 已知实数 x,y 满足条件 x-y⩾0,x+y⩾0,x⩽1, 则 y-12x 的最大值为 .
【答案】 12
【分析】 作出约束条件所表示的平面区域(如图中阴影部分所示),
令 t=y-12x,即 y=12x+t,当目标函数经过点 A1,1 时,取得最大值,最大值为 1-12=12.
11. 某营养师要为某个儿童预定午餐和晚餐.已知一个单位的午餐含 12 个单位的碳水化合物,6 个单位的蛋白质和 6 个单位的维生素 C;一个单位的晚餐含 8 个单位的碳水化合物,6 个单位的蛋白质和 10 个单位的维生素 C.另外,该儿童这两餐需要的营养中至少含 64 个单位的碳水化合物,42 个单位的蛋白质和 54 个单位的维生素 C.如果一个单位的午餐、晚餐的费用分别是 2.5 元和 4 元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
【解】 设为该儿童分别预订 x、y 个单位的午餐和晚餐,共花费 z 元,则 z=2.5x+4y,
且满足以下条件
12x+8y⩾64,6x+6y⩾42,6x+10y⩾54,x,y⩾0,
化简得
3x+2y⩾16,x+y⩾7,3x+5y⩾27,x,y⩾0,
作出可行域如图,则 z 在可行域的四个顶点 A9,0,B4,3,C2,5,D0,8 处的值分别为
zA=2.5×9+4×0=22.5,zB=2.5×4+4×3=22,zC=2.5×2+4×5=25,zD=2.5×0+4×8=32.
比较之,zB 最小,因此应当为该儿童预定 4 个单位的午餐和 3 个单位的晚餐,就可以满足要求.
12. 一名农民有田 2 亩,根据他的经验,若种水稻,则每亩每期产量为 400 千克;若种花生,则每亩每期产量为 100 千克,但水稻成本较高,每亩每期需 240 元,而花生只需要 80 元,且花生每千克可卖 5 元,稻米每千克可卖 3 元,现在他只能凑足 400 元,问这位农民对两种作物各种多少亩,才能得到最大利润?
【解】 设种水稻 x 亩,花生 y 亩,利润为 z 元,由题意可得下表:
亩数产量kg/亩售价元/kg成本元/亩水稻x4003240花生y100580
∴ 利润 z=400x⋅3-240x+500y-80y=960x+420y=6016x+7y.
∴x,y 满足 x+y⩽2,240x+80y⩽400,x⩾0,y⩾0, 即 x+y⩽2,3x+y⩽5,x⩾0,y⩾0.
作出 x,y 所满足的线性约束条件的可行域,如图.
A 点的坐标为方程组 x+y=2,3x+y=5 的解,∴A32,12.
要求 16x+7y=t 的最大值,由图知,当动直线过点 A32,12 时,t 有最大值,即 z 有最大值.
∴zmax=60×16×32+7×12=1650(元).
答:这位农民种 1.5 亩水稻,0.5 亩花生时才能得到最大利润 1650 元.
13. 已知 O 为坐标原点,A2,1,Px,y 满足 x-4y+3⩽0,3x+5y⩽25,x-1⩾0, 求 OPcos∠AOP 的最大值.
【解】 OPcos∠AOP=OPOA⋅cos∠AOPOA=OA⋅OPOA=2x+y5.
令 N=2x+y,则本题转化为求 N=2x+y 在约束条件
x-4y+3⩽0,3x+5y⩽25,x-1⩾0 下的最大值.
画出可行或如图:
由图可知当直线 N=2x+y 经过点 A 时,N 有最大值.
由 x-4y+3=0,3x+5y-25=0 得 x=5,y=2.
所以 Nmax=12,
所以 OPcos∠AOP 的最大值为 1255.
14. 制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目,根据预测,甲、乙两个项目可能的最大盈利率分别为 100% 和 50%,可能的最大亏损率分别为 30% 和 10%,投资人计划投资金额不超过 10 万元,要求确保可能的资金亏损不超过 1.8 万元,则投资人对甲、乙两个项目各投资多少万元才能使可能的盈利最大?
【解】 设投资人分别用 x,y 万元投资甲,乙两个项目,盈利 z 万元,则目标函数为 z=x+0.5y.
由题意,得
x+y⩽10,0.3x+0.1y⩽1.8,x⩾0,y⩾0,
上述不等式组表示的平面区域如图所示,阴影部分(含边界)即为可行域.
作直线 l0:x+0.5y=0,并作平行于直线 l0 的一组直线 x+0.5y=z,z∈R,与可行域相交,其中有一条直线经过可行域上的点 M,此时 z 最大,这里点 M 是直线 x+y=10 与直线 0.3x+0.1y=1.8 的交点.
解方程组
x+y=10,0.3x+0.1y=1.8.
得
x=4,y=6,
此时,z=4+0.5×6=7(万元).
所以当 x=4,y=6 时,z 取得最大值 7 万元.
答:投资人用 4 万元投资甲项目,6 万元投资乙项目,才能使可能的盈利最大.
15. 某工艺品加工厂准备生产具有收藏价值的奥运会标志—“中国印·舞动的北京”和奥运会吉祥物—“福娃”.该厂所用的主要原料为 A 、 B 两种贵金属,已知生产一套奥运会标志需用原料 A 和原料 B 的量分别为 4 盒和 3 盒,生产一套奥运会吉祥物需用原料 A 和原料 B 的量分别为 5 盒和 10 盒.若奥运会标志每套可获利 700 元,奥运会吉祥物每套可获利 1200 元,该厂月初一次性购进原料 A 、 B 的量分别为 200 盒和 300 盒.问该厂生产奥运会标志和奥运会吉祥物各多少套才能使该厂月利润最大?最大利润为多少?
【解】 设该厂每月生产奥运会标志和奥运会吉祥物分别为 x,y 套,月利润为 z 元,
由题意得 4x+5y⩽200,3x+10y⩽300,x⩾0,y⩾0,
目标函数为 z=700x+1200y.
作出二元一次不等式组所表示的平面区域,即可行域,如图所示:
目标函数可变形为 y=-712x+z1200,
-45<-712<-310,
∴ 当 y=-712x+z1200 通过图中的点 A 时,z1200 最大,z 最大.
解 4x+5y=200,3x+10y=300 得点 A 坐标为 20,24.
将点 A20,24 代入 z=700x+1200y 得 zmax=700×20+1200×24=42800(元).
答:该厂生产奥运会标志和奥运会吉祥物分别为 20 、 24 套时月利润最大,最大利润为 42800 元.
16. 某企业生产甲、乙两种产品,已知生产每吨甲产品要用 A 原料 3 吨,B 原料 2 吨;生产每吨乙产品要用 A 原料 1 吨,B 原料 3 吨,销售每吨甲产品可获得利润 5 万元,销售每吨乙产品可获得利润 3 万元.该企业在一个生产周期内消耗 A 原料不超过 13 吨,B 原料不超过 18 吨.求该企业获得的最大利润.
【解】 设生产甲产品 x 吨,生产乙产品 y 吨,则有关系
A 原料B 原料甲产品 x 吨3x2x乙产品 y 吨y3y
则有
x>0,y>0,3x+y⩽13,2x+3y⩽18.
目标函数 z=5x+3y.
作出可行域后求出可行域边界上各端点的坐标,
经验证知:当 x=3,y=4 时可获得最大利润为 27 万元.
17. 已知变量 x 、 y 满足约束条件 x+2y-3⩽0,x+3y-3⩾0,y-1⩽0. 若目标函数 z=ax+y(其中 a>0)仅在点 3,0 处取得最大值,试求 a 的取值范围.
【解】 由题意作出可行域,如图所示:
解出 A3,0 、 B1,1 、 C0,1,要使 z=ax+y 在点 3,0 处取得最大值,必须有 -a12.∴a 的取值范围是 12,+∞.
18. 电视台为某广告公司特约播放两套片集,其中片集甲每片播映时间为 20 分钟,广告时间为 1 分钟,收视观众为 60 万;片集乙每片播映时间为 10 分钟,广告时间为 1 分钟,收视观众为 20 万.广告公司规定每周至少有 6 分钟广告,而电视台每周只能为该公司提供不多于 86 分钟的节目时间(含广告时间).问电视台每周应播映两套片集各多少集,才能获得最高的收视率?
【解】 设片集甲播映 x 集,片集乙播映 y 集,则有
x+y⩾6,21x+11y⩽86,x⩾0,y⩾0,x,y∈N.
要使收视率最高,则只要 z=60x+20y 最大即可.如图所示,作出可行域,
易知满足题意的最优解为 2,4,
所以 zmax=60×2+20×4=200,故电视台每周片集甲播映 2 集,片集乙播映 4 集,其收视率最高.
19. 一辆货车的最大载重量为 30 吨,要装载 A 、 B 两种不同的货物,已知装载 A 货物每吨收入 40 元,装载 B 货物每吨收入 30 元,且要求装载的 B 货物不少于 A 货物的一半.请问 A 、 B 两种不同的货物分别装载多少吨时,载货得到的收入最大?并求出这个最大值.
【解】 设装载 A 货物 x 吨,装载 B 货物 y 吨,收入 z 元,则 z=40x+30y,x,y 满足约束条件 x+y⩽30y⩾12xx≥0y≥0,做出不等式所表示的平面区域如图所示:
则目标函数在点 A20,10 取得最大值,zmax=1100,此时装载 A 货物 20 吨,B 货物 10 吨.
20. 本地一公司计划 2011 年在省、市两个电视台做总时间不超过 300 分钟的广告,广告总费用不超过 9 万元,省、市电视台的广告收费标准分别为 500 元 / 分钟和 200 元 / 分钟,规定省、市两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为 0.3 万元和 0.2 万元.问该公司如何分配在省、市两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
【解】 设公司在省电视台和市电视台做广告的时间分别为 x 分钟和 y 分钟,总收益为 z 元,由题意得
x+y⩽300,500x+200y⩽90000,x⩾0,y⩾0.
目标函数为
z=3000x+2000y.
二元一次不等式组等价于
x+y⩽300,5x+2y⩽900,x⩾0,y⩾0.
如图,作出二元一次不等式组所表示的平面区域,即可行域.
作直线 l:3000x+2000y=0,即 3x+2y=0,平移直线 l.
从图中可知,当直线 l 过 M 点时,目标函数取得最大值.
联立方程组
x+y=300,5x+2y=900.
解得 x=100,y=200,即点 M 的坐标为 100,200.
从而 zmax=3000x+2000y=700000.
因此,在省电视台和市电视台做广告的时间分别为 100 分钟和 200 分钟时,总收益最大为 70 万元.
非线性规划
1. 设定点 A3,0,动点 Px,y 的坐标满足约束条件 x⩾2,y⩾2,x+y⩽6, 则 ∣OP∣cos∠AOP(O 为坐标原点)的最大值为 .
【答案】 4
【分析】 依题意,得 ∣OP∣cos∠AOP=OP⋅OA∣OA∣=3x+03=x.
作出动点 Px,y 的坐标满足约束条件的可行域(如图),
由图可知,当点 P 是直线 x+y=6 与 y=2 的交点时,x 取得最大值.
由 x+y=6,y=2, 解得 P4,2.
所以 x 的最大值为 4,即 ∣OP∣cos∠AOP 的最大值为 4.
2. 已知变量 x,y 满足条件 x⩾0,y⩽-x+3,y⩾2x 则 yx-2 的取值范围是 .
【答案】 -2,0
【分析】 作出 x,y 在线性约束条件下的可行域(如图所示),
yx-2 的几何意义是表示连接 2,0 和平面区域内的点 x,y 的直线的斜率,
显然当直线过点 O0,0 时斜率取最大值 0,当直线过点 A1,2 时斜率取最小值 -2,
故 yx-2 的取值范围是 -2,0.
3. 已知实数 x,y 满足约束条件 x+y⩾3,y⩽3,x⩽3, 则 z=5-x2-y2 的最大值为 .
【答案】 12
【分析】 在坐标系中画出约束条件所对应的可行域如下图:
又 x2+y2 的几何意义为如图所示的阴影区域中任一点 P 到原点距离的平方,
所以由几何特征可得 x2+y2 的最小值为原点到直线 AC 的距离的平方.
故 z=5-x2-y2⩽5-|3|22=5-92=12,
即 zmax=12.
解法 2 由基本不等式 x2+y2⩾2xy 可得 2x2+y2⩾x+y2.
又 x+y⩾3,故 x2+y2⩾92,当且仅当 x=y=32⩽3 时取得,
所以 zmax=5-92=12.
4. 如果直线 2ax-by+14=0a>0,b>0 和函数 fx=mx+1+1m>0,m≠1 的图象恒过同一个定点,且该定点始终落在圆 x-a+12+y+b-22=25 的内部或圆上,那么 ba 的取值范围为 .
【答案】 34,43
【分析】 函数 fx=mx+1+1 恒过定点 -1,2.
代入直线方程得:a+b=7,
点在圆内或者圆上得:a2+b2⩽25,
设 Pa,b,如图所示:
线段 AB 上的点满足条件,ba 可看做直线 OP 的斜率,最大为 kOB,最小为 kOA.
联立解得:A4,3,B3,4,
所以 ba 的取值范围为 34,43.
5. 已知 x,y 满足条件 x+y+2>0x+2y+1⩽0y⩾0,则 r=x-12+y-22 的值域是 .
【答案】 8,17
【分析】 画出可行域,要求的 r 即为可行域内的点到点 M1,2 间的距离的平方.
6. 若变量 x 和 y 满足条件 x+y-3⩾0x-2y⩾0,则 z=2x+y 的最小值为 ;yx 的取值范围是 .
【答案】 5;-1,12
7. 已知点 Aa,b 与点 B1,0 在直线 3x-4y+10=0 的两侧,给出下列说法:
① 3a-4b+10>0;
② 当 a>0 时,a+b 有最小值,无最大值;
③ a2+b2>2;
④ 当 a>0 且 a≠1,b>0 时,ba-1 的取值范围为 -∞,-52∪34,+∞.
其中,所有正确说法的序号是 .
【答案】 ③④
【分析】 根据题意,得 3a-4b+103×1-4×0+10<0,即 3a-4b+10<0,于是,在坐标系 aOb 中,点 Aa,b 在直线 3a-4b+10=0 上方的平面区域内运动.
因为平面区域是不封闭的,所以 a+b 既无最大值,也无最小值;原点到直线 3a-4b+10=0 的距离为 2,所以 a2+b2>2 成立;
由于 a>0,a≠1,b>0,所以平面区域是在直线 3a-4b+10=0 上方、纵轴右侧的平面区域内(不包括直线 a=1 上的点).而 ba-1 表示点 a,b 与点 1,0 连线的斜率 k,由图形知,k<-52 或 k>34.
8. 在平面直角坐标系 xOy 中,点 Px,y 是椭圆 x23+y2=1 的一个动点,则 Z=x+y 的最大值为 .
【答案】 2
【分析】
如图,当直线 y=-x+Z 与椭圆相切的时候,直线截距 Z 取得最大值 2.
9. 设集合 M=x,y∣x⩾0x+3y⩾43x+y⩽4,则集合 z∣z=34x+y,x,y∈M 中元素的最小值是 .
【答案】 43
10. 设 x 、 y 满足约束条件 x+y⩾1,x-2y⩾-2,3x-2y⩽3, 若 z=x2+4y2,则 z 的取值范围是 .
【答案】 45,532
【分析】 z=x2+4y2 表示中心在坐标原点、焦点在 x 轴上的椭圆,当椭圆与直线 x+y=1 相切时,z=x2+4y2 最小.
由 z=x2+4y2,x+y=1, 得 5y2-2y+1-z=0.由 Δ=0,得 z=45,即 z 的最小值为 45.
当椭圆过点 A52,94 时,z 的最大值 为 532.
11. 设变量 x,y 满足 x-4y+3⩽0,3x+5y-25⩽0,x⩾1.
(1)设 z=yx,求 z 的最小值;
【解】 由约束条件 x-4y+3⩽03x+5y-25⩽0x⩾1 作出 x,y 的可行域如图所示.
由 x=13x+5y-25=0 解得 A1,225.
由 x=1,x-4y+3=0 解得 C1,1.
由 x-4y+3=03x+5y-25=0 解得 B5,2.
z=yx=y-0x-0 表示的几何意义是可行域中的点与原点 O 连线的斜率.
结合图形可知 zmin=kOB=25.
(2)设 z=x2+y2,求 z 的取值范围.
【解】 z=x2+y2 的几何意义是可行域上的点到原点 O 的距离的平方.
结合图形可知,可行域上的点到原点的距离中,dmin=∣OC∣=2,dmax=∣OB∣=29.
∴z 的取值范围为 2,29.
12. 已知实数 x 、 y 满足 2x+y-2⩾0,x-2y+4⩾0,3x-y-3⩽0, 试求 z=y+1x+1 的最大值和最小值.
【解】 由于 z=y+1x+1=y--1x--1,所以 z 的几何意义是点 x,y 与点 M-1,-1 连线的斜率,因此 y+1x+1 的最值就是点 x,y 与点 M-1,-1 连线的斜率的最值.
结合图可知:直线 MB 的斜率最大,直线 MC 的斜率最小,即 zmax=kMB=3,此时 x=0,y=2;zmin=kMC=12,x=1,y=0.
13. 已知实数 x,y 满足 x+y-1⩽0,x-y+1⩾0,y⩾-1, 且 u=x2+y2-4x-8y+20,求 u 的最小值.
【解】 u=x2+y2-4x-8y+20=x-22+y-42,即求可行域内的点 x,y 到点 P2,4 的距离的平方的最小值.作可行域如图
可见 umin=PA2,x-y+1=0x+y-1=0,⇒A0,1,
∴umin=2-02+4-12=13.
14. 已知实数 x,y 满足 x2+y2-2x-2y+1⩾0,1⩽x⩽2,1⩽y⩽2.
(1)mx-y+1⩾0 恒成立,求实数 m 的最大值;
【解】 作出不等式所表示的平面区域如图中阴影部分所示,直线 y=mx+1 恒过定点 0,1,则使 mx-y+1⩾0 恒成立,则直线经过 AC 时直线的斜率最大,所以实数 m 的最大值为 1.
1.
(2)求 xx2+y2 的取值范围.
【解】 不等式组所表示的平面区域如图中阴影部分所示,连接 OA,OB,则 yx∈12,2,所以 xx2+y2=11+yx2∈55,255.
15. 设 x,y 满足约束条件 1⩽x⩽3,-1⩽x-y⩽0.
(1)求 z=2x-y 的最大值.
【解】 作出可行域如图阴影部分.
作直线 2x-y=0,并向右平移,当平移至直线过点 B 时,z=2x-y 取最大值.
而由得 B3,3.所以 zmax=2×3-3=3.
(2)若 z=x2+y2,求 z 的取值范围.
【解】 z=x2+y2 表示可行域内的点到原点的距离,观察可行域知,可行域内的点 A 和点 C 到原点的距离分别为最大和最小.
又由 x=1,x-y=0, 得 A1,1.
由 x=3,x-y=-1, 得 C3,4.
故 ∣OA∣=1+1=2,∣OC∣=32+42=5.
所以 z 的取值范围为 2,5.
16. 已知 x-y+2⩾0,x+y-4⩾0,2x-y-5⩽0, 求:
(1) z=x+2y-4 的最大值;
【解】 作出可行域如图所示,并求出顶点的坐标 A1,3,B3,1,C7,9.
平移直线 x+2y-4=z,当其经过点 C 时,z 取最大值,将 C7,9 代入 得 z 的最大值为 21.
(2) z=x2+y2-10y+25 的最小值;
【解】 z=x2+y-52 表示可行域内任一点 x,y 到定点 M0,5 的距离的平方,过 M 作直线 AC 的垂线,易知垂足 N 在线段 AC 上,故 z 的最小值是 MN2=92.
(3) z=2y+1x+1 的范围.
【解】 z=2⋅y--12x--1 表示可行域内任一点 x,y 与定点 Q-1,-12 连线的斜率的两倍.
∵kQA=74,kQB=38,
∴z 的范围为 34,72.
17. 设 fx=x2-6x+5,若实数 x,y 满足条件 fy⩽fx⩽0,求 yx 的最大值和最小值.
【解】 由题意知 y2-6y+5⩽x2-6x+5⩽0,所以 y2-x2-6y+6x⩽0,x2-6x+5⩽0, 即 y-xy+x-6⩽0,1⩽x⩽5 .
不等式组表示的区域如图所示.
设 k=yx,即当点 Px,y 在区域内运动时,求从原点出发的直线的斜率的最大值和最小值,
当 P 与 A1,5 重合时,kmax=5,
当 P 与 C5,1 重合时,kmin=15.
所以 yx 的最大值为 5,最小值为 15.
18. 已知 x-y+2⩾0,x+y-4⩾0,2x-y-5⩽0. 求:
(1) z=x2+y2-10y+25 的最小值;
【解】 z=x2+y-52 表示可行域内任一点 x,y 到点 M0,5 的距离的平方,如图,过 M 作 AC 的垂线,易知垂足 N 在线段 AC 上.故
MN=0-5+21+-12=32=322,
MN2=3222=92,
所以 z 的最小值为 92.
(2) z=2y+1x+1 的范围.
【解】 z=2⋅y--12x--1 表示可行域内点 x,y 与定点 Q-1,-12 连线斜率的 2 倍.如图,因为
kQA=74, kQB=38,
所以 z 的范围是 34,72.
19. 已知 x,y 满足 x-4y⩽-3,3x+5y⩽25,x⩾1, 求 z=yx-3 的取值范围.
【解】 作出可行域,如图.
设 Mx,y,N3,0,则 z=yx-3=kMN,其中点 M 在 △ABC 所包含的区域内(含边界).
易求得 kNA=2-05-3=1,kAB=1-01-3=-12,所以 z⩾1 或 z⩽-12.
20. 已知实数 x,y 满足不等式组 y⩾0,x-y⩾0,2x-y-2⩾0, 求 z=y-1x+1 的取值范围.
【解】 依题意画图如下.
因为目标函数 z=y-1x+1 对应的几何意义是点 P-1,1 与区域里面的点的连线的斜率,
所以当直线过点 A1,0 时,斜率取到最小值 -12,
当直线平行于直线 y=x 时斜率为 1,故直线斜率的取值范围是 -12,1,
即 z=y-1x+1 的取值范围是 -12,1.
课后练习
1. 设 x,y 满足约束条件 x⩾0x-2y⩾0x-y⩽1,则 z=2x-y 的最大值是 .
2. 设实数 x,y 满足条件 x⩾0,x⩽y,x+2y⩽3. 则 z=2x-y 的最大值是 .
3. 设实数 x,y 满足约束条件 3x-y-6⩽0,x-y+2⩾0,x⩾0,y⩾0, 则 z=2x+3y 的最大值是 .
4. 动直线 l:3λ+1x+1-λy+6-6λ=0 过定点 P,则点 P 的坐标为 ,若直线 l 与不等式组 x⩾0,y⩾0,2x+y⩽2 表示的平面区域有公共点,则实数 λ 的取值范围是 .
5. 若不等式 x-y+5⩾0,y⩾a,0⩽x⩽2, 表示的平面区域是一个三角形,则 a 的取值范围 .
6. 关于 x,y 的不等式组 2x-3y+7⩾01⩽x⩽4y⩾1 所构成的区域面积为 .
7. 已知实数 x,y 满足 2x+y⩾1,则 u=x2+y2+4x-2y 的最小值为 .
8. 不等式组 y⩽x2x-3y⩽0x+y⩽10x-3y-a⩽0 表示的平面区域是三角形,则实数 a 的取值范围是 .
9. 能表示图中阴影部分的二元一次不等式组是 .
10. 原点和点 1,1 在直线 x+y-a=0 的两侧,则 a 的取值范围是 .
11. 如实数 x,y 满足约束条件 2x-y⩽2,x-y⩾-12x+y⩽4, 则目标函数 z=2x+y 的最小值为 .
12. 已知 x,y 满足约束条件 x+y-2⩽0,x-2y-2⩽0,2x-y+2⩾0. 若 z=y-ax 取得最大值的最优解不唯一,则实数 a 的值为 .
13. 在直角坐标系中,△ABC 的三个顶点坐标分别为 A0,2,B-1,0,C1,0,动点 Px,y 是 △ABC 内的点(包括边界).若目标函数 z=ax+by 的最大值为 2,且此时的最优解所确定的点 Px,y 是线段 AC 上的所有点,则目标函数 z=ax+by 的最小值为 .
14. 设 x,y 满足约束条件 x+y-7⩽0,x-3y+1⩽0,3x-y-5⩾0, 则 z=2x-y 的最大值为 .
15. 设 x,y 满足约束条件 x-y⩾-1,x+y⩽3,x⩾0,y⩾0, 则 z=x-2y 的取值范围为 .
16. 已知区域 D:y⩾2,x+y-2⩾0,x-y-1⩽0, 则 x2+y2 的最小值是 ;若圆 C:x-a2+y-22=2 与区域 D 有公共点,则实数 a 的取值范围是 .
17. 已知实数 x,y 满足 y⩾12x-1,y⩽-23|x|+1, 则 z=14x2+y 的最大值为 .
18. 如果实数 x,y 满足关系 x-y+1⩾0,x+y-2⩽0,x⩾0,y⩾0. 则 z=2x+y-7x-3 的取值范围为 .
19. 满足约束条件 ∣x∣+2∣y∣⩽2 的目标函数 z=y-x 的最小值是 .
20. 已知实数 x,y 满足 y⩽1,x⩽1,x+y⩾1, 则 z=x2+y2 的最小值为 .
21. 设 O 为坐标原点,A1,1,若点 Bx,y 满足 x2+y2-2x-2y+1⩾0,1⩽x⩽2,1⩽y⩽2, 试求 OA⋅OB 的最大值.
22. 在坐标平面上画出不等式组 y⩾∣x-1∣,y⩽-∣x∣+3, 所表示的平面区域并求出其面积.
23. 某家具厂生产甲、乙两种型号的桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张甲、乙型的桌子分别需要 1 小时和 2 小时,漆工油漆一张甲、乙型的桌子分别需要 3 小时和 1 小时.又木工、漆工每天工作分别不得超过 8 小时和 9 小时.请列出满足生产条件的数学关系式,并画出相应的平面区域.
24. 画出不等式组 x<3,2y⩾x,3x+2y⩾6 表示的平面区域.
25. 若不等式组 x⩾0,x+3y⩾4,3x+y⩽4. 所表示的平面区域被直线 y=kx+43 分为面积相等的两部分,求 k 的值.
26. 如图所示,写出阴影区域(包含直线)所对应的二元一次不等式组.
27. 已知点 Pa2-a,1 在不等式 x+y<3 表示的平面区域内,但不在不等式 2x+3y<3 表示的平面区域内,求实数 a 的取值范围.
28. 某工厂制造A型电子装置 45 台,B型电子装置 55 台,需要薄钢板为每台装置配一外壳.已知薄钢板的面积有两种规格:甲种每张面积为 2 m2,可做A,B两型电子装置外壳分别 3 个和 5 个;乙种每张面积 3 m2,可做A,B两型电子装置外壳各 6 个,请用平面区域表示甲乙两种薄钢板张数的取值范围.
29. 不等式组 2x+y-2⩾0,x-2y+4⩾0,3x-y-3⩽0. 表示的平面区域记为 C.
(1)画出平面区域 C,并求出 C 包含的整点(即横、纵坐标均为整数的点)的个数;
(2)求平面区域 C 的面积.
30. 已知点 Mt,1 在不等式组 x-2y+3>0,x+4y+8>0,3x+y-4<0 所表示的平面区域内,试求整数 t.
31. 若 x+1-y2y-1-x2=0,求 x-y 的最大、最小值.
32. 某运输公司有 12 名驾驶员和 19 名工人,有 8 辆载重量为 10 吨的甲型卡车和 7 辆载重量为 6 吨的乙型卡车.某天需送往 A 地至少 72 吨的货物,派用的每辆车需满载且只能送一次.派用的每辆甲型卡车需配 2 名工人,运送一次可得利润 450 元;派用的每辆乙型卡车需配 1 名工人,运送一次可得利润 350 元,问该公司如何合理计划当天派用两类卡车的车辆数,可得最大利润?并求出最大利润.
33. 要购买单价为 25 元的篮球和单价为 15 元的排球若干个,总金额不超过 150 元,且每种球至少要购买 2 个.
(1)共有多少种购买方法?
(2)若要正好用完 150 元,应如何购买?
34. 某家具厂有方木料 90 m3,五合板 600 m2,准备加工成书桌和书橱.已知生产每张书桌需要方木料 0.1 m3,五合板 2 m2;生产每个书橱需要方木料 0.2 m3,五合板 1 m2.家具厂生产书桌 x 张,书橱 y 个,请从中提炼出一个关于 x,y 的不等式组.
35. 已知平面区域 D 由以 P1,2,Q-3,4,R3,5 为顶点的三角形内部和边界组成.
(1)写出表示区域 D 的不等式组.
(2)设点 x,y 在区域 D 内变动,求目标函数 z=2x+y 的最小值.
(3)若在区域 D 内有无穷多个点 x,y 可使目标函数 z=mx+y m<0 取得最小值,求实数 m 的值.
36. 已知 x-y+2⩾0x+y-4⩾02x-y-5⩽0,求 z=x2+y2-10y+25 的最小值.
37. 已知实数 x,y 满足不等式组 x+y-1⩽0,x-y+1⩾0,y⩾-1. 求 x2+y2-4x-4y+8 的最小值.
38. 不等式组 x-y+5⩾0,x+y⩾0,x⩽3 表示的平面区域是什么形状?若 u=x+22+y+12,求在上述约束条件下 u 的最小值.
(1)求 z=2x+y 的最大值,使 x,y 满足约束条件 y⩽x,x+y⩽1,y⩾-1.
(2)求 z=2x+y 的最大值,使 x,y 满足约束条件 x225+y216=1.
40. 在平面直角坐标系中,点 Px,y 满足约束条件:7x-5y-23⩽0x+7y-11⩽04x+y+10⩾0.
(1)在给定的坐标系中画出满足约束条件的可行域(用阴影表示,并注明边界的交点);
(2)设 u=y+7x+4,求 u 的取值范围;
(3)已知两点 M2,1,O0,0,求 OM⋅OP 的最大值.
规划-出门考
姓名 成绩
1. 若实数 x,y 满足 12⩽x⩽1,y⩾-x+1,y⩽x+1. 则 y+1x 的取值范围是 .
2. 已知 x,y 满足约束条件 x⩽y⩽3x0⩽x⩽1x,y∈N,则目标函数 z=2x+y 的最大值为 .
3. 若 x,y 满足 x+y-2⩾0,kx-y+2⩾0,y⩾0. 且 z=y-x 的最小值为 -4,则 k 的值为 .
4. 已知 0loga3y-x+2,且 λ0表示的平面区域内的点是 .
9. 已知关于 x,y 的不等式组 0⩽x⩽2x+y-2⩾0kx-y+2⩾0 所表示的平面区域的面积为 3,则实数 k 的值为 .
10. 若 x+2xn 的展开式中各项的系数之和为 81,且常数项为 a,则直线 y=a6x 与曲线 y=x2 所围成的封闭区域面积为 .
11. 若变量 x,y 满足约束条件 x-2y⩽0,x-y+1⩾0,x+2y⩽2, 则目标函数 z=x+y 的最小值为 .
12. 在 △ABC 中,A2,4,B-1,2,C1,0,若 Qx,y 在 △ABC 内部和边界上运动,那么函数 z=x-y 的最大值为 .
13. 已知实数 x,y 满足 2x-y+4⩾0,x-y+3⩾0,x⩽0,y⩾0, 则目标函数 z=3y-2x 的最大值为 .
14. 若 x,y 满足 x-y⩾0,x+y⩽2,y⩾0, 则目标函数 f=x+2y 的最大值为 .
15. 设 m>1,在约束条件 y⩾xy⩽mxx+y⩽1 下,目标函数 z=x+5y 的最大值为 4,则 m 的值为 .
16. 在平面直角坐标系 xOy 中,若动点 Pa,b 到两直线 l1:y=x 和 l2:y=-x+2 的距离之和为 22,则 a2+b2 的最大值为 .
17. 设实数 x,y 满足 x⩽3,x-y+2⩾0,x+y-4⩾0. 则 x2+y2 的取值范围是 .
18. 如果点 P 在平面区域 x-1⩽0x+y-1⩾0y-2⩽0 上,点 Q 在曲线 x+22+y2=1 上,那么 PQ 的最大值为 .
19. 已知实数 x,y 满足 2x-y⩽0,x+y-5⩾0,y-4⩽0,,若不等式 ax2+y2⩾x+y2 恒成立,则实数 a 的最小值是 .
20. 已知变量 x,y 满足约束条件 x-y+2⩾0x+y-4⩾02x-y-5⩽0,则目标函数 z=x2+y2-10y+25 的最小值为 .
21. 已知甲、乙、丙三种食物的维生素 A 、 B 含量及成本如下表:
甲乙丙维生素A单位/ kg600700400维生素B单位/ kg800400500成本元/ kg1194
若用甲、乙、丙三种食物各 x kg 、 y kg 、 z kg 配成 100x kg 的混合食物,并使混合食物内至少含有 56000 单位维生素 A 和 63000 单位维生素 B.试用 x 、 y 表示混合食物成本 c 元,并写出 x 、 y 所满足的不等关系.
22. 某运输公司接受了向抗洪救灾地区每天送至少 180 t 支援物资的任务.该公司有 8 辆载重 6 t 的 A 型卡车与 4 辆载重为 10 t 的 B 型卡车,有 10 名驾驶员,每辆卡车每天往返的次数为 A 型卡车 4 次,B 型卡车 3 次;每辆卡车每天往返的成本费 A 型为 320 元,B 型为 504 元.请为公司安排一下,应如何调配车辆,才能使公司所花的成本费最低?若只安排 A 型或 B 型卡车,所花的成本费分别是多少?
23. 已知 一元二次方程 x2+ax+b=0 的一个根在 -2,-1 内,另一个根在 1,2 内,试用图表示出以 a,b 为坐标轴的点 a,b 的存在范围,并求出 a+b 的取值范围.
24. 设 x,y 满足 2x+y⩾4,x-y⩾1,x-2y⩽2.
(1)求 z=x+y 的最小值.
(2)求 z=2x-y 的最小值.
25. 已知甲、乙两煤矿每年的产量分别为 200 万吨和 300 万吨,需经过东车站和西车站两个车站运往外地.东车站每年最多能运 280 万吨煤,西车站每年最多能运 360 万吨煤,甲煤矿运往东车站和西车站的运费价格分别为 1 元/ 吨和 1.5 元/ 吨,乙煤矿运往东车站和西车站的运费价格分别为 0.8 元/ 吨和 1.6 元/ 吨.煤矿应怎样编制调运方案,能使总运费最少?
26. 画出不等式组 x-y+5⩾0,x+y⩾0,x⩽3 表示的平面区域,并回答下列问题:
(1)指出 x,y 的取值范围.
(2)平面区域内有多少个整点?
27. 在平面直角坐标系中,画出不等式组 y⩾x-1,y⩽-x+3 所表示的平面区域,并求出其面积.
28. 某工厂有甲、乙两种产品,计划每天各自的产量不少于 15 t,已知生产甲产品 1 t 需煤 9 t,电力 4 kW⋅h,劳力 3 个;生产乙产品 1 t 需煤 4 t,电力 5 kW⋅h,劳力 10 个.甲产品每吨利润 7 万元,乙产品每吨利润 12 万元,但每天用煤不超过 300 t,电力不超过 200 kW⋅h,劳力只有 300 个.列出满足生产条件的数学关系式,并画出相应的平面区域.
29. 若平面区域 x+y⩽2,kx+1⩾y+2, 是一个三角形,求实数 k 的取值范围.
30. 下表给出了 X,Y,Z 三种食物的维生素含量.
维生素A单位/kg维生素B单位/kgX300700Y500100Z300300
某人欲将这三种食物混合成 100 kg 的食品,要使混合食品中至少含 35000 单位的维生素 A 及 40000 单位的维生素 B,设 X,Y 这两种食物各取 x kg,y kg,那么 x,y 应满足怎样的关系?
31. 设 z=2y-2x+4,式中 x,y 满足 0⩽x⩽1,0⩽y⩽2,2y-x⩾1, 求 z 的最大值和最小值.
32. 设 x,y,z 满足约束条件 x+y+z=1,3y+z⩾2,0⩽x⩽1,0⩽y⩽1. 求 u=2x+6y+4z 的最大值和最小值.
33. 某单位在会议厅装备中,预算用 6000 元购买茶几和沙发,已知茶几和沙发的单价分别为 200 元和 300 元,希望使茶几和沙发的总数尽可能的多,但沙发数不少于茶几数的 2 倍且不多于茶几数的 3 倍,问茶几和沙发各买多少才行?
34. 浙江卫视为《中国好声音》栏目播放两套宣传片,其中宣传片甲播放时间为 3 分 30 秒,广告时间为 30 秒,收视观众为 60 万人,宣传片乙播放时间为 1 分钟,广告时间为 1 分钟,收视观众为 20 万人.广告公司规定每周至少有 4 分钟广告,而电视台每周只能为该栏目宣传片提供不多于 16 分钟的节目时间.两套宣传片每周至少各播一次,问电视台每周应播放两套宣传片各多少次,才能使得收视观众最多?
35. 若 x,y 满足约束条件 x+y⩾1x-y⩾-12x-y⩽2 且目标函数 z=ax+2y 仅在 1,0 处取得最小值,求 a 的取值范围.
36. 已知 x,y 满足条件 7x-5y-23⩽0,x+7y-11⩽0,4x+y+10⩾0. 求
(1) 4x-3y 的最大值和最小值;
(2) x2+y2 的最大值和最小值.
37. 已知实数 x,y 满足约束条件 2x+y-4⩾0,x-y+4⩾0,2x-y-2⩽0, 设目标函数 fx,y=x2+y2.求 fx,ymax,fx,ymin,并指出相应的 x,y 的值.