专题7-2+绝对值不等式（测）-2018年高考数学一轮复习讲练测（浙江版）

专题7-2+绝对值不等式（测）-2018年高考数学一轮复习讲练测（浙江版）

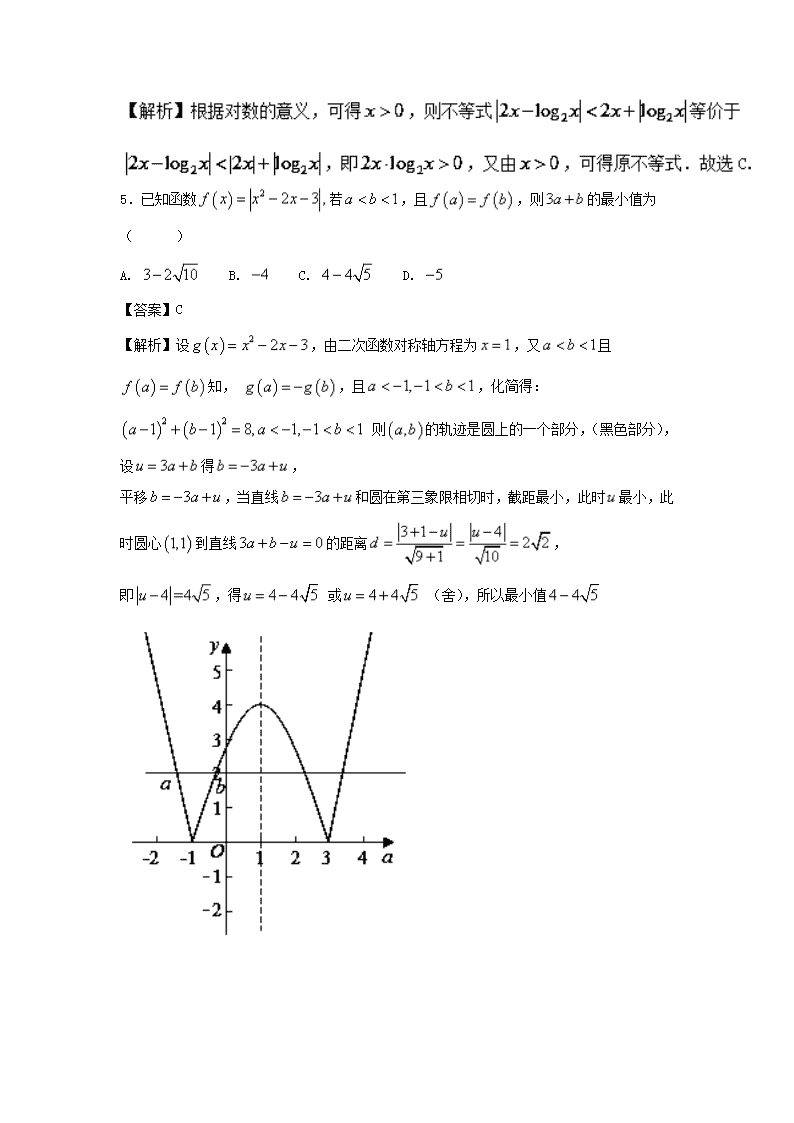
‎2018年高考数学讲练测【浙江版】【测】第七章 不等式与证明 第02节 绝对值不等式 班级__________ 姓名_____________ 学号___________ 得分__________‎ 一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选择中，只有一个是符合题目要求的.）‎ ‎1．【2017届浙江省高三上模拟】已知集合，，则（ ）‎ A. B. C. D.‎ ‎【答案】B.‎ ‎【解析】由题意得，，，∴，故选B.‎ ‎2.【2017届浙江温州二模】设集合，，则（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎3．【2017届浙江嘉兴高三上基础测试】已知，则“”是“”的（ ）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎【答案】B ‎【解析】设，如图涂色部分为，红色为，有是的真子集，故为必要不充分条件，选B．‎ ‎4.不等式成立，则( )‎ A. B. C. D. ‎ ‎【答案】C ‎5．已知函数若，且，则的最小值为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】设，由二次函数对称轴方程为，又且知， ，且，化简得： 则的轨迹是圆上的一个部分，（黑色部分），设得，‎ 平移，当直线和圆在第三象限相切时，截距最小，此时最小，此时圆心到直线的距离，‎ 即，得 或 （舍），所以最小值 ‎ ‎ ‎【点评】本题考查带绝对值的函数，作出函数f（x）结合已知求得，利用线性规划以及直线和圆相切的位置关系是解决本题的关键．渗透化归思想与数形结合思想，综合性较强，有一定的难度．‎ ‎6．【2018届山东、湖北部分重点中学高三第一次联考】已知函数的定义域为，不等式的解集为，则（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】因为，所以，由可得 ,所以，所以，故选B.‎ ‎7.【2017届天津滨海新区高三上八校联考】设集合， ， ，则的取值范围为（ ）‎ A. 或 B. C. D. 或 ‎【答案】B ‎8.如果，那么当时，代数式的最小值是（ ）‎ A. 30 B. 0 C. 15 D. 一个与有关的代数式 ‎【答案】C ‎【解析】∵，∴x−p⩾0，x−15⩽0，x−p−15⩽0，‎ ‎∴|x−p|+|x−15|+|x−p−15|=x−p+15−x+p+15−x=30−x，‎ 故当x=15时，|x−p|+|x−15|+|x−p−15|的最小值为30−15=15，‎ 故选：C.‎ ‎9．设 ， ， 是不为零的实数，那么 的值有（ ）‎ A. 3种 B. 4种 C. 5种 D. 6种 ‎【答案】B ‎【解析】当a，b，c>0时，x=1；‎ 当a，b，c三个数中两个大于0，一个小于0时，有c小于0或c大于0两种情况；‎ 有x=1+1+1=3，或x=0−1=-1‎ 当a，b，c三个数中两个小于0，一个大于0时，有c大于0或小于0两种情况，则x=−1-1-1=-3或x=0+1=1；‎ 当a，b，c<0时，x=−1.‎ 综上：x=-3，-1，1，3.‎ 故选B.‎ ‎10.如果关于的不等式，对于恒成立，则实数的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】由题意得,因为 ，所以 ，选C.‎ ‎11. 关于的不等式在上恒成立，则实数的取值范围为（ ）‎ A. B. C. D.‎ ‎【答案】D ‎12.若关于的不等式至少有一个负数解，则实数的取值范围是（ ）‎ A． B． ‎ C． D．‎ ‎【答案】D ‎【解析】关于的不等式，即，且，在同一坐标系中，画出和函数的图象，当函数的图象则左支经过点时，求得，当函数的图象则右支和图象相切时，方程组有唯一的解，即有唯一的解，故，解得，所以实数的取值范围是，故选D．‎ 二、填空题（本大题共4小题，每小题5分，共20分.把答案填在题中的横线上.）‎ ‎13. 不等式的解集是___________________．‎ ‎【答案】‎ ‎14．不等式的解集为________‎ ‎【答案】‎ ‎【解析】|2x-1|-|x-2|＜0 移向得：丨2x-1丨＜丨x-2丨 两边同时平方得（2x-1）2＜（x-2）2 即：4x2-4x+1＜x2-4x+4， 整理得：x2＜1，即-1＜x＜1 故答案为：{x|-1＜x＜1}．‎ ‎15.已知函数．若的解集包含，则实数的取值范围为__________．‎ ‎【答案】‎ ‎【解析】f(x)≤|x－4|⇔|x－4|－|x－2|≥|x＋a|.当x∈[1,2]时，|x－4|－|x－2|≥|x＋a|‎ ‎⇔4－x－(2－x)≥|x＋a|⇔－2－a≤x≤2－a.由条件得－2－a≤1且2－a≥2，‎ 即－3≤a≤0.故满足条件的a的取值范围为.‎ ‎16．存在使不等式成立，则的取值范围是_____‎ ‎【答案】‎ ‎【解析】由题意得 ‎.‎ 三、解答题 （本大题共4小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17．【2017届云南省红河州高三检测】设函数其中 当时，求不等式的解集；‎ 若不等式的解集为，求的值.‎ ‎【答案】(1) (2) ‎ 解析：（1）当时，不等式，即即，‎ 即 ，或．‎ 故原不等式的解集为． ‎ ‎（2）不等式即①，或②．‎ 解①可得 ，故①无解；‎ 解②可得， ‎ 故原不等式的解集为． ‎ 再根据已知原不等式的解集为，可得-， ‎ ‎18．【2017届广西高三5月模拟】已知函数.‎ ‎（1）解不等式；‎ ‎（2）若关于的不等式恒成立，求实数的取值范围.‎ ‎【答案】（1）（2）.‎ ‎【解析】【试题分析】（1）借助绝对值的定义分类直接求解可得；（2）运用等价转化的数学思想转化为求函数的最大值问题来求解：‎ 解：（1）可化为，‎ 即或或 解得或，所以不等式的解集为 .‎ ‎（2） 恒成立 ，‎ ‎ （当时取等号），‎ ‎；由，解得或，‎ 即的取值范围是 .‎ ‎19．已知函数. ‎ ‎(1) 若，求实数的取值范围;‎ ‎(2) 若R , 求证： .‎ ‎【答案】(Ⅰ ) ；(Ⅱ) 证明见解析.‎ 试题解析：(Ⅰ ) 因为，所以． ‎ ‎ ① 当时，得，解得，所以;‎ ‎ ② 当时，得，解得，所以;‎ ‎③ 当时，得，解得，所以; ‎ 综上所述，实数的取值范围是． ‎ ‎(Ⅱ) 因为R , ‎ ‎ 所以 ‎ ‎ ． ‎ ‎20.【2018届广雅中学、东华中学、河南名校高三上第一次联考】已知函数 .‎ ‎（1）若，解关于的不等式；‎ ‎（2）若，使，求的取值范围.‎ ‎【答案】（1），（2）.‎ 试题解析：（1）若，则不等式化为，‎ 若，则，解得，故；‎ 若，则，解得，故；‎ 若，则，解得，故无解，‎ 综上所述，关于的不等式的解集为，‎ ‎（2），使等价于，‎ 因为，‎ 所以，所以的最小值为，‎ 所以，得或 ‎ 所以的取值范围是.‎ ‎ ‎