高考数学人教A版（理）一轮复习：第二篇 第9讲 函数的应用

高考数学人教A版（理）一轮复习：第二篇 第9讲 函数的应用

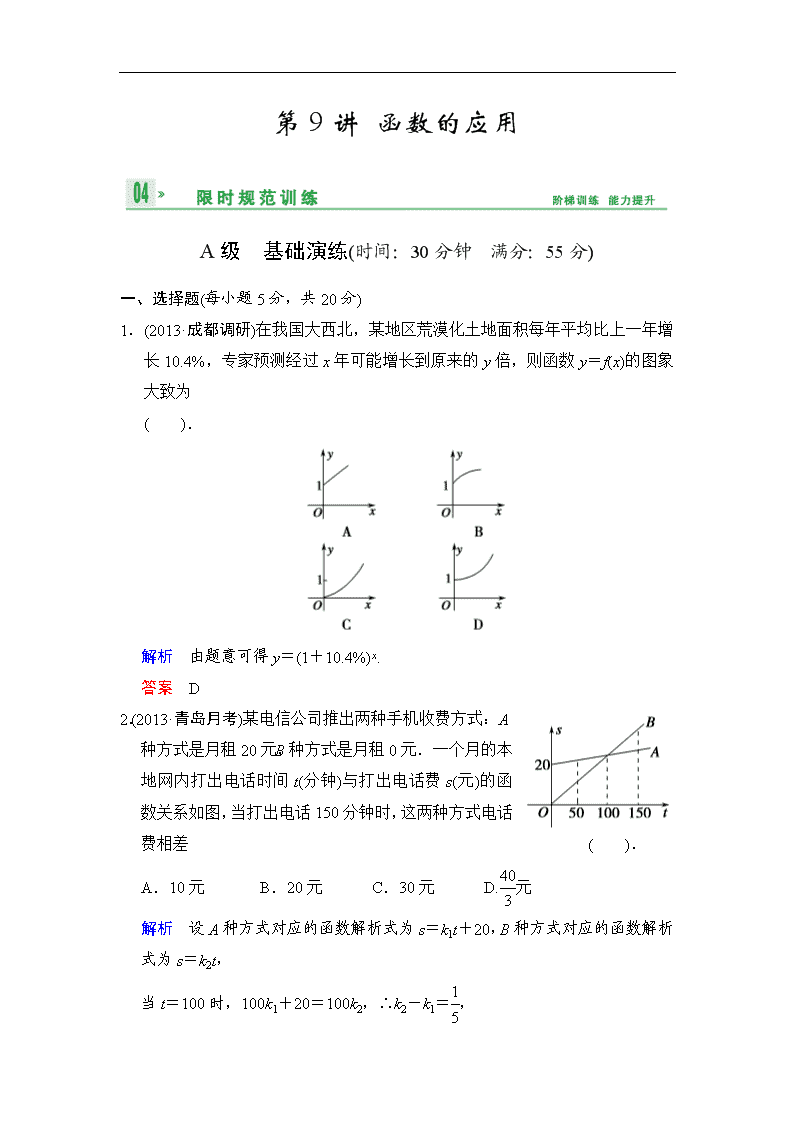
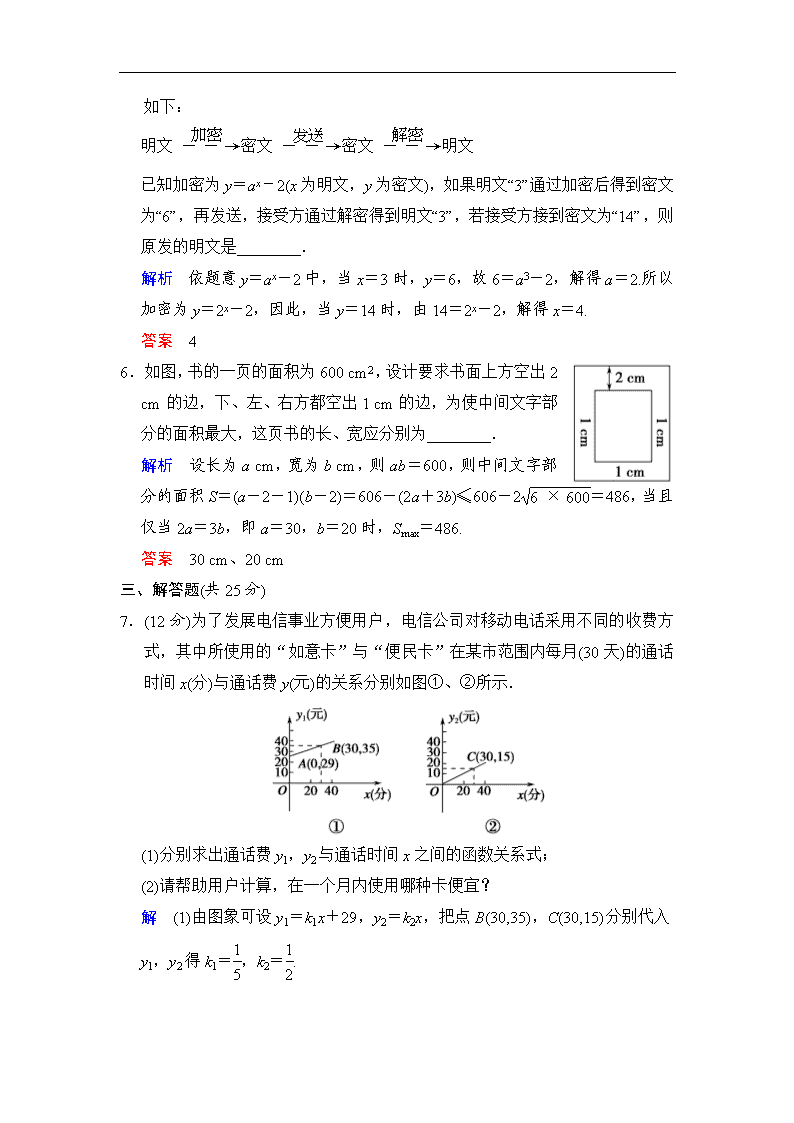
第9讲 函数的应用 A级　基础演练(时间：30分钟　满分：55分)‎ 一、选择题(每小题5分，共20分)‎ ‎1．(2013·成都调研)在我国大西北，某地区荒漠化土地面积每年平均比上一年增长10.4%，专家预测经过x年可能增长到原来的y倍，则函数y＝f(x)的图象大致为 (　　)．‎ 解析　由题意可得y＝(1＋10.4%)x.‎ 答案　D ‎2．(2013·青岛月考)某电信公司推出两种手机收费方式：A种方式是月租20元，B种方式是月租0元．一个月的本地网内打出电话时间t(分钟)与打出电话费s(元)的函数关系如图，当打出电话150分钟时，这两种方式电话费相差 (　　)．‎ A．10元 B．20元 C．30元 D.元 解析　设A种方式对应的函数解析式为s＝k1t＋20，B种方式对应的函数解析式为s＝k2t，‎ 当t＝100时，100k1＋20＝100k2，∴k2－k1＝，‎ t＝150时，150k2－150k1－20＝150×－20＝10.‎ 答案　A ‎3．某公司在甲、乙两地销售一种品牌车，利润(单位：万元)分别为L1＝5.06x－0.15x2和L2＝2x，其中x为销售量(单位：辆)．若该公司在这两地共销售15辆车，则能获得最大利润为 (　　)．‎ A．45.606万元 B．45.6万元 C．45.56万元 D．45.51万元 解析　依题意可设甲销售x辆，则乙销售(15－x)辆，总利润S＝L1＋L2，则总利润S＝5.06x－0.15x2＋2(15－x)＝－0.15x2＋3.06x＋30＝－0.15(x－10.2)2＋0.15×10.22＋30(x≥0)，∴当x＝10时，Smax＝45.6(万元)．‎ 答案　B ‎4．(2013·太原模拟)某汽车运输公司购买了一批豪华大客车投入营运，据市场分析每辆客车营运的总利润y(单位：10万元)与营运年数x(x∈N*)为二次函数关系(如图所示)，则每辆客车营运多少年时，其营运的年平均利润最大 (　　)．‎ A．3 B．4 C．5 D．6‎ 解析　由题图可得营运总利润y＝－(x－6)2＋11，则营运的年平均利润＝－x－＋12，‎ ‎∵x∈N*，∴≤－2 ＋12＝2，‎ 当且仅当x＝，即x＝5时取“＝”．‎ ‎∴x＝5时营运的年平均利润最大．‎ 答案　C 二、填空题(每小题5分，共10分)‎ ‎5．为了保证信息安全，传输必须使用加密方式，有一种方式其加密、解密原理如下：‎ 明文密文密文明文 已知加密为y＝ax－2(x为明文，y为密文)，如果明文“3”通过加密后得到密文为“6”，再发送，接受方通过解密得到明文“3”，若接受方接到密文为“14”，则原发的明文是________．‎ 解析　依题意y＝ax－2中，当x＝3时，y＝6，故6＝a3－2，解得a＝2.所以加密为y＝2x－2，因此，当y＝14时，由14＝2x－2，解得x＝4.‎ 答案　4‎ ‎6．如图，书的一页的面积为600 cm2，设计要求书面上方空出2 cm的边，下、左、右方都空出1 cm的边，为使中间文字部分的面积最大，这页书的长、宽应分别为________．‎ 解析　设长为a cm，宽为b cm，则ab＝600，则中间文字部分的面积S＝(a－2－1)(b－2)＝606－(2a＋3b)≤606－2＝486，当且仅当2a＝3b，即a＝30，b＝20时，Smax＝486.‎ 答案　30 cm、20 cm 三、解答题(共25分)‎ ‎7．(12分)为了发展电信事业方便用户，电信公司对移动电话采用不同的收费方式，其中所使用的“如意卡”与“便民卡”在某市范围内每月(30天)的通话时间x(分)与通话费y(元)的关系分别如图①、②所示．‎ ‎(1)分别求出通话费y1，y2与通话时间x之间的函数关系式；‎ ‎(2)请帮助用户计算，在一个月内使用哪种卡便宜？‎ 解　(1)由图象可设y1＝k1x＋29，y2＝k2x，把点B(30,35)，C(30,15)分别代入y1，y2得k1＝，k2＝.‎ ‎∴y1＝x＋29，y2＝x.‎ ‎(2)令y1＝y2，即x＋29＝x，则x＝96.‎ 当x＝96时，y1＝y2，两种卡收费一致；‎ 当x<96 时，y1>y2，即使用“便民卡”便宜；‎ 当x>96时，y10)，剩下的员工平均每人每年创造的利润可以提高0.2x%.‎ ‎(1)若要保证剩余员工创造的年总利润不低于原来1 000名员工创造的年总利润，则最多调整出多少名员工从事第三产业？‎ ‎(2)在(1)的条件下，若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润，则a的取值范围是多少？‎ 解　(1)由题意得：10(1 000－x)(1＋0.2x%)≥10×1 000，‎ 即x2－500x≤0，又x>0，所以00，所以00)，雨速沿E移动方向的分速度为c(c∈R)．E移动时单位时间内的淋雨量包括两部分：①P或P的平行面(只有一个面淋雨)的淋雨量，假设其值与|v－c|×S成正比，比例系数为；②其他面的淋雨量之和，其值为.记y为E移动过程中的总淋雨量．当移动距离d＝100，面积S＝时，‎ ‎(1)写出y的表达式；‎ ‎(2)设0

查看更多