高一数学（人教A版）必修4能力提升：1-2-2 同角三角函数的基本关系

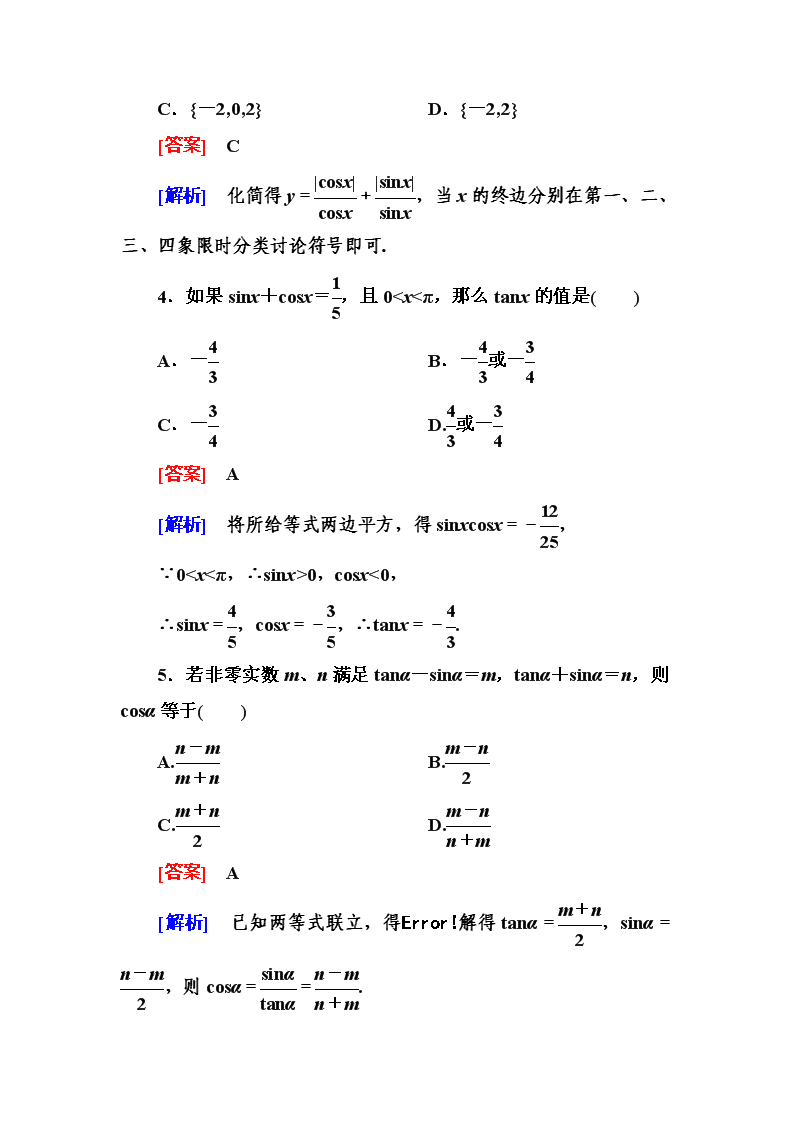
高一数学（人教A版）必修4能力提升：1-2-2 同角三角函数的基本关系

能 力 提 升 一、选择题 ‎1．已知sinα－cosα＝－，则sinα·cosα等于(　　)‎ A. B．－ ‎ C．－ D. ‎[答案]　C ‎[解析]　将所给等式两边平方，得1－2sinαcosα＝，故sinαcosα＝－.‎ ‎2．已知A为锐角，lg(1＋cosA)＝m，lg＝n，则lgsinA的值为(　　)‎ A．m＋ B．m－n C.(m＋) D.(m－n)‎ ‎[答案]　D ‎[解析]　∵m－n＝lg(1＋cosA)＋lg(1－cosA)‎ ‎＝lg(1－cos‎2A)＝lgsin‎2A＝2 lgsinA，‎ ‎∴lgsinA＝(m－n)．‎ ‎3．函数y＝＋的值域是(　　)‎ A．{0,2} B．{－2,0}‎ C．{－2,0,2} D．{－2,2}‎ ‎[答案]　C ‎[解析]　化简得y＝＋，当x的终边分别在第一、二、三、四象限时分类讨论符号即可．‎ ‎4．如果sinx＋cosx＝，且00，cosx<0，‎ ‎∴sinx＝，cosx＝－，∴tanx＝－.‎ ‎5．若非零实数m、n满足tanα－sinα＝m，tanα＋sinα＝n，则cosα等于(　　)‎ A. B. C. D. ‎[答案]　A ‎[解析]　已知两等式联立，得解得tanα＝，sinα＝，则cosα＝＝.‎ ‎6．化简(＋)(1－cosα)的结果是(　　)‎ A．sinα B．cosα C．1＋sinα D．1＋cosα ‎[答案]　A 二、填空题 ‎7．在△ABC中，sinA＝，则∠A＝________.‎ ‎[答案]　60°‎ ‎[解析]　∵2sin‎2A＝3cosA，∴2(1－cos‎2A)＝3cosA，即(2cosA－1)(cosA＋2)＝0，∴cosA＝，cosA＝－2(舍去)，∴A＝60°.‎ ‎8．已知tanα＝cosα，那么sinα＝________.‎ ‎[答案]　 ‎[解析]　由于tanα＝＝cosα，则sinα＝cos2α，所以sinα＝1－sin2α，解得sinα＝.‎ 又sinα＝cos2α≥0，所以sinα＝.‎ 三、解答题 ‎9．已知cosα＝－，且tanα>0，求的值．‎ ‎[解析]　∵cosα＝－，且tanα>0，‎ ‎∴α是第三象限角，‎ ‎∴sinα＝－＝－，‎ ＝＝ ‎＝sinα(1＋sinα)＝－×(1－)‎ ‎＝－.‎ ‎10．已知2cos2α＋3cosαsinα－3sin2α＝1，‎ 求(1)tanα；‎ ‎(2).‎ ‎[解析]　(1)2cos2α＋3cosαsinα－3sin2α＝ ‎＝，‎ 则＝1，‎ 即4tan2α－3tanα－1＝0.‎ 解得tanα＝－或tanα＝1.‎ ‎(2)原式＝＝，‎ 当tanα＝－时，原式＝；‎ 当tanα＝1时，原式＝.‎ ‎11．求证：sinα(1＋tanα)＋cosα(1＋)＝＋.‎ ‎[证明]　左边＝sinα(1＋)＋cosα(1＋＝sinα＋＋cos α＋ ‎＝＋ ‎＝＋＝右边．‎ 即原等式成立．‎