2014-2018年五年真题分类第二章 函数的概念与基本初等函数Ⅰ
第二章 函数的概念与基本初等函数Ⅰ
考点1 函数的概念
1.(2018全国Ⅱ,3)函数fx=ex−e−xx2的图像大致为 ( )
A. B.
C. D.
1.B ∵x≠0,f(−x)=e−x−exx2=−f(x)∴f(x)为奇函数,舍去A,∵f(1)=e−e−1>0∴舍去D;
∵f′(x)=(ex+e−x)x2−(ex−e−x)2xx4=(x−2)ex+(x+2)e−xx3∴x>2,f′(x)>0,所以舍去C;因此选B.
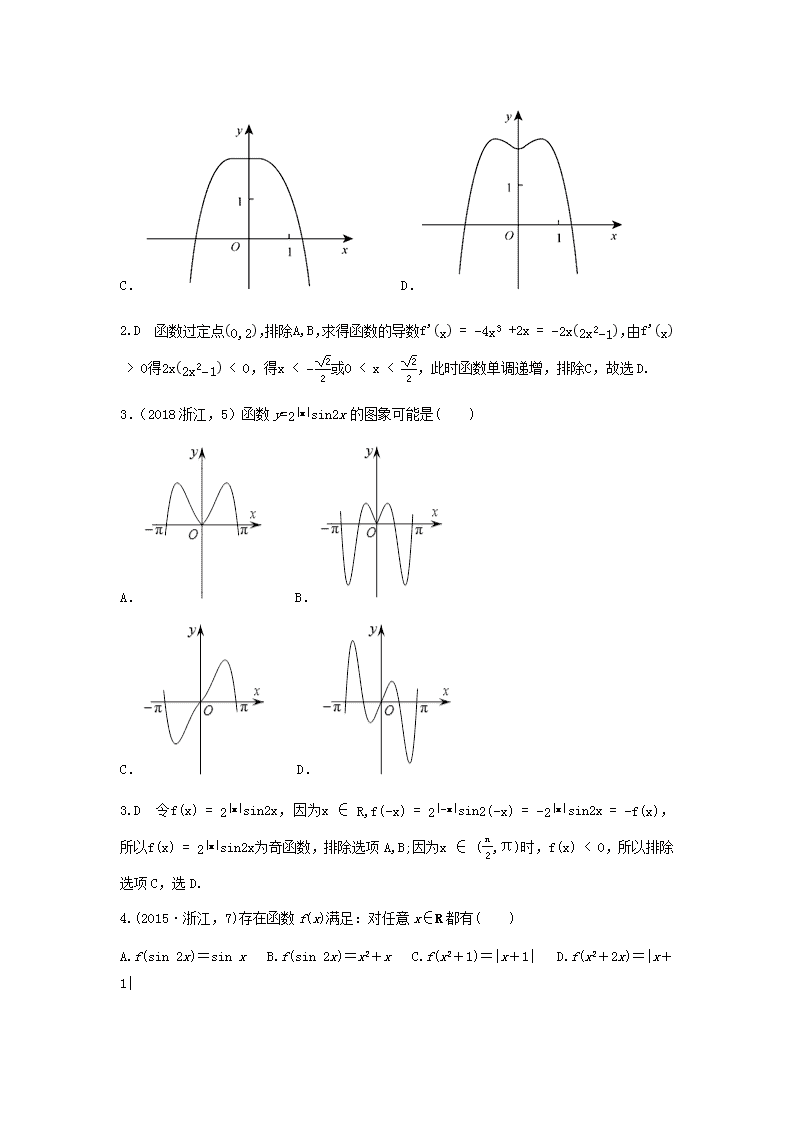
2.(2018全国Ⅲ,7)函数y=−x4+x2+2的图像大致为( )
A. B.
C. D.
2.D 函数过定点0,2,排除A,B,求得函数的导数f'x=−4x3+2x=−2x2x2−1,由f'x>0得2x2x2−1<0,得x<−22或0
0,即log2x>1或log2x<-1,解得x>2或0<x<,故所求的定义域是∪(2,+∞).]
7.(2014·江西,2)函数f(x)=ln(x2-x)的定义域为( )
A.(0,1) B.[0,1] C.(-∞,0)∪(1,+∞) D.(-∞,0]∪[1,+∞)
7.C [由题意可得x2-x>0,解得x>1或x<0,所以所求函数的定义域为(-∞,0)∪(1,+∞).]
8.(2014·江西,3)已知函数f(x)=5|x|,g(x)=ax2-x(a∈R).若f[g(1)]=1,则a=( )
A.1 B.2 C.3 D.-1
8.A [因为f[g(1)]=1,且f(x)=5|x|,所以g(1)=0,即a·12-1=0,解得a=1.]
9.(2014·安徽,9)若函数f(x)=|x+1|+|2x+a|的最小值为3,则实数a的值为( )
A.5或8 B.-1或5 C.-1或-4 D.-4或8
9.D [当a≥2时,f(x)=
如图1可知,当x=-时,f(x)min=f=-1=3,可得a=8;
当a<2时,f(x)=
如图2可知,当x=-时,f(x)min=f=-+1=3,可得a=-4.
综上可知,答案为D.]
图1 图2
10.(2014·上海,18)设f(x)=若f(0)是f(x)的最小值,则a的取值范围为( )
A.[-1,2] B.[-1,0] C.[1,2] D.[0,2]
10.D [∵当x≤0时,f(x)=(x-a)2,又f(0)是f(x)的最小值,
∴a≥0.当x>0时,f(x)=x++a≥2+a,当且仅当x=1时取“=”.要满足f(0)是f(x)的最小值,需2+a≥f(0)=a2,即a2-a-2≤0,解之,得-1≤a≤2,∴a的取值范围是0≤a≤2.选D.]
11.(2018江苏,5)函数f(x)=log2x−1的定义域为________.
11.[2,+∞) 要使函数fx有意义,则log2x−1≥0,解得x≥2,即函数fx的定义域为[2,+∞).
12.(2018江苏,9)函数f(x)满足f(x+4)=f(x)(x∈R),且在区间(−2,2]上,f(x)=cosπx2,0时,f=f,则f(6)=( )
A.-2 B.-1 C.0 D.2
5.D [当x>时,f=f,即f(x)=f(x+1),∴T=1,
∴f(6)=f(1).当x<0时,f(x)=x3-1且-1≤x≤1,f(-x)=-f(x),
∴f(2)=f(1)=-f(-1)=2,故选D.]
6.(2015·天津,7)已知定义在R上的函数f(x)=2|x-m|-1(m为实数)为偶函数,记a=f(log0.53),b=(log25),c=f(2m),则a,b,c的大小关系为( )
A.a<b<c B.a<c<b C.c<a<b D.c<b<a
6.C[因为函数f(x)=2|x-m|-1为偶函数可知,m=0,
所以f(x)=2|x|-1,当x>0时,f(x)为增函数,log0.53=-log23,
∴log25>|-log0.53|>0,
∴b=f(log25)>a=f(log0.53)>c=f(2m),故选C.]
7.(2015·福建,2)下列函数为奇函数的是( )
A.y= B.y=|sin x| C.y=cos x D.y=ex-e-x
7.D [由奇函数定义易知y=ex-e-x为奇函数,故选D.]
8.(2015·广东,3)下列函数中,既不是奇函数,也不是偶函数的是( )
A.y=x+ex B.y=x+ C.y=2x+ D.y=
8.A [令f(x)=x+ex,则f(1)=1+e,f(-1)=-1+e-1,即f(-1)≠f(1),f(-1)≠-f(1),所以y=x+ex既不是奇函数也不是偶函数,而B、C、D依次是奇函数、偶函数、偶函数,故选A.]
9.(2015·安徽,2)下列函数中,既是偶函数又存在零点的是( )
A.y=cos x B.y=sin x C.y=ln x D.y=x2+1
9.A [由于y=sin x是奇函数;y=ln x是非奇非偶函数;y=x2+1是偶函数但没有零点;只有y=cos x是偶函数又有零点.]
10.(2014·北京,2)下列函数中,在区间(0,+∞)上为增函数的是( )
A.y= B.y=(x-1)2 C.y=2-x D.y=log0.5(x+1)
10.A [显然y=是(0,+∞)上的增函数;y=(x-1)2在(0,1)上是减函数,在(1,+∞)上是增函数;y=2-x=在x∈R上是减函数;y=log0.5(x+1)在(-1,+∞)上是减函数.故选A.]
11.(2014·陕西,7)下列函数中,满足“f(x+y)=f(x)f(y)”的单调递增函数是( )
A.f(x)= B.f(x)=x3 C.f(x)= D.f(x)=3x
11.D [根据各选项知,选项C、D中的指数函数满足f(x+y)=f(x)·f(y).又f(x)=3x是增函数,所以D正确.]
12.(2014·山东,5)已知实数x,y满足ax B.ln(x2+1)>ln(y2+1) C.sin x>sin y D.x3>y3
12.D [根据指数函数的性质得x>y,此时x2,y2的大小不确定,故选项A、B中的不等式不恒成立;根据三角函数的性质,选项C中的不等式也不恒成立;根据不等式的性质知,选项D中的不等式恒成立.]
13.(2014·湖南,3)已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)-g(x)=x3+x2+1,则f(1)+g(1)=( )
A.-3 B.-1 C.1 D.3
13.C [用“-x”代替“x”,得f(-x)-g(-x)=(-x)3+(-x)2+1,化简得f(x)+g(x)=-x3+x2+1,令x=1,得f(1)+g(1)=1,故选C.]
14.(2014·新课标全国Ⅰ,3)设函数f(x),g(x)的定义域都为R,且f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是( )
A.f(x)g(x)是偶函数 B.f(x)|g(x)|是奇函数 C.|f(x)|g(x)是奇函数 D.|f(x)g(x)|是奇函数
14.B [f(x)为奇函数,g(x)为偶函数,故f(x)g(x)为奇函数,f(x)|g(x)|为奇函数,|f(x)|g(x)为偶函数,|f(x)g(x)|为偶函数,故选B.]
15.(2014·湖北,10)已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=(|x-a2|+|x-2a2|-3a2).若∀x∈R,f(x-1)≤f(x),则实数a的取值范围为( )
A. B. C. D.
15.B [当x≥0时,f(x)=,又f(x)为奇函数,可得f(x)的图象如图所示,由图象可得,当x≤2a2时,f(x)max=a2,当x>2a2时,令x-3a2=a2,得x=4a2,又∀x∈R,f(x-1)≤f(x),可知4a2-(-2a2)≤1⇒a∈,选B.]
16.(2017•江苏,11)已知函数f(x)=x3﹣2x+ex﹣ ,其中e是自然对数的底数.若f(a﹣1)+f(2a2)≤0.则实数a的取值范围是________.
16. [-1, ] 函数f(x)=x3﹣2x+ex﹣ 的导数为:f′(x)=3x2﹣2+ex+ ≥﹣2+2 =0,可得f(x)在R上递增;又f(﹣x)+f(x)=(﹣x)3+2x+e﹣x﹣ex+x3﹣2x+ex﹣ =0,可得f(x)为奇函数,则f(a﹣1)+f(2a2)≤0,即有f(2a2)≤﹣f(a﹣1)=f(1﹣a),即有2a2≤1﹣a,解得﹣1≤a≤ .
17.(2017•山东,15)若函数exf(x)(e≈2.71828…是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质.下列函数中所有具有M性质的函数的序号为________.
①f(x)=2﹣x②f(x)=3﹣x③f(x)=x3④f(x)=x2+2.
17.①④ 对于①,f(x)=2﹣x , 则g(x)=exf(x)= 为实数集上的增函数;对于②,f(x)=3﹣x , 则g(x)=exf(x)= 为实数集上的减函数;
对于③,f(x)=x3 , 则g(x)=exf(x)=ex•x3 , g′(x)=ex•x3+3ex•x2=ex(x3+3x2)=ex•x2(x+3),当x<﹣3时,g′(x)<0,∴g(x)=exf(x)在定义域R上先减后增;
对于④,f(x)=x2+2,则g(x)=exf(x)=ex(x2+2),g′(x)=ex(x2+2)+2xex=ex(x2+2x+2)>0在实数集R上恒成立,∴g(x)=exf(x)在定义域R上是增函数.∴具有M性质的函数的序号为①④.
18.(2016·四川,14)已知函数f(x)是定义在R上的周期为2的奇函数,当00,则x的取值范围是________.
21.(-1,3) [由题可知,当-20.f(x-1)的图象是由f(x)的图象向右平移1个单位长度得到的,若f(x-1)>0,则-10),g(x)=logax的图象可能是( )
3.D [当a>1时,函数f(x)=xa(x>0)单调递增,函数g(x)=logax单调递增,且过点(1,0),由幂函数的图象性质可知C错;当00)单调递增,函数g(x)=logax单调递减,且过点(1,0),排除A,因此选D.]
4.(2014·辽宁,16)对于c>0,当非零实数a,b满足4a2-2ab+4b2-c=0且使|2a+b|最大时,-+的最小值为________.
4.-2 [设2a+b=t,则2a=t-b,因为4a2-2ab+4b2-c=0,所以将2a=t-b代入整理可得6b2-3tb+t2-c=0①,由Δ≥0解得-≤t≤,当|2a+b|取最大值时t=,代入①式得b=,再由2a=t-b得a=,所以-+=-+=-=-2≥-2,当且仅当c=时等号成立.]
考点4 指数与指数函数
1.(2017·天津,6)已知奇函数f(x)在R上是增函数,g(x)=xf(x).若a=g(﹣log25.1),b=g(20.8),c=g(3),则a,b,c的大小关系为( )
A、a<b<c
B、c<b<a
C、b<a<c
D、b<c<a
1.C 奇函数f(x)在R上是增函数,当x>0,f(x)>f(0)=0,且f′(x)>0,
∴g(x)=xf(x),则g′(x)=f(x)+xf′(x)>0,∴g(x)在(0,+∞)单调递增,且g(x)=xf(x)偶函数,∴a=g(﹣log25.1)=g(log25.1),则2<﹣log25.1<3,1<20.8<2,由g(x)在(0,+∞)单调递增,则g(20.8)<g(log25.1)<g(3),∴b<a<c,故选C.
2.(2017•北京,8)根据有关资料,围棋状态空间复杂度的上限M约为3361 , 而可观测宇宙中普通物质的原子总数N约为1080 , 则下列各数中与 最接近的是( )
(参考数据:lg3≈0.48)
A.1033 B.1053 C.1073 D.1093
2. D 由题意:M≈3361 , N≈1080 , 根据对数性质有:3=10lg3≈100.48 , ∴M≈3361≈(100.48)361≈10173 , ∴ ≈ =1093 , 故选D.
3.(2014·辽宁,3)已知a=,b=log2,c=,则( )
A.a>b>c B.a>c>b C.c>a>b D.c>b>a
3.C[a=2-∈(0,1),b=log2∈(-∞,0),c=log=log23∈(1,+∞),所以c>a>b.]
4.(2015·山东,14)已知函数f(x)=ax+b(a>0,a≠1) 的定义域和值域都是[-1,0],则a+b=________.
4.- [当a>1时,f(x)=ax+b在定义域上为增函数,
∴方程组无解;
当0<a<1时,f(x)=ax+b在定义域上为减函数,
∴解得∴a+b=-.]
5.(2014·上海,9)若f(x)=-,则满足f(x)<0的x的取值范围是________.
5.(0,1) [令y1=x,y2=,f(x)<0即为y1b>c B.b>a>c C.c>b>a D.c>a>b
1.D 由题意结合对数函数的性质可知:a=log2e>1,b=ln2=1log2e∈0,1,c=log1213=log23>log2e,据此可得:c>a>b.本题选择D选项.
2.(2017•新课标Ⅰ,11)设x、y、z为正数,且2x=3y=5z , 则( )
A.2x<3y<5z B.5z<2x<3y C.3y<5z<2x D.3y<2x<5z
2. D x、y、z为正数,令2x=3y=5z=k>1.lgk>0.则x= ,y= ,z= .
∴3y= ,2x= ,5z= .∵ = = , > = .∴ >lg > >0.∴3y<2x<5z.故选D.
3. (2015·湖南,5)设函数f(x)=ln(1+x)-ln(1-x),则f(x)是( )
A.奇函数,且在(0,1)上是增函数 B. 奇函数,且在(0,1)上是减函数
C. 偶函数,且在(0,1)上是增函数 D.偶函数,且在(0,1)上是减函数
3. A [易知函数定义域为(-1,1),f(-x)=ln(1-x)-ln(1+x)=-f(x),故函数f(x)为奇函数,又f(x)=ln=ln,由复合函数单调性判断方法知,f(x)在(0,1)上是增函数,故选A.]
4.(2015·陕西,9)设f(x)=ln x,0<a<b,若p=f(),q=f,r=(f(a)+f(b)),则下列关系式中正确的是( )
A.q=r<p B.q=r>p C.p=r<q D.p=r>q
4.C[∵0<a<b,∴>,
又∵f(x)=ln x在(0,+∞)上为增函数,故f>f(),即q>p.
又r=(f(a)+f(b))=(ln a+ln b)=ln a+ln b=ln(ab)=f()=p.
故p=r<q.选C.]
5.(2014·福建,4)若函数y=logax(a>0,且a≠1)的图象如图所示,则下列函数图象正确的是( )
5.B [因为函数y=logax过点(3,1),所以1=loga3,解得a=3,所以y=3-x不可能过点(1,3),排除A;y=(-x)3=-x3不可能过点(1,1),排除C;y=log3(-x)不可能过点(-3,-1),排除D.故选B.]
6.(2014·天津,4)函数f(x)=(x2-4)的单调递增区间为( )
A.(0,+∞) B.(-∞,0) C.(2,+∞) D.(-∞,-2)
6.D [函数y=f(x)的定义域为(-∞,-2)∪(2,+∞),因为函数y=f(x)是由y=logt与t=g(x)=x2-4复合而成,又y=logt在(0,+∞)上单调递减,g(x)在(-∞,-2)上单调递减,所以函数y=f(x)在(-∞,-2)上单调递增.选D.]
7.(2014·四川,9)已知f(x)=ln(1+x)-ln(1-x),x∈(-1,1).现有下列命题:
①f(-x)=-f(x);②f=2f(x);③|f(x)|≥2|x|.
其中的所有正确命题的序号是( )
A.①②③ B.②③ C.①③ D.①②
7.A [f(-x)=ln(1-x)-ln(1+x)=-f(x),故①正确;因为f(x)=ln(1+x)-ln(1-x)=ln,又当x∈(-1,1)时,∈(-1,1),所以f=ln=ln=2ln=2f(x),故②正确;当x∈[0,1)时,|f(x)|≥2|x|⇔f(x)-2x≥0,令g(x)=f(x)-2x=ln(1+x)-ln(1-x)-2x(x∈[0,1)),因为g′(x)=+-2=>0,所以g(x)在区间[0,1)上单调递增,g(x)=f(x)-2x≥g(0)=0,即f(x)≥2x,又f(x)与y=2x都为奇函数,所以|f(x)|≥2|x|成立,故③正确,故选A.]
8.(2016·浙江,12)已知a>b>1.若logab+logba=,ab=ba,则a=______,b=______.
8.4 2 [设logba=t,则t>1,因为t+=,解得t=2,所以a=b2①,因此ab=ba⇒a2b=ab2②,解得b=2,a=4.联立①②结合b>1,解得b=2,a=4.]
9.(2015·浙江,12)若a=log43,则2a+2-a=________.
9. [2a+2-a=2log43+2-log43=2log2+2log2=+=.]
10.(2015·福建,14)若函数f(x)=(a>0,且a≠1)的值域是[4,+∞),则实数a的取值范围是________.
10.(1,2] [由题意f(x)的图象如图,则
∴1<a≤2.]
11.(2014·重庆,12)函数f(x)=log2·log(2x)的最小值为________.
11.- [依题意得f(x)=log2x·(2+2log2x)=(log2x)2+log2x=-≥-,当且仅当log2x=-,即x=时等号成立,因此函数f(x)的最小值为-.]
考点6 函数与方程
1.(2018全国Ⅰ,9)已知函数f(x)=ex,x≤0,lnx,x>0, g(x)=f(x)+x+a.若g(x)存在2个零点,则a的取值范围是( )
A.[–1,0) B.[0,+∞) C.[–1,+∞) D.[1,+∞)
1.C 画出函数f(x)的图像,y=ex在y轴右侧的去掉,再画出直线y=−x,之后上下移动,
可以发现当直线过点A时,直线与函数图像有两个交点,并且向下可以无限移动,都可以保证直线与函数的图像有两个交点,即方程f(x)=−x−a有两个解,也就是函数g(x)有两个零点,此时满足−a≤1,即a≥−1,故选C.
2.(2017•新课标Ⅲ,11)已知函数f(x)=x2﹣2x+a(ex﹣1+e﹣x+1)有唯一零点,则a=( )
A.﹣ B. C. D. 1
2. C 因为f(x)=x2﹣2x+a(ex﹣1+e﹣x+1)=﹣1+(x﹣1)2+a(ex﹣1+ )=0,
所以函数f(x)有唯一零点等价于方程1﹣(x﹣1)2=a(ex﹣1+ )有唯一解,
等价于函数y=1﹣(x﹣1)2的图象与y=a(ex﹣1+ )的图象只有一个交点.
①当a=0时,f(x)=x2﹣2x≥﹣1,此时有两个零点,矛盾;
②当a<0时,由于y=1﹣(x﹣1)2在(﹣∞,1)上递增、在(1,+∞)上递减,
且y=a(ex﹣1+ )在(﹣∞,1)上递增、在(1,+∞)上递减,
所以函数y=1﹣(x﹣1)2的图象的最高点为A(1,1),y=a(ex﹣1+ )的图象的最高点为B(1,2a),
由于2a<0<1,此时函数y=1﹣(x﹣1)2的图象与y=a(ex﹣1+ )的图象有两个交点,矛盾;
③当a>0时,由于y=1﹣(x﹣1)2在(﹣∞,1)上递增、在(1,+∞)上递减,
且y=a(ex﹣1+ )在(﹣∞,1)上递减、在(1,+∞)上递增,
所以函数y=1﹣(x﹣1)2的图象的最高点为A(1,1),y=a(ex﹣1+ )的图象的最低点为B(1,2a),
由题可知点A与点B重合时满足条件,即2a=1,即a= ,符合条件;
综上所述,a= ,故选C.
3.(2015·山东,10)设函数f(x)=则满足f(f(a))=2f(a)的a取值范围是( )
A. B.[0,1] C. D.[1, +∞)
3.C[当a=2时,f(a)=f(2)=22=4>1,f(f(a))=2f(a),
∴a=2满足题意,排除A,B选项;当a=时,f(a)=f=3×-1=1,f(f(a))=2f(a),∴a=满足题意,排除D选项,故答案为C.]
4.(2015·天津,8)已知函数f(x)=函数g(x)=b-f(2-x),其中b∈R,若函数y=f(x)-g(x)恰有4个零点,则b的取值范围是( )
A. B. C. D.
4.D [记h(x)=-f(2-x)在同一坐标系中作出f(x)与h(x)的图象如图,直线AB:y=x-4,当直线l∥AB且与f(x)的图象相切时,由
解得b′=-,--(-4)=,
所以曲线h(x)向上平移个单位后,所得图象与f(x)的图象有四个公共点,平移2个单位后,两图象有无数个公共点,因此,当<b<2时,f(x)与g(x)的图象有四个不同的交点,即y=f
(x)-g(x)恰有4个零点.选D.]
5.(2014·湖南,10)已知函数f(x)=x2+ex-(x<0)与g(x)=x2+ln(x+a)的图象上存在关于y轴对称的点,则a的取值范围是( )
A. B. C. D.
5.B [由题意可得,当x>0时,y=f(-x)与y=g(x)的图象有交点,即g(x)=f(-x)有正解,即x2+ln(x+a)=(-x)2+e-x-有正解,即e-x-ln(x+a)-=0有正解,令F(x)=e-x-ln(x+a)-,则F′(x)=-e-x-<0,故函数F(x)=e-x-ln(x+a)-在(0,+∞)上是单调递减的,要使方程g(x)=f(-x)有正解,则存在正数x使得F(x)≥0,即e-x-ln(x+a)-≥0,所以a≤,又y=在(0,+∞)上单调递减,所以a<=,选B.]
6.(2018天津,14)已知a>0,函数f(x)=x2+2ax+a, x≤0,−x2+2ax−2a,x>0.若关于x的方程f(x)=ax恰有2个互异的实数解,则a的取值范围是______________.
6.(4 , 8) 分类讨论:当x≤0时,方程fx=ax即x2+2ax+a=ax,整理可得:x2=−ax+1,很明显x=−1不是方程的实数解,则a=−x2x+1,当x>0时,方程fx=ax即−x2+2ax−2a=ax,整理可得:x2=ax−2,很明显x=2不是方程的实数解,则a=x2x−2,
令gx=−x2x+1,x≤0x2x−2,x>0,其中−x2x+1=−x+1+1x+1−2,x2x−2=x−2+4x−2+4,原问题等价于函数gx与函数y=a有两个不同的交点,求a的取值范围.结合对勾函数和函数图象平移的规律绘制函数gx的图象,同时绘制函数y=a的图象如图所示,考查临界条件,结合a>0观察可得,实数a的取值范围是4,8.
7.(2018浙江,15)已知λ∈R,函数f(x)=x−4,x≥λx2−4x+3,x<λ,当λ=2时,不等式f(x)<0的解集是___________.若函数f(x)恰有2个零点,则λ的取值范围是___________.
7. (1,4) (1,3]∪(4,+∞) 由题意得x≥2x−4<0或x<2x2−4x+3<0,所以2≤x<4或14时,f(x)=x−4>0,此时f(x)=x2−4x+3=0,x=1,3,即在(−∞,λ)上有两个零点;当λ≤4时,f(x)=x−4=0,x=4,由f(x)=x2−4x+3在(−∞,λ)上只能有一个零点得1<λ≤3.综上,λ的取值范围为(1,3]∪(4,+∞).
8.(2018江苏,11)若函数f(x)=2x3-ax2+1(a∈R)在(0,+∞)内有且只有一个零点,则f(x)在[-1,1]上的最大值与最小值的和为__________.
8.−3 由f′x=6x2−2ax=0得x=0,x=a3,因为函数fx在(0,+∞)上有且仅有一个零点且f0=1,所以a3>0,fa3=0,因此2(a3)3−a(a3)2+1=0,a=3.从而函数fx在[−1,0]上单调递增,在[0,1]上单调递减,所以f(x)max=f0, f(x)min=min{f(−1),f(1)}=f(−1),f(x)max+f(x)min= f0+f(−1)=1−4=−3.
9.(2016·山东,15)已知函数f(x)=其中m>0,若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是________.
9.(3,+∞) [如图,当x≤m时,f(x)=|x|;当x>m时,f(x)=x2-2mx+4m,在(m,+∞)为增函数,若存在实数b,使方程f(x)=b有三个不同的根,则m2-2m·m+4m<|m|.
∵m>0,∴m2-3m>0,解得m>3.
10.(2015·湖南,15)已知函数f(x)=若存在实数b,使函数g(x)=f(x)-b有两个零点,则a的取值范围是________.
10.(-∞,0)∪(1,+∞) [若0≤a≤1时,函数f(x)=在R上递增,若a>1或a<0时,
由图象知y=f(x)-b存在b使之有两个零点,故a∈(-∞,0)∪(1,+∞).]
11.(2015·安徽,15)设x3+ax+b=0,其中a,b均为实数,下列条件中,使得该三次方程仅有一个实根的是________(写出所有正确条件的编号).
①a=-3,b=-3;②a=-3,b=2;③a=-3,b>2;④a=0,b=2;⑤a=1,b=2.
11 .①③④⑤ [令f(x)=x3+ax+b,f′(x)=3x2+a,
当a≥0时,f′(x)≥0,f(x)单调递增,必有一个实根,④⑤正确;
当a<0时,由于选项当中a=-3,∴只考虑a=-3这一种情况,f′(x)=3x2-3=3(x+1)(x-1),∴f(x)极大=f(-1)=-1+3+b=b+2,f(x)极小=f(1)=1-3+b=b-2,要有一根,f(x)极大<0或f(x)极小>0,∴b<-2或b>2,①③正确,所有正确条件为①③④⑤.]
12.(2015·江苏,13)已知函数f(x)=|lnx|,g(x)=则方程|f(x)+g(x)|=1实根的个数为________.
12.4 [令h(x)=f(x)+g(x),则h(x)=当1<x<2时,h′(x)=-2x+=<0,故当1<x<2时h(x)单调递减,在同一坐标系中画出y=|h(x)|和y=1的图象如图所示.
由图象可知|f(x)+g(x)|=1的实根个数为4.]
13.(2015·北京,14)设函数f(x)=
(1)若a=1,则f(x)的最小值为________;
(2)若f(x)恰有2个零点,则实数a的取值范围是________.
13.(1)-1 (2)∪[2,+∞)[(1)当a=1时,f(x)=
当x<1时,2x-1>-1.
当x≥1时,且当x=时,f(x)min=f=-1,∴f(x)最小值为-1.
(2)1°当a≤0时,2x-a>0,
由4(x-a)(x-2a)=0得x=a或x=2a.a∉[1,+∞),
2a∉[1,+∞),
∴此时f(x)无零点.
2°当00,对任意a>0,b>0,若经过点(a,f(a)),(b,-f(b))的直线与x轴的交点为(c,0),则称c为a,b关于函数f(x)的平均数,记为Mf(a,b).例如,当f(x)=1(x>0)时,可得Mf(a,b)=c=,即Mf(a,b)为a,b的算术平均数.
(1)当f(x)=________(x>0)时,Mf(a,b)为a,b的几何平均数.
(2)当f(x)=________(x>0)时,Mf(a,b)为a,b的调和平均数.
(以上两空各只需写出一个符合要求的函数即可)
8.(1) (2)x [过点(a,f(a)),(b,-f(b))的直线的方程为y-f(a)=(x-a),
令y=0得c=.
(1)令几何平均数=⇒f(a)+f(b)=bf(a)+af(b),可取f(x)=(x>0);
(2)令调和平均数=⇒=,可取f(x)=x(x>0).]
9.(2014·山东,15)已知函数y=f(x)(x∈R),对函数y=g(x)(x∈I),定义g(x)关于f(x)的“对称函数”为函数y=h(x)(x∈I),y=h(x)满足:对任意x∈I,两个点(x,h(x)),(x,g(x))关于点(x,f(x))对称.若h(x)是g(x)=关于f(x)=3x+b的“对称函数”,且h(x)>g(x)恒成立,则实数b的取值范围是________.
9.(2,+∞) [函数g(x)的定义域是[-2,2],根据已知得=f(x),所以h(x)=2f(x)-g(x)=6x+2b-.h(x)>g(x)恒成立,即6x+2b->恒成立,即3x+b>恒成立,令y=3x+b,y=,则只要直线y=3x+b在半圆x2+y2=4(y≥0)上方即可,由>2,解得b>2(舍去负值),故实数b的取值范围是(2,+∞).]