2020届二轮复习函数A学案（全国通用）

2020届二轮复习函数A学案（全国通用）

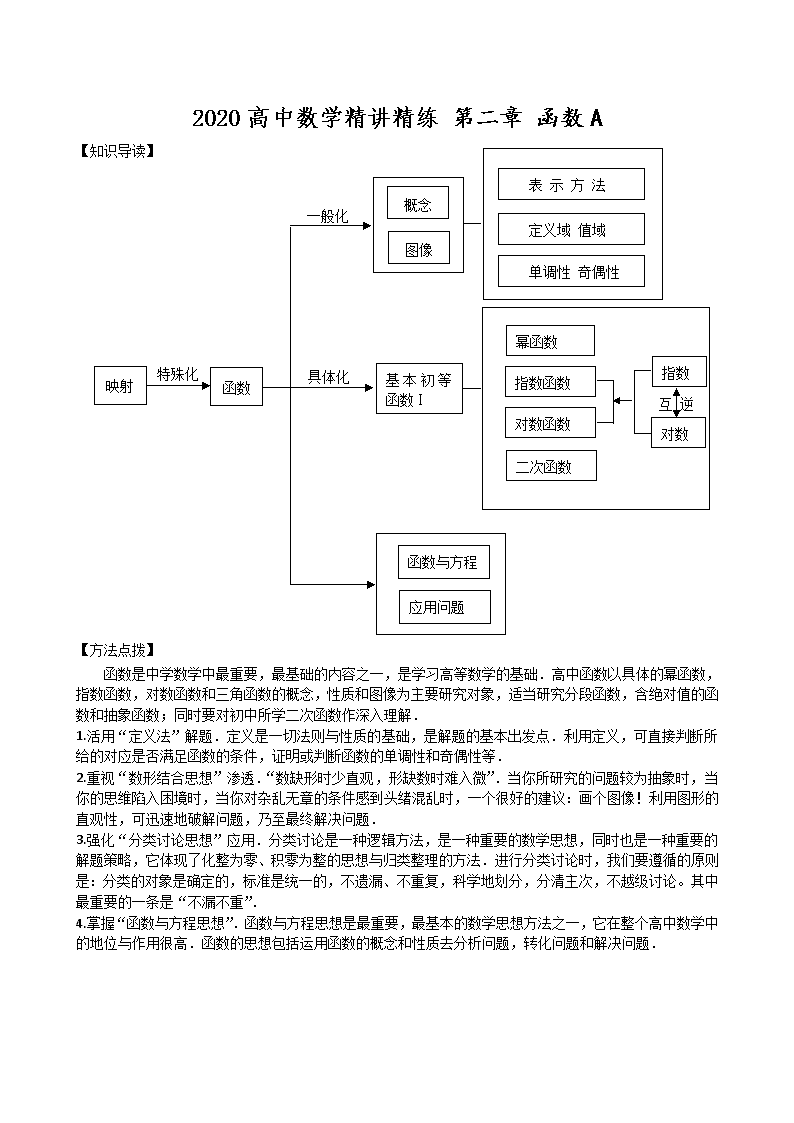
‎2020高中数学精讲精练 第二章 函数A 映射 特殊化 函数 具体化 一般化 概念 图像 表 示 方 法 定义域 值域 单调性 奇偶性 基本初等函数Ⅰ 幂函数 指数函数 对数函数 二次函数 指数 对数 互 逆 函数与方程 应用问题 ‎【知识导读】‎ ‎【方法点拨】‎ 函数是中学数学中最重要，最基础的内容之一，是学习高等数学的基础．高中函数以具体的幂函数，指数函数，对数函数和三角函数的概念，性质和图像为主要研究对象，适当研究分段函数，含绝对值的函数和抽象函数；同时要对初中所学二次函数作深入理解．‎ ‎1.活用“定义法”解题．定义是一切法则与性质的基础，是解题的基本出发点．利用定义，可直接判断所给的对应是否满足函数的条件，证明或判断函数的单调性和奇偶性等．‎ ‎2.重视“数形结合思想”渗透．“数缺形时少直观，形缺数时难入微”．当你所研究的问题较为抽象时，当你的思维陷入困境时，当你对杂乱无章的条件感到头绪混乱时，一个很好的建议：画个图像！利用图形的直观性，可迅速地破解问题，乃至最终解决问题．‎ ‎3.强化“分类讨论思想”应用．分类讨论是一种逻辑方法，是一种重要的数学思想，同时也是一种重要的解题策略，它体现了化整为零、积零为整的思想与归类整理的方法．进行分类讨论时，我们要遵循的原则是：分类的对象是确定的，标准是统一的，不遗漏、不重复，科学地划分，分清主次，不越级讨论。其中最重要的一条是“不漏不重”．‎ ‎4.掌握“函数与方程思想”．函数与方程思想是最重要，最基本的数学思想方法之一，它在整个高中数学中的地位与作用很高．函数的思想包括运用函数的概念和性质去分析问题，转化问题和解决问题．‎ 第1课 函数的概念 ‎【考点导读】‎ ‎1.在体会函数是描述变量之间的依赖关系的重要数学模型的基础上，通过集合与对应的语言刻画函数，体会对应关系在刻画函数概念中的作用；了解构成函数的要素，会求一些简单函数的定义域和值域．‎ ‎2.准确理解函数的概念，能根据函数的三要素判断两个函数是否为同一函数．‎ ‎【基础练习】‎ ‎1．设有函数组：①，；②，；③，；④，；⑤，．其中表示同一个函数的有___②④⑤___． ‎ y ‎1‎ ‎2‎ ‎2‎ x O ②‎ ‎1‎ ‎2‎ ‎2‎ x y O ①‎ ‎1‎ ‎2‎ ‎2‎ x O ③‎ y ‎2.设集合，，从到有四种对应如图所示：‎ ‎1‎ ‎2‎ ‎2‎ x O ④‎ y 其中能表示为到的函数关系的有_____②③____． ‎ ‎3.写出下列函数定义域：‎ ‎(1) 的定义域为______________； (2) 的定义域为______________；‎ ‎(3) 的定义域为______________； (4) 的定义域为_________________．‎ 且且 ‎4．已知三个函数:(1)； (2)； (3)．写出使各函数式有意义时，，的约束条件：‎ ‎ (1)______________________； (2)______________________； (3)______________________________．‎ ‎5.写出下列函数值域：‎ ‎(1) ，；值域是．‎ ‎(2) ； 值域是．‎ ‎(3) ，． 值域是．‎ ‎【范例解析】‎ 例1.设有函数组：①，；②，；‎ ‎③，；④，．其中表示同一个函数的有③④．‎ 分析：判断两个函数是否为同一函数，关键看函数的三要素是否相同．‎ 解：在①中，的定义域为，的定义域为，故不是同一函数；在②中，的定义域为，的定义域为，故不是同一函数；③④是同一函数．‎ 点评：两个函数当它们的三要素完全相同时，才能表示同一函数．而当一个函数定义域和对应法则确定时，它的值域也就确定，故判断两个函数是否为同一函数，只需判断它的定义域和对应法则是否相同即可．‎ 例2.求下列函数的定义域：① ； ② ；‎ 解：（1）① 由题意得：解得且或且，‎ 故定义域为．‎ ‎② 由题意得：，解得，故定义域为．‎ 例3.求下列函数的值域：‎ ‎（1），；‎ ‎（2）；‎ ‎（3）．‎ 分析：运用配方法，逆求法，换元法等方法求函数值域．‎ （1） 解：，，函数的值域为；‎ （2） 解法一：由，，则，，故函数值域为．‎ 解法二：由，则，，，，故函数值域为．‎ ‎（3）解：令，则，，‎ 当时，，故函数值域为．‎ 点评：二次函数或二次函数型的函数求值域可用配方法；逆求法利用函数有界性求函数的值域；用换元法求函数的值域应注意新元的取值范围．‎ ‎【反馈演练】‎ ‎1．函数f(x)＝的定义域是___________．‎ ‎2．函数的定义域为_________________．‎ ‎3. 函数的值域为________________．‎ ‎4. 函数的值域为_____________．‎ ‎5．函数的定义域为_____________________．‎ ‎6.记函数f(x)=的定义域为A，g(x)=lg[(x－a－1)(2a－x)](a<1) 的定义域为B．‎ ‎(1) 求A；‎ ‎(2) 若BA，求实数a的取值范围．‎ 解：(1)由2－≥0，得≥0，x<－1或x≥1， 即A=(－∞，－1)∪[1，+ ∞) ．‎ ‎(2) 由(x－a－1)(2a－x)>0，得(x－a－1)(x－2a)<0．‎ ‎∵a<1，∴a+1>2a，∴B=(2a，a+1) ．‎ ‎∵BA， ∴2a≥1或a+1≤－1，即a≥或a≤－2，而a<1，‎ ‎∴≤a<1或a≤－2，故当BA时， 实数a的取值范围是(－∞,－2]∪[,1)．‎ 第2课 函数的表示方法 ‎【考点导读】‎ ‎1.会根据不同的需要选择恰当的方法（如图像法，列表法，解析法）表示函数．‎ ‎2.求解析式一般有四种情况：（1）根据某个实际问题须建立一种函数关系式；（2）给出函数特征，利用待定系数法求解析式；（3）换元法求解析式；（4）解方程组法求解析式．‎ ‎【基础练习】‎ ‎1.设函数，，则_________；__________．‎ ‎2.设函数，,则_____3_______；；．‎ 第5题 ‎3.已知函数是一次函数，且，,则__15___．‎ ‎ (0≤x≤2)‎ ‎4.设f(x)＝，则f[f()]＝_____________．‎ ‎5.如图所示的图象所表示的函数解析式为__________________________．‎ ‎【范例解析】‎ 例1.已知二次函数的最小值等于4，且，求的解析式．‎ 分析：给出函数特征，可用待定系数法求解．‎ 解法一：设，则解得 故所求的解析式为．‎ 解法二：，抛物线有对称轴．故可设．‎ 将点代入解得．故所求的解析式为．‎ 解法三：设，由，知有两个根0，2，‎ 可设，，‎ 将点代入解得．故所求的解析式为．‎ 点评：三种解法均是待定系数法，也是求二次函数解析式常用的三种形式：一般式，顶点式，零点式．‎ x y O ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎60‎ 例2‎ 例2.甲同学家到乙同学家的途中有一公园，甲从家到公园的距离与乙从家到公园的距离都是2km，甲10时出发前往乙家．如图，表示甲从出发到乙家为止经过的路程y（km）与时间x（分）的关系．试写出的函数解析式．‎ 分析：理解题意，根据图像待定系数法求解析式．‎ 解：当时，直线方程为，当时，直线方程为，‎ 点评：建立函数的解析式是解决实际问题的关键，把题中文字语言描述的数学关系用数学符号语言表达．要注意求出解析式后，一定要写出其定义域．‎ ‎【反馈演练】‎ ‎1．若，，则（ D ）‎ ‎　　Ａ． 　　　　　Ｂ．　　　　Ｃ．　　Ｄ． ‎ ‎2．已知，且，则m等于________．‎ ‎3. 已知函数f(x)和g(x)的图象关于原点对称，且f(x)＝x2＋2x．求函数g(x)的解析式．‎ 解：设函数的图象上任意一点关于原点的对称点为，‎ 则 ‎∵点在函数的图象上 ‎∴．‎ 第3课 函数的单调性 ‎【考点导读】‎ ‎1.理解函数单调性，最大（小）值及其几何意义；‎ ‎2.会运用单调性的定义判断或证明一些函数的增减性．‎ ‎【基础练习】‎ ‎1.下列函数中： ‎ ‎①； ②； ③； ④．‎ 其中，在区间(0，2)上是递增函数的序号有___②___．‎ ‎2.函数的递增区间是___ R ___．‎ ‎3.函数的递减区间是__________．‎ ‎4.已知函数在定义域R上是单调减函数，且，则实数a的取值范围__________．‎ ‎5.已知下列命题：‎ ‎①定义在上的函数满足，则函数是上的增函数；‎ ‎②定义在上的函数满足，则函数在上不是减函数；‎ ‎③定义在上的函数在区间上是增函数，在区间上也是增函数，则函数在上是增函数；‎ ‎④定义在上的函数在区间上是增函数，在区间上也是增函数，则函数在上是增函数．‎ 其中正确命题的序号有_____②______．‎ ‎【范例解析】‎ 例 . 求证：（1）函数在区间上是单调递增函数；‎ ‎（2）函数在区间和上都是单调递增函数．‎ 分析：利用单调性的定义证明函数的单调性，注意符号的确定．‎ 证明：（1）对于区间内的任意两个值，，且，‎ 因为 ‎，‎ 又，则，，得，‎ 故，即，即．‎ 所以，函数在区间上是单调增函数．‎ ‎（2）对于区间内的任意两个值，，且，‎ 因为，‎ 又，则，，得，‎ 故，即，即．‎ 所以，函数在区间上是单调增函数．‎ 同理，对于区间，函数是单调增函数；‎ 所以，函数在区间和上都是单调增函数．‎ 点评：利用单调性定义证明函数的单调性，一般分三步骤：（1）在给定区间内任意取两值，；（2）作差，化成因式的乘积并判断符号；（3）给出结论．‎ 例2.确定函数的单调性．‎ 分析：作差后，符号的确定是关键．‎ 解：由，得定义域为．对于区间内的任意两个值，，且，‎ 则 又，，‎ ‎，即．‎ 所以，在区间上是增函数．‎ 点评：运用有理化可以对含根号的式子进行符号的确定．‎ ‎【反馈演练】‎ ‎1．已知函数，则该函数在上单调递__减__，（填“增”“减”）值域为_________．‎ ‎2．已知函数在上是减函数，在上是增函数，则__25___.‎ ‎3. 函数的单调递增区间为.‎ ‎4. 函数的单调递减区间为． ‎ ‎5. 已知函数在区间上是增函数，求实数a的取值范围．‎ 解：设对于区间内的任意两个值，，且，‎ 则，‎ ‎，，得，，，即．‎ 第4课 函数的奇偶性 ‎【考点导读】‎ ‎1.了解函数奇偶性的含义，能利用定义判断一些简单函数的奇偶性；‎ ‎2.定义域对奇偶性的影响：定义域关于原点对称是函数为奇函数或偶函数的必要但不充分条件；不具备上述对称性的，既不是奇函数，也不是偶函数．‎ ‎【基础练习】‎ ‎1.给出4个函数：①；②；③；④．‎ 其中奇函数的有___①④___；偶函数的有____②____；既不是奇函数也不是偶函数的有____③____．‎ ‎2. 设函数为奇函数，则实数 －1 ． ‎ ‎3.下列函数中，在其定义域内既是奇函数又是减函数的是（ A ）‎ A. B. C. D.‎ ‎【范例解析】‎ 例1.判断下列函数的奇偶性：‎ ‎（1）； （2）； ‎ ‎（3）； （4）；‎ ‎（5）； （6）‎ 分析：判断函数的奇偶性，先看定义域是否关于原点对称，再利用定义判断．‎ 解：（1）定义域为，关于原点对称；,‎ 所以为偶函数．‎ ‎（2）定义域为，关于原点对称；，‎ ‎，故为奇函数．‎ ‎（3）定义域为，关于原点对称；，且 ‎，‎ 所以既为奇函数又为偶函数．‎ ‎（4）定义域为，不关于原点对称；故既不是奇函数也不是偶函数．‎ ‎（5）定义域为，关于原点对称；，，则且，故既不是奇函数也不是偶函数．‎ ‎（6）定义域为，关于原点对称；‎ ‎，又，‎ ‎，故为奇函数．‎ 点评：判断函数的奇偶性，应首先注意其定义域是否关于原点对称；其次，利用定义即或判断，注意定义的等价形式或．‎ 例2. 已知定义在上的函数是奇函数，且当时，，求函数的解析式，并指出它的单调区间．‎ 分析：奇函数若在原点有定义，则． ‎ 解：设，则，．‎ 又是奇函数，，．‎ 当时，．‎ 综上，的解析式为．‎ 作出的图像，可得增区间为，，减区间为，．‎ 点评：（1）求解析式时的情况不能漏；（2）两个单调区间之间一般不用“”连接；（3）利用奇偶性求解析式一般是通过“”实现转化；（4）根据图像写单调区间． ‎ ‎【反馈演练】‎ ‎1．已知定义域为R的函数在区间上为减函数，且函数为偶函数，则（ D ）‎ A． B． C． D．‎ ‎2. 在上定义的函数是偶函数，且，若在区间是减函数，则函数（ B ）‎ A.在区间上是增函数，区间上是增函数 B.在区间上是增函数，区间上是减函数 C.在区间上是减函数，区间上是增函数 D.在区间上是减函数，区间上是减函数 ‎3. 设，则使函数的定义域为R且为奇函数的所有的值为____1，3 ___．‎ ‎4．设函数为奇函数，则________．‎ ‎5．若函数是定义在R上的偶函数，在上是减函数，且，则使得的x的取 值范围是（－2，2）． ‎ ‎6. 已知函数是奇函数．又，,求a，b，c的值；‎ 解：由，得，得．又，得，‎ 而，得，解得．又，或1．‎ 若，则，应舍去；若，则．‎ 所以，．‎ 综上，可知的值域为．‎ 第5 课 函数的图像 ‎【考点导读】‎ ‎1.掌握基本初等函数的图像特征，学会运用函数的图像理解和研究函数的性质；‎ ‎2.掌握画图像的基本方法：描点法和图像变换法．‎ ‎【基础练习】‎ 向上平移3个单位 向右平移1个单位 ‎1.根据下列各函数式的变换，在箭头上填写对应函数图像的变换：‎ 向右平移3个单位 作关于y轴对称的图形 ‎（1） ；‎ ‎（2） ．‎ ‎2.作出下列各个函数图像的示意图：‎ ‎（1）； （2）； （3）．‎ 解：（1）将的图像向下平移1个单位，可得的图像．图略；‎ ‎（2）将的图像向右平移2个单位，可得的图像．图略；‎ O y x ‎1‎ ‎－1‎ ‎（3）由，将的图像先向右平移1个单位，得的图像，再向下平移1个单位，可得的图像．如下图所示：‎ ‎3.作出下列各个函数图像的示意图：‎ ‎（1）； （2）； （3）； （4）．‎ 解：（1）作的图像关于y轴的对称图像，如图1所示；‎ ‎（2）作的图像关于x轴的对称图像，如图2所示；‎ ‎（3）作的图像及它关于y轴的对称图像，如图3所示；‎ ‎－1‎ O y x 图1‎ ‎（4）作的图像，并将x轴下方的部分翻折到x轴上方，如图4所示．‎ ‎－1‎ O y x 图2‎ ‎－1‎ O y x 图4‎ ‎－1‎ O y x 图3‎ ‎1‎ ‎4. 函数的图象是 （ B ）‎ A ‎1‎ x y O B ‎1‎ x y O C ‎1‎ x y O D ‎1‎ x y O ‎-1‎ ‎-1‎ ‎-1‎ ‎-1‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎【范例解析】‎ 例1.作出函数及，，，，的图像．‎ 分析：根据图像变换得到相应函数的图像．‎ 解：与的图像关于y轴对称；‎ 与的图像关于x轴对称；‎ 将的图像向左平移2个单位得到的图像；‎ 保留的图像在x轴上方的部分，将x轴下方的部分关于x轴翻折上去，并去掉原下方的部分；‎ 将的图像在y轴右边的部分沿y轴翻折到y轴的左边部分替代原y轴左边部分，并保留在y轴右边部分．图略．‎ 点评：图像变换的类型主要有平移变换，对称变换两种．平移变换：左“+”右“－”，上“+”下“－”；对称变换：与的图像关于y轴对称；‎ 与的图像关于x轴对称；与的图像关于原点对称；‎ 保留的图像在x轴上方的部分，将x轴下方的部分关于x轴翻折上去，并去掉原下方的部分；‎ 将的图像在y轴右边的部分沿y轴翻折到y轴的左边部分替代原y轴左边部分，并保留在y轴右边部分．‎ 例2.设函数.‎ ‎（1）在区间上画出函数的图像；‎ ‎（2）设集合. 试判断集合和之间的关系，并给出证明.‎ 分析：根据图像变换得到的图像，第（3）问实质是恒成立问题．‎ 解：（1）‎ ‎（2）方程的解分别是和，由于在和上单调递减，在和上单调递增，因此.‎ 由于.‎ ‎【反馈演练】‎ O y ‎1‎ ‎1‎ B．‎ x O y x ‎1‎ ‎1‎ A．‎ ‎1．函数的图象是（ B ）‎ ‎ ‎ O y ‎－1‎ ‎1‎ D．‎ x O y x ‎－1‎ ‎1‎ C．‎ ‎2. 为了得到函数的图象，可以把函数的图象向右平移1个单位长度得到．‎ ‎3．已知函数的图象有公共点A，且点A的横坐标为2，则=．‎ ‎4．设f(x)是定义在R上的奇函数，且y=f (x)的图象关于直线对称，则 f (1)+ f (2)+ f (3)+ f (4)+ f (5)=_____0____ ．‎ ‎5. 作出下列函数的简图：‎ ‎（1）； （2）； （3）．‎