2019届二轮复习同角三角比教案（全国通用）

2019届二轮复习同角三角比教案（全国通用）

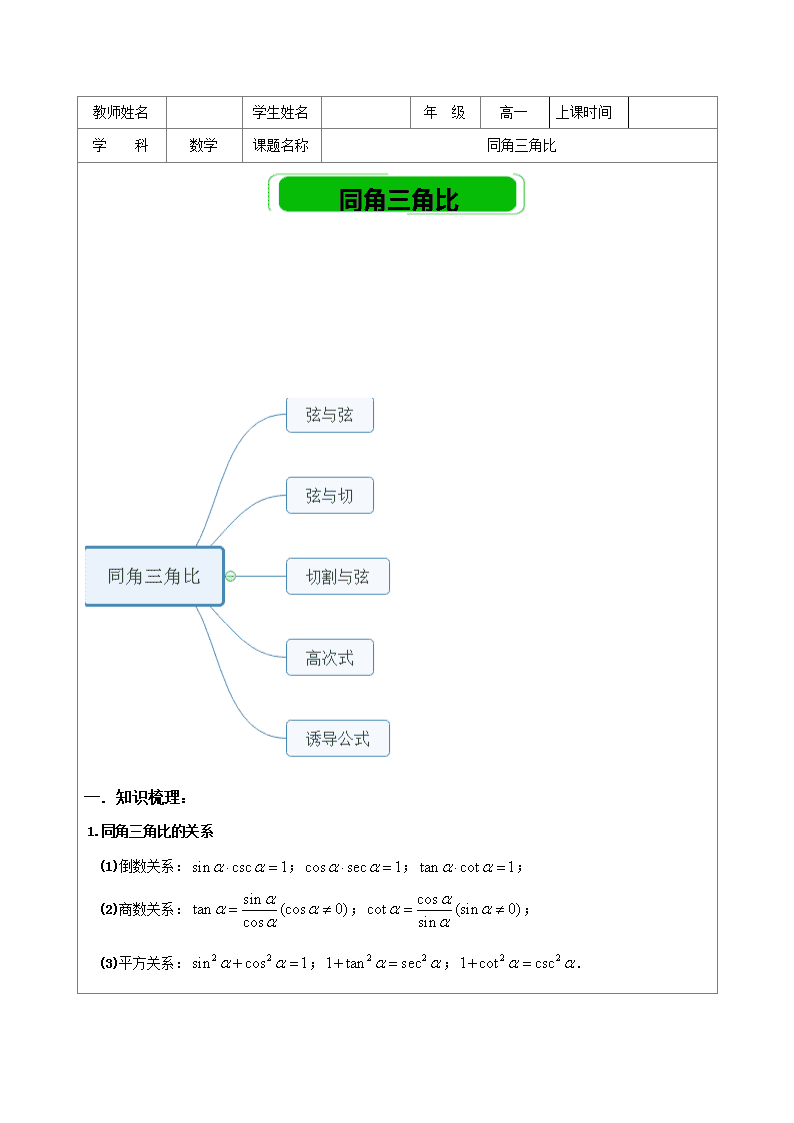
教师姓名 ‎ ‎ 学生姓名 ‎ ‎ 年 级 高一 上课时间 ‎ ‎ 学 科 数学 课题名称 ‎ 同角三角比 同角三角比 一．知识梳理：‎ ‎1.同角三角比的关系 ‎(1)倒数关系：；；；‎ ‎(2)商数关系：；；‎ ‎(3)平方关系：；；.‎ ‎ (4)这些关系式还可以如图样加强形象记忆： ‎① 对角线上两个函数的乘积为1(倒数关系).‎ ‎②任一角的函数等于与其相邻的两个函数的积(商数关系).‎ ‎③阴影部分，顶角两个函数的平方和等于底角函数的平方 ‎(平方关系).‎ ‎2.诱导公式 ‎ 第一组：‎ ‎ ‎ ‎ 第二组：‎ ‎ ‎ ‎ 第三组：‎ ‎ ‎ ‎ 第四组：‎ ‎ ‎ ‎ 第五组：‎ ‎ ‎ 二、例题讲解：‎ ‎1. 基础梳理1：三角比定义及计算 例1.已知，求的值． ‎ 答案：∵,　　∴是第二或第三象限角．因此要对所在象限分类．‎ 当是第二象限角时， ‎ 当是第三象限时,‎ 例2.已知角终边上一点，且，求和的值．‎ 答案：‎ 当时，；‎ 当时，；‎ 当时，．‎ ‎2. 基础梳理3：诱导公式 例3.求下列各三角比的值.‎ ‎（1）； （2）； （3）；‎ ‎（4） （5）‎ 答案：（1）（2） （3） （4）（5）‎ ‎3. 基础梳理2：公式转化 例4.如果满足条件　，则所在象限是________.‎ 答案：第二象限的角。　‎ 例5.已知是第三象限角，化简： ‎ ‎ 答案：.‎ 例6.化简下列各式：‎ ‎ ‎ ‎ ‎ 答案： （1）1 ；（2）1‎ 例7.求证：；‎ 答案：左边 ‎ 右边 ‎4. 难点分析1：弦与弦的变化 例8.求证：. ‎ 答案：证法：左边=右边，‎ 例9.化简：（1）；‎ ‎ （2）.‎ 答案： （1）. （2）.‎ 例10.若是△的一个内角，且，则的值为（ ）‎ A． B． C． D．‎ 答案：D 例11. ＝_____________.‎ 答案：sin2+cos2. ‎ 例12.已知是方程的两个根，求和的值．‎ 答案： ‎ ‎5. 难点突破2：弦与切转化 例13.已知：是三角形的内角，若的值．‎ 答案：‎ 例14.已知3sinα＝－4cosα，求 答案： 例15.已知，求 答案： ；。‎ 例16.已知,则_________.‎ 答案：1‎ ‎【解析】由已知,得,‎ ‎∴.‎ 例17.已知，求的值.‎ 答案： 原式 ‎ .‎ ‎6.综合应用 例18.已知：　　　　　．‎ 答案： ‎ ‎1.已知 ，求和。‎ 答案： ‎ 当是第一象限角时,‎ 当是第三象限角时,‎ ‎2.已知且为第四象限的角，求的其他三角比的值；‎ 答案：解：为第四象限的角，‎ ‎ ‎ ‎3.已知，求的值．‎ 答案：1‎ ‎4.方程的解集为 ．‎ 答案：‎ ‎5.（1）已知为锐角，且，求的值；‎ ‎（2）已知，且、是方程的两根，求，，的值．‎ 答案：（1）；（2），，‎