2019年相阳教育“黉门云”高考等值试卷★预测卷文数

2019年相阳教育“黉门云”高考等值试卷★预测卷文数

‎2019年相阳教育“黉门云”高考等值试卷★预测卷 文科数学（全国Ⅲ卷）‎ 注意事项：‎ ‎ 1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。‎ ‎2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。‎ ‎3．考试结束后，将本试卷和答题卡一并交回。‎ 一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。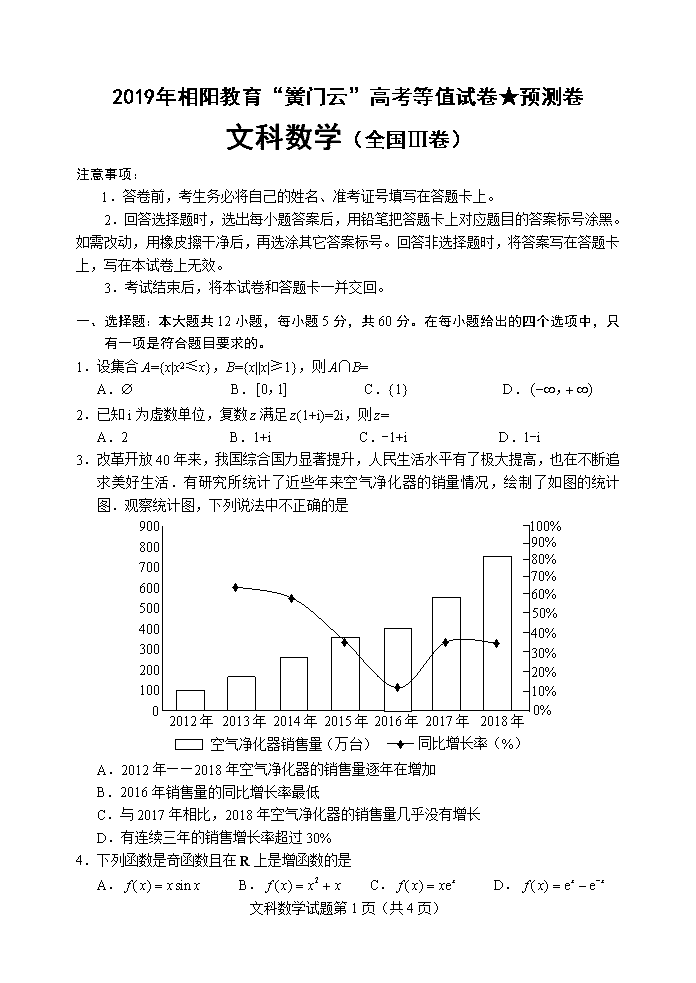‎ ‎1．设集合A={x|x2≤x}，B={x||x|≥1}，则A∩B=‎ A．Æ B． C．{1} D． ‎ ‎2．已知i为虚数单位，复数z满足z(1+i)=2i，则z=‎ A．2 B．1+i C．-1+i D．1-i ‎ ‎100‎ ‎200‎ ‎300‎ ‎400‎ ‎500‎ ‎600‎ ‎700‎ ‎800‎ ‎0‎ ‎900‎ ‎0%‎ ‎10%‎ ‎20%‎ ‎30%‎ ‎40%‎ ‎50%‎ ‎60%‎ ‎70%‎ ‎80%‎ ‎100%‎ ‎90%‎ ‎2012年 ‎2013年 ‎2014年 ‎2015年 ‎2016年 ‎2017年 ‎2018年 ‎♦‎ ‎♦‎ ‎♦‎ ‎♦‎ ‎♦‎ ‎♦‎ ‎♦‎ 空气净化器销售量（万台）‎ 同比增长率（%）‎ ‎3．改革开放40年来，我国综合国力显著提升，人民生活水平有了极大提高，也在不断追求美好生活．有研究所统计了近些年来空气净化器的销量情况，绘制了如图的统计图．观察统计图，下列说法中不正确的是 A．2012年——2018年空气净化器的销售量逐年在增加 B．2016年销售量的同比增长率最低 C．与2017年相比，2018年空气净化器的销售量几乎没有增长 D．有连续三年的销售增长率超过30%‎ ‎4．下列函数是奇函数且在R上是增函数的是 A． B． C． D．‎ 文科数学试题第4页（共4页）‎ ‎5．“0b>0)的离心率为，A、B分别为E的左顶点和上顶点，若AB的中点的纵坐标为，则E的方程为 A． B． ‎ C． D．‎ ‎7．我国古代木匠精于钻研，技艺精湛，常常设计出巧夺天工的建筑．在一座宫殿中，有一件特别的“柱脚”的三视图如右图所示，则其体积为 A．+4π B．+8π C．8+4π D．8+8π ‎8．将函数的图象向右平移(>0)个单位，再向上平移1个单位，所得图象经过点(，1)，则的最小值为 A． B． C． D． ‎ ‎9．已知双曲线(a>0，b>0)的左、右焦点分别为F1，F2，过F1作x2+y2=a2的切线，交双曲线右支于点M，若∠F1MF2=45º，则双曲线的离心率为 A．2 B．3 C． D．‎ ‎10．有一个长方体木块，三个侧面积分别为8，12，24，现将其削成一个正四面体模型，则该正四面体模型棱长的最大值为 A．2 B． C．4 D．‎ ‎11．已知在平面直角坐标系xOy中，O为坐标原点，A(0，2)，|OB|2+|OA|2=20，若平面内点P满足，则|PO|的最大值为 A．7 B．6 C．5 D．4‎ ‎12．已知函数(m∈R)存在两个极值点x1，x2(x11．‎ ‎（1）求{an}的通项公式；‎ ‎（2）记数列{}的前n项和为Tn，若4-Tn=(n+2)Sn成立，求n．‎ a ‎80‎ 年龄(岁)‎ ‎90‎ ‎100‎ ‎110‎ ‎120‎ ‎70‎ 频率 组距 ‎0.010‎ ‎0.015‎ ‎0.030‎ ‎15‎ ‎25‎ ‎35‎ ‎45‎ ‎55‎ ‎65‎ ‎18．（本小题满分12分）‎ 第十三届全国人大第二次会议于2019年3月5日在北京开幕．为广泛了解民意，某人大代表利用网站进行民意调查．数据调查显示，民生问题是百姓最为关心的热点，参与调查者中关注此问题的约占80%．现从参与调查者中随机选出200人，并将这200人按年龄分组，第1组，第2组，第3组，第4组，第5组，得到的频率分布直方图如上图所示．‎ ‎（1）求a；‎ ‎（2）现在要从年龄较小的第1组和第2组中用分层抽样的方法抽取5人，并再从这5人中随机抽取2人接受现场访谈，求这两人恰好属于不同组别的概率；‎ ‎（3）把年龄在第1，2，3组的居民称为青少年组，年龄在第4，5组的居民称为中老年组，若选出的200人中不关注民生问题的中老年人有10人，问是否有99%的把握认为是否关注民生与年龄有关？‎ 附： ‎ P(K2≥k0)‎ ‎0.150‎ ‎0.100‎ ‎0.050‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k0‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 文科数学试题第4页（共4页）‎ ‎，n=a+b+c+d．‎ ‎19．（本小题满分12分）‎ A B C D E F O 如图，在三棱柱ADE-BCF中，侧面ABCD是为菱形， E在平面ABCD内的射影O恰为线段BD的中点．‎ ‎（1）求证：AC⊥CF；‎ ‎（2）若∠BAD=60º，AE=AB=2，求四面体B-CEF的体积．‎ ‎20．（本小题满分12分）‎ 在平面直角坐标系xOy中，已知动圆M经过定点F(0，1)且与直线y+1=0相切，记动圆M的圆心M的轨迹为曲线C．‎ ‎ （1）求曲线C的方程；‎ ‎（2）设直线l与曲线C相交于M、N两点，O为坐标原点，OM、ON的斜率分别为kOM，kON，且满足kOM·kON=，△OMN的面积为8，求直线l的方程．‎ ‎21．（本小题满分12分）‎ 已知函数(a∈R)在定义域上满足≤0恒成立．‎ ‎（1）求实数a的值；‎ ‎（2）令在上的最小值为，求证：．‎ ‎（二）选考题：共10分．请考生在第22、23题中任选一题做答。如果多做，则按所做的第一题记分。‎ ‎22． [选修4—4：坐标系与参数方程]（10分）‎ 在平面直角坐标系中，P(2，0)．以坐标原点为极点，x轴正半轴为极轴建立极坐标系，已知曲线C的极坐标方程为，点Q(ρ，θ)(0≤θ≤)为C上的动点，M为PQ的中点．‎ ‎（1）请求出M点轨迹C1的直角坐标方程；‎ ‎（2）设点A的极坐标为A(1，π)，若直线l经过点A且与曲线C1交于点E，F，弦EF的中点为D，求的取值范围．‎ ‎23． [选修4—5：不等式选讲]（10分）‎ 已知a>0，b>0．‎ ‎ （1）若关于x的不等式|x+3|-|x-1|≤a2-3a对任意实数x都成立，求实数a的最小值；‎ ‎（2）求证：≥．‎ 文科数学试题第4页（共4页）‎