数学卷·2018届江西省赣州市会昌中学高二上学期第一次月考数学试卷（文科） （解析版）

数学卷·2018届江西省赣州市会昌中学高二上学期第一次月考数学试卷（文科） （解析版）

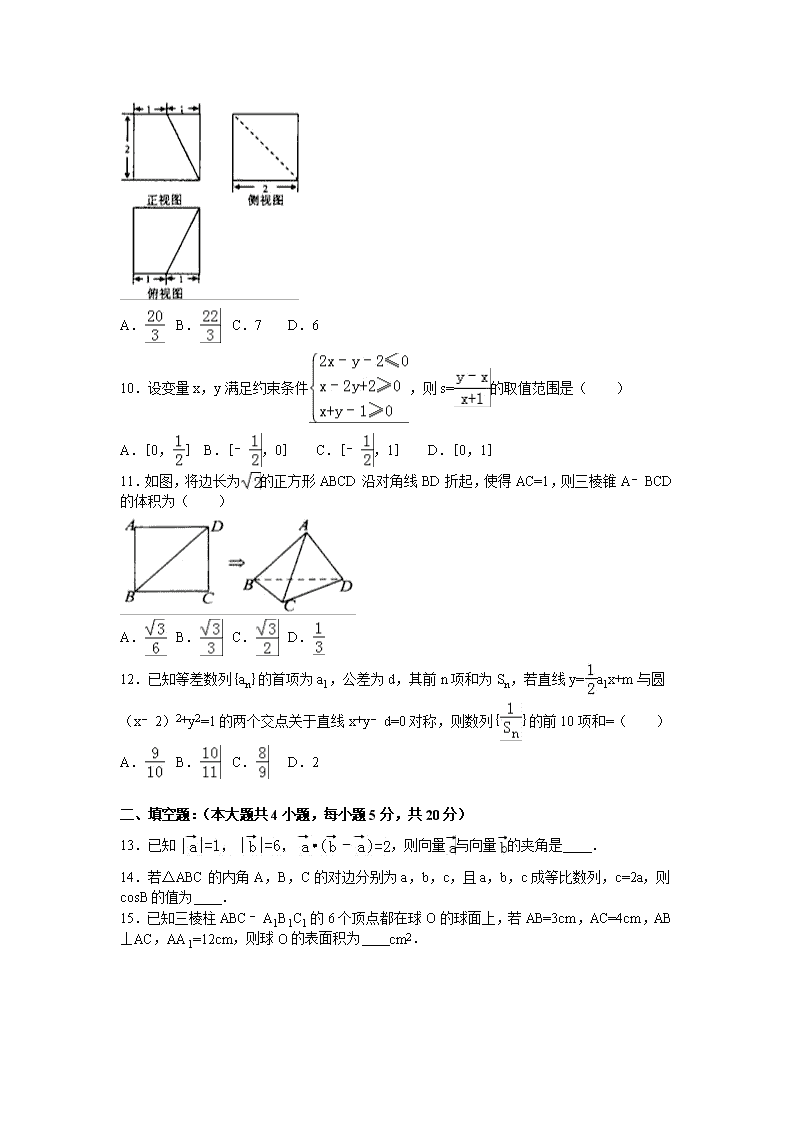
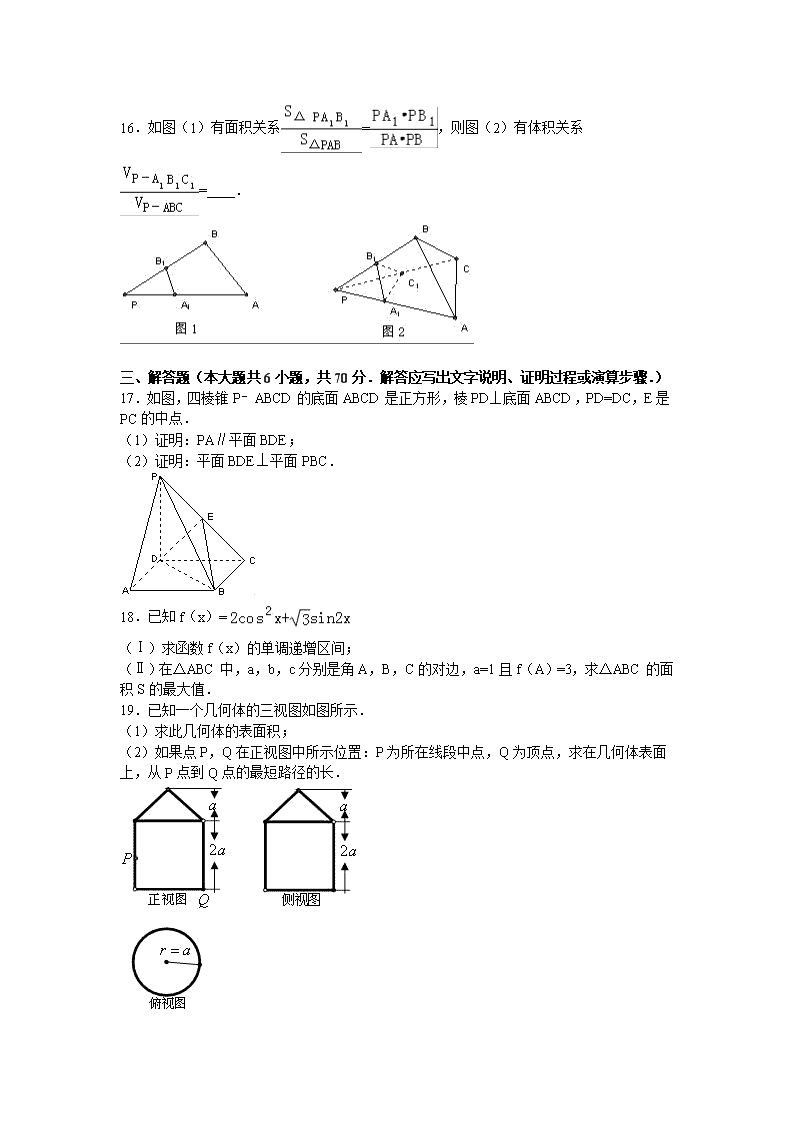
‎2016-2017学年江西省赣州市会昌中学高二（上）第一次月考数学试卷（文科）‎ ‎　‎ 一、选择题（本大题共12小题，每小题5分，共60分）‎ ‎1．设l，m是两条不同的直线，α是一个平面，则下列命题正确的是（　　）‎ A．若l⊥m，m⊂α，则l⊥α B．若l⊥α，l∥m，则m⊥α C．若l∥α，m⊂α，则l∥m D．若l∥α，m∥α，则l∥m ‎2．在等比数列{an}中，a3，a15是方程x2﹣6x+8=0的根，则的值为（　　）‎ A． B．4 C． D．±4‎ ‎3．平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为，则球O的表面积为（　　）‎ A．12π B．12π C．8π D．4π ‎4．在△ABC中，A=60°，a=，b=，则（　　）‎ A．B=45°或135° B．B=135°‎ C．B=45° D．以上答案都不对 ‎5．某校为了解本校高三学生学习心里状态，采用系统抽样方法从800人中抽取40人参加某种测试，为此将题目随机编号1，2，…，800，分组后再第一组采用简单随机抽样的方法抽到号码为18，抽到的40人中，编号落入区间[1，200]的人做试卷A，编号落入区间[201，560]的人做试卷B，其余的人做试卷C，则做试卷C的人数为（　　）‎ A．10 B．12 C．18 D．28‎ ‎6．将圆x2+y2﹣2x﹣4y+1=0平分的直线是（　　）‎ A．x+y﹣1=0 B．x+y+3=0 C．x﹣y+1=0 D．x﹣y+3=0‎ ‎7．已知向量=（3，﹣2），=（x，y﹣1）且∥，若x，y均为正数，则+的最小值是（　　）‎ A． B． C．8 D．24‎ ‎8．在正方体ABCD﹣A1B1C1D1中，点E，F分别是棱AB，BB1的中点，则异面直线EF和BC1所成的角是（　　）‎ A．60° B．45° C．90° D．120°‎ ‎9．若某几何体的三视图如图所示，则此几何体的体积是（　　）‎ A． B． C．7 D．6‎ ‎10．设变量x，y满足约束条件，则s=的取值范围是（　　）‎ A．[0，] B．[﹣，0] C．[﹣，1] D．[0，1]‎ ‎11．如图，将边长为的正方形ABCD沿对角线BD折起，使得AC=1，则三棱锥A﹣BCD的体积为（　　）‎ A． B． C． D．‎ ‎12．已知等差数列{an}的首项为a1，公差为d，其前n项和为Sn，若直线y=a1x+m与圆（x﹣2）2+y2=1的两个交点关于直线x+y﹣d=0对称，则数列{}的前10项和=（　　）‎ A． B． C． D．2‎ ‎　‎ 二、填空题：（本大题共4小题，每小题5分，共20分）‎ ‎13．已知，则向量与向量的夹角是　　．‎ ‎14．若△ABC的内角A，B，C的对边分别为a，b，c，且a，b，c成等比数列，c=2a，则cosB的值为　　．‎ ‎15．已知三棱柱ABC﹣A1B1C1的6个顶点都在球O的球面上，若AB=3cm，AC=4cm，AB⊥AC，AA1=12cm，则球O的表面积为　　cm2．‎ ‎16．如图（1）有面积关系=，则图（2）有体积关系=　　．‎ ‎　‎ 三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）‎ ‎17．如图，四棱锥P﹣ABCD的底面ABCD是正方形，棱PD⊥底面ABCD，PD=DC，E是PC的中点．‎ ‎（1）证明：PA∥平面BDE；‎ ‎（2）证明：平面BDE⊥平面PBC．‎ ‎18．已知f（x）=‎ ‎（Ⅰ）求函数f（x）的单调递增区间；‎ ‎（Ⅱ）在△ABC中，a，b，c分别是角A，B，C的对边，a=1且f（A）=3，求△ABC的面积S的最大值．‎ ‎19．已知一个几何体的三视图如图所示．‎ ‎（1）求此几何体的表面积；‎ ‎（2）如果点P，Q在正视图中所示位置：P为所在线段中点，Q为顶点，求在几何体表面上，从P点到Q点的最短路径的长．‎ ‎20．已知以点C为圆心的圆经过点A（0，1）和B（4，3），且圆心在直线3x+y﹣15=0上．‎ ‎（Ⅰ）求圆C的方程；‎ ‎（Ⅱ）设点P在圆C上，求△PAB的面积的最大值．‎ ‎21．如图AB是圆O的直径，点C是弧AB上一点，VC垂直圆O所在平面，D，E分别为VA，VC的中点．‎ ‎（1）求证：DE⊥VB；‎ ‎（2）若VC=CA=6，圆O的半径为5，求点E到平面BCD的距离．‎ ‎22．设数列{an}的各项均为正数，它的前n项的和为Sn，点（an，Sn）在函数y=x2+x+的图象上；数列{bn}满足b1=a1，bn+1（an+1﹣an）=bn．其中n∈N*．‎ ‎（Ⅰ）求数列{an}和{bn}的通项公式；‎ ‎（Ⅱ）设cn=，求证：数列{cn}的前n项的和Tn＞（n∈N*）．‎ ‎　‎ ‎2016-2017学年江西省赣州市会昌中学高二（上）第一次月考数学试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题（本大题共12小题，每小题5分，共60分）‎ ‎1．设l，m是两条不同的直线，α是一个平面，则下列命题正确的是（　　）‎ A．若l⊥m，m⊂α，则l⊥α B．若l⊥α，l∥m，则m⊥α C．若l∥α，m⊂α，则l∥m D．若l∥α，m∥α，则l∥m ‎【考点】直线与平面平行的判定．‎ ‎【分析】根据题意，依次分析选项：A，根据线面垂直的判定定理判断．C：根据线面平行的判定定理判断．D：由线线的位置关系判断．B：由线面垂直的性质定理判断；综合可得答案．‎ ‎【解答】解：A，根据线面垂直的判定定理，要垂直平面内两条相交直线才行，不正确；‎ C：l∥α，m⊂α，则l∥m或两线异面，故不正确．‎ D：平行于同一平面的两直线可能平行，异面，相交，不正确．‎ B：由线面垂直的性质可知：平行线中的一条垂直于这个平面则另一条也垂直这个平面．故正确．‎ 故选B ‎　‎ ‎2．在等比数列{an}中，a3，a15是方程x2﹣6x+8=0的根，则的值为（　　）‎ A． B．4 C． D．±4‎ ‎【考点】等比数列的通项公式．‎ ‎【分析】利用一元二次方程的根与系数的关系、等比数列的通项公式及其性质即可得出．‎ ‎【解答】解：∵a3，a15是方程x2﹣6x+8=0的根，‎ ‎∴a3=2，a15=4；或a3=4，a15=2．‎ 可知a1q2=2，a1＞0．‎ ‎∴=．‎ 则==a9=2．‎ 故选：A．‎ ‎　‎ ‎3．平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为，则球O的表面积为（　　）‎ A．12π B．12π C．8π D．4π ‎【考点】球的体积和表面积．‎ ‎【分析】根据球心到平面的距离结合球的截面圆性质，利用勾股定理算出球半径R的值，再根据球的表面积公式，可得球的表面积．‎ ‎【解答】解：∵平面α截球O的球面所得圆的半径为1，该平面与球心的距离d=，‎ ‎∴球半径R==‎ 根据球的表面积公式，得S=4πR2=12π 故选：B．‎ ‎　‎ ‎4．在△ABC中，A=60°，a=，b=，则（　　）‎ A．B=45°或135° B．B=135°‎ C．B=45° D．以上答案都不对 ‎【考点】正弦定理．‎ ‎【分析】由a，b及sinA的值，利用正弦定理求出sinB的值，根据a大于b，得到A大于B，即可求出B的度数．‎ ‎【解答】解：根据正弦定理=得：sinB===，‎ ‎∵b＜a，∴B＜A=60°，‎ ‎∴B=45°．‎ 故选C ‎　‎ ‎5．某校为了解本校高三学生学习心里状态，采用系统抽样方法从800人中抽取40人参加某种测试，为此将题目随机编号1，2，…，800，分组后再第一组采用简单随机抽样的方法抽到号码为18，抽到的40人中，编号落入区间[1，200]的人做试卷A，编号落入区间[201，560]的人做试卷B，其余的人做试卷C，则做试卷C的人数为（　　）‎ A．10 B．12 C．18 D．28‎ ‎【考点】系统抽样方法．‎ ‎【分析】由题意可得抽到的号码构成以18为首项、以20为公差的等差数列，求得此等差数列的通项公式为an=20n﹣2，由561≤20n﹣2≤800，求得正整数n的个数，即为所求．‎ ‎【解答】解：∵800÷40=20，‎ ‎∴由题意可得抽到的号码构成以18为首项、以20为公差的等差数列，‎ 且此等差数列的通项公式为an=18+20（n﹣1）=20n﹣2．‎ 落入区间[561，800]的人做问卷C，‎ 由561≤20n﹣2≤800，‎ ‎ 即563≤20n≤802‎ 解得28≤n≤40．‎ 再由n为正整数可得29≤n≤40，‎ ‎∴做问卷C的人数为40﹣29+1=12，‎ 故选：B．‎ ‎　‎ ‎6．将圆x2+y2﹣2x﹣4y+1=0平分的直线是（　　）‎ A．x+y﹣1=0 B．x+y+3=0 C．x﹣y+1=0 D．x﹣y+3=0‎ ‎【考点】直线与圆相交的性质．‎ ‎【分析】将圆的方程化为标准方程，找出圆心坐标，由所求直线要将圆平分，得到所求直线过圆心，故将圆心坐标代入四个选项中的直线方程中检验，即可得到满足题意的直线方程．‎ ‎【解答】解：将圆的方程化为标准方程得：（x﹣1）2+（y﹣2）2=4，‎ 可得出圆心坐标为（1，2），‎ 将x=1，y=2代入A选项得：x+y﹣1=1+2﹣1=2≠0，故圆心不在此直线上；‎ 将x=1，y=2代入B选项得：x+y+3=1+2+3=6≠0，故圆心不在此直线上；‎ 将x=1，y=2代入C选项得：x﹣y+1=1﹣2+1=0，故圆心在此直线上；‎ 将x=1，y=2代入D选项得：x﹣y+3=1﹣2+3=2≠0，故圆心不在此直线上，‎ 则直线x﹣y+1=0将圆平分．‎ 故选C ‎　‎ ‎7．已知向量=（3，﹣2），=（x，y﹣1）且∥，若x，y均为正数，则+的最小值是（　　）‎ A． B． C．8 D．24‎ ‎【考点】基本不等式；平面向量共线（平行）的坐标表示．‎ ‎【分析】利用向量共线定理可得2x+3y=3，再利用“乘1法”和基本不等式即可得出．‎ ‎【解答】解：∵，∴﹣2x﹣3（y﹣1）=0，化为2x+3y=3，‎ ‎∴+===8，当且仅当2x=3y=时取等号．‎ ‎∴+的最小值是8．‎ 故选：C．‎ ‎　‎ ‎8．在正方体ABCD﹣A1B1C1D1中，点E，F分别是棱AB，BB1的中点，则异面直线EF和BC1所成的角是（　　）‎ A．60° B．45° C．90° D．120°‎ ‎【考点】异面直线及其所成的角．‎ ‎【分析】建立空间直角坐标系，利用向量的夹角公式即可得出．‎ ‎【解答】解：如图所示，设AB=2，‎ 则A（2，0，0），B（2，2，0），B1（2，2，2），C1（0，2，2），E（2，1，0），F（2，2，1）．‎ ‎∴=（﹣2，0，2），=（0，1，1），‎ ‎∴===，‎ ‎∴=60°．‎ ‎∴异面直线EF和BC1所成的角是60°．‎ 故选：A．‎ ‎　‎ ‎9．若某几何体的三视图如图所示，则此几何体的体积是（　　）‎ A． B． C．7 D．6‎ ‎【考点】由三视图求面积、体积．‎ ‎【分析】由三视图可知：该几何体是一个正方体切去一个三棱锥所得的组合体，分别计算正方体和棱锥的体积，相减可得答案．‎ ‎【解答】解：由三视图可知：该几何体是一个正方体切去一个三棱锥所得的组合体，如下图：‎ 正方体的体积为：2×2×2=8，‎ 三棱锥的体积为：××1×2×2=，‎ 故组合体的体积V=8﹣=，‎ 故选：B ‎　‎ ‎10．设变量x，y满足约束条件，则s=的取值范围是（　　）‎ A．[0，] B．[﹣，0] C．[﹣，1] D．[0，1]‎ ‎【考点】简单线性规划．‎ ‎【分析】令y﹣x=n，x+1=m，把已知的不等式转化为关于m，n的不等式组，把s=转化为，作出关于m，n的约束条件的可行域后由斜率公式得答案．‎ ‎【解答】解：令y﹣x=n，x+1=m，‎ 则x=m﹣1，y=m+n﹣1，‎ 代入，得．‎ 作出可行域如图，‎ s=化为．‎ 分别联立方程组，‎ 解得：A（2，﹣1），C（1，1）．‎ ‎∴的范围为．‎ 故选：C．‎ ‎　‎ ‎11．如图，将边长为的正方形ABCD沿对角线BD折起，使得AC=1，则三棱锥A﹣BCD的体积为（　　）‎ A． B． C． D．‎ ‎【考点】棱柱、棱锥、棱台的体积．‎ ‎【分析】如图所示，图1中，连接AC与BD相交于点O，AC⊥BD，可得OA=OC=AC．图2中，△OAC是等边三角形，BD⊥平面OAC，利用三棱锥A﹣BCD的体积=×BD，即可得出．‎ ‎【解答】解：如图所示，图1中，连接AC与BD相交于点O，AC⊥BD，‎ 则OA=OC=AC=1，‎ 图2中，△OAC是等边三角形，OA⊥BD，OC⊥BD，‎ OA∩OC=O．‎ ‎∴BD⊥平面OAC，‎ ‎∴三棱锥A﹣BCD的体积=×BD==．‎ 故选：A．‎ ‎　‎ ‎12．已知等差数列{an}的首项为a1，公差为d，其前n项和为Sn，若直线y=a1x+m与圆（x﹣2）2+y2=1的两个交点关于直线x+y﹣d=0对称，则数列{}的前10项和=（　　）‎ A． B． C． D．2‎ ‎【考点】等差数列的性质．‎ ‎【分析】利用直线y=a1x+m与圆（x﹣2）2+y2=1的两个交点关于直线x+y﹣d=0对称，可得a1=2，d=2，利用等差数列的求和公式求出Sn，再用裂项法即可得到结论．‎ ‎【解答】解：∵直线y=a1x+m与圆（x﹣2）2+y2=1的两个交点关于直线x+y﹣d=0对称，‎ ‎∴a1=2，2﹣d=0‎ ‎∴d=2‎ ‎∴Sn==n2+n ‎∴=，‎ ‎∴数列{}的前10项和为1﹣+﹣+…+=‎ 故选：B．‎ ‎　‎ 二、填空题：（本大题共4小题，每小题5分，共20分）‎ ‎13．已知，则向量与向量的夹角是　　．‎ ‎【考点】数量积表示两个向量的夹角．‎ ‎【分析】据题意可得，∴ =进一步利用向量夹角的范围求出夹角．‎ ‎【解答】解：设的夹角为θ则 ‎∵‎ 即 ‎∵，‎ ‎∴‎ ‎∴=‎ ‎∵θ∈[0，π]‎ ‎∴‎ 故答案为：‎ ‎　‎ ‎14．若△ABC的内角A，B，C的对边分别为a，b，c，且a，b，c成等比数列，c=2a，则cosB的值为　　．‎ ‎【考点】余弦定理．‎ ‎【分析】由a，b，c，且a，b，c成等比数列且c=2a可得，b=，c=2a，结合余弦定理可求 ‎【解答】解：∵a，b，c，且a，b，c成等比数列且c=2a b2=ac=2a2，‎ b=，c=2a ‎=‎ 故答案为：‎ ‎　‎ ‎15．已知三棱柱ABC﹣A1B1C1的6个顶点都在球O的球面上，若AB=3cm，AC=4cm，AB⊥AC，AA1=12cm，则球O的表面积为　169π　cm2．‎ ‎【考点】球的体积和表面积；球内接多面体．‎ ‎【分析】由于直三棱柱ABC﹣A1B1C1的底面ABC为直角三角形，我们可以把直三棱柱ABC﹣A1B1C1补成四棱柱，则四棱柱的体对角线是其外接球的直径，求出外接球的直径后，代入外接球的表面积公式，即可求出该三棱柱的外接球的表面积．‎ ‎【解答】解：由题意，三棱柱ABC﹣A1B1C1为直三棱柱ABC﹣A1B1C1，底面ABC为直角三角形，把直三棱柱ABC﹣A1B1C1补成四棱柱，‎ 则四棱柱的体对角线是其外接球的直径，‎ 所以外接球半径为=13，‎ 则三棱柱ABC﹣A1B1C1外接球的表面积是4πR2=169πcm2．‎ 故答案为：169π．‎ ‎　‎ ‎16．如图（1）有面积关系=，则图（2）有体积关系=　　．‎ ‎【考点】类比推理．‎ ‎【分析】这是一个类比推理的题，在由平面图形到空间图形的类比推理中，一般是由点的性质类比推理到线的性质，由线的性质类比推理到面的性质，由面积的性质类比推理到体积性质．‎ ‎【解答】解：∵在由平面图形到空间图形的类比推理中，‎ 一般是由点的性质类比推理到线的性质，‎ 由线的性质类比推理到面的性质，‎ 由面积的性质类比推理到体积性质．‎ 故由（面积的性质）‎ 结合图（2）可类比推理出：‎ 体积关系： =‎ 故答案为：‎ ‎　‎ 三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）‎ ‎17．如图，四棱锥P﹣ABCD的底面ABCD是正方形，棱PD⊥底面ABCD，PD=DC，E是PC的中点．‎ ‎（1）证明：PA∥平面BDE；‎ ‎（2）证明：平面BDE⊥平面PBC．‎ ‎【考点】平面与平面垂直的判定；直线与平面平行的判定．‎ ‎【分析】（1）连结AC，设AC与BD交于O点，连结EO，易证EO为△PAC的中位线，从而OE∥PA，再利用线面平行的判断定理即可证得PA∥平面BDE；‎ ‎（2）依题意，易证DE⊥底面PBC，再利用面面垂直的判断定理即可证得平面BDE⊥平面PBC．‎ ‎【解答】证明：（1）连结AC，设AC与BD交于O点，连结EO．‎ ‎∵底面ABCD是正方形，‎ ‎∴O为AC的中点，又E为PC的中点，‎ ‎∴OE∥PA，‎ ‎∵OE⊂平面BDE，PA⊄平面BDE，‎ ‎∴PA∥平面BDE．…‎ ‎（2）∵PD=DC，E是PC的中点，‎ ‎∴DE⊥PC．‎ ‎∵PD⊥底面ABCD，‎ ‎∴PD⊥AD．又由于AD⊥CD，PD∩CD=D，故AD⊥底面PCD，‎ 所以有AD⊥DE．又由题意得AD∥BC，故BC⊥DE．‎ 于是，由BC∩PC=C，DE⊥PC，BC⊥DE可得DE⊥底面PBC．‎ 故可得平面BDE⊥平面PBC．…‎ ‎　‎ ‎18．已知f（x）=‎ ‎（Ⅰ）求函数f（x）的单调递增区间；‎ ‎（Ⅱ）在△ABC中，a，b，c分别是角A，B，C的对边，a=1且f（A）=3，求△ABC的面积S的最大值．‎ ‎【考点】二倍角的余弦；三角形的面积公式；正弦函数的单调性．‎ ‎【分析】（I）利用二倍角公式，化简函数为一个角的一个三角函数的形式，然后直接求出单调增区间；‎ ‎（II）首先根据f（A）=3求出∠A，然后由余弦定理a2=b2+c2﹣2bccosA及b2+c2≥2bc得出，进而可以求出三角形面积的最大值．‎ ‎【解答】解：（Ⅰ）∵f（x）==，…‎ ‎∴，‎ 解得．‎ ‎∴f（x）的单调递增区间为 ‎（Ⅱ）∵f（A）=3，∴．‎ ‎∵0＜A＜π，∴，即．‎ 又a2=b2+c2﹣2bccosA及 b2+c2≥2bc，∴，‎ ‎∴，当且仅当b=c时，取“=”．‎ ‎∴S的最大值为 ‎　‎ ‎19．已知一个几何体的三视图如图所示．‎ ‎（1）求此几何体的表面积；‎ ‎（2）如果点P，Q在正视图中所示位置：P为所在线段中点，Q为顶点，求在几何体表面上，从P点到Q点的最短路径的长．‎ ‎【考点】多面体和旋转体表面上的最短距离问题；由三视图求面积、体积．‎ ‎【分析】（1）由三视图知：此几何体是一个圆锥和一个圆柱的组合体，底面圆半径长a，圆柱高为2a，圆锥高为a．‎ ‎（2）将圆柱侧面展开，在平面矩形内线段PQ长为所求．‎ ‎【解答】解：（1）由三视图知：此几何体是一个圆锥加一个圆柱，其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和．底面圆半径长a，圆柱高为2a，圆锥高为a．﹣﹣﹣﹣﹣﹣﹣‎ ‎，﹣﹣﹣﹣﹣﹣﹣‎ ‎，﹣﹣﹣﹣﹣﹣‎ ‎，﹣﹣﹣﹣﹣﹣﹣‎ 所以．﹣﹣﹣﹣﹣﹣‎ ‎（2）沿P点与Q点所在母线剪开圆柱侧面，如上图．﹣﹣﹣﹣﹣﹣﹣‎ 则，﹣﹣﹣﹣﹣﹣‎ 所以从P点到Q点在侧面上的最短路径的长为．﹣﹣﹣﹣﹣﹣‎ ‎　‎ ‎20．已知以点C为圆心的圆经过点A（0，1）和B（4，3），且圆心在直线3x+y﹣15=0上．‎ ‎（Ⅰ）求圆C的方程；‎ ‎（Ⅱ）设点P在圆C上，求△PAB的面积的最大值．‎ ‎【考点】直线与圆的位置关系．‎ ‎【分析】（Ⅰ）设出圆的一般方程，利用待定系数法求圆C的方程；‎ ‎（Ⅱ）求出|AB|，P到AB距离的最大值为d+r，即可求△PAB的面积的最大值 ‎【解答】解：（Ⅰ）设所求圆的方程为x2+y2+Dx+Ey+F=0，‎ 依题意得；，‎ 解得：，‎ ‎∴所求圆的方程是x2+y2﹣12x+6y+5=0，‎ ‎（Ⅱ）∵|AB|==4，‎ 由已知知直线AB的方程为x﹣y﹣1=0，‎ 所以圆心C（6，﹣3）到AB的距离为d=4，…‎ P到AB距离的最大值为d+r=4+2，…‎ 所以△PAB面积的最大值为××（4+2）=…‎ ‎　‎ ‎21．如图AB是圆O的直径，点C是弧AB上一点，VC垂直圆O所在平面，D，E分别为VA，VC的中点．‎ ‎（1）求证：DE⊥VB；‎ ‎（2）若VC=CA=6，圆O的半径为5，求点E到平面BCD的距离．‎ ‎【考点】点、线、面间的距离计算；直线与平面垂直的判定．‎ ‎【分析】（1）利用直径对直角，得出AC⊥BC，再由直线VC⊥AC，证明AC⊥平面VBC，再由ED∥AC，得出ED⊥平面VBC，从而证明VB⊥DE；‎ ‎（2）利用等体积法，得到VE﹣BC=VB﹣CDE，即可求出点点到平面BCD的距离．‎ ‎【解答】证明：（1）∵AB是⊙O的直径，点C是⊙O上的点，‎ ‎∴AC⊥BC，‎ 又直线VC垂直于⊙O所在的平面，‎ ‎∴VC⊥AC，‎ 又VC∩BC=C，∴AC⊥平面VBC；‎ 又D、E分别是VA、VC的中点，‎ ‎∴ED∥AC，‎ ‎∴ED⊥平面VBC，‎ 又VB⊂平面VBC，‎ ‎∴VB⊥DE ‎（2）设点E到平面BCD 的距离为d，‎ 由VE﹣BC=VB﹣CDE得d•S△BCD=×8××3×3=12‎ ‎∵S△BCD=×8×3=12‎ 解得d=‎ 即点E到平面BCD的距离为．‎ ‎　‎ ‎22．设数列{an}的各项均为正数，它的前n项的和为Sn，点（an，Sn）在函数y=x2+x+的图象上；数列{bn}满足b1=a1，bn+1（an+1﹣an）=bn．其中n∈N*．‎ ‎（Ⅰ）求数列{an}和{bn}的通项公式；‎ ‎（Ⅱ）设cn=，求证：数列{cn}的前n项的和Tn＞（n∈N*）．‎ ‎【考点】数列的求和．‎ ‎【分析】（Ⅰ）根据数列项和前n项和之间的关系即可求数列{an}和{bn}的通项公式；‎ ‎（Ⅱ）求出cn=是表达式，利用错位相减法求出数列{cn}的前n项的和，即可得到结论．‎ ‎【解答】解：（1）∵点（an，Sn）在函数y=x2+x+的图象上，‎ ‎∴，①‎ 当n≥2时，，②‎ ‎①﹣②得：，‎ 即，‎ ‎∵数列{an}的各项均为正数，‎ ‎∴an﹣an﹣1=4（n≥2），‎ 又a1=2，∴an=4n﹣2；‎ ‎∵b1=a1，bn+1（an+1﹣an）=bn，‎ ‎∴，∴；‎ ‎（2）∵，‎ ‎∴，‎ ‎4Tn=4+3•42+5•43+…+（2n﹣3）•4n﹣1+（2n﹣1）•4n，‎ 两式相减得，‎ ‎∴．‎ ‎　‎