- 2021-06-24 发布 |
- 37.5 KB |
- 14页


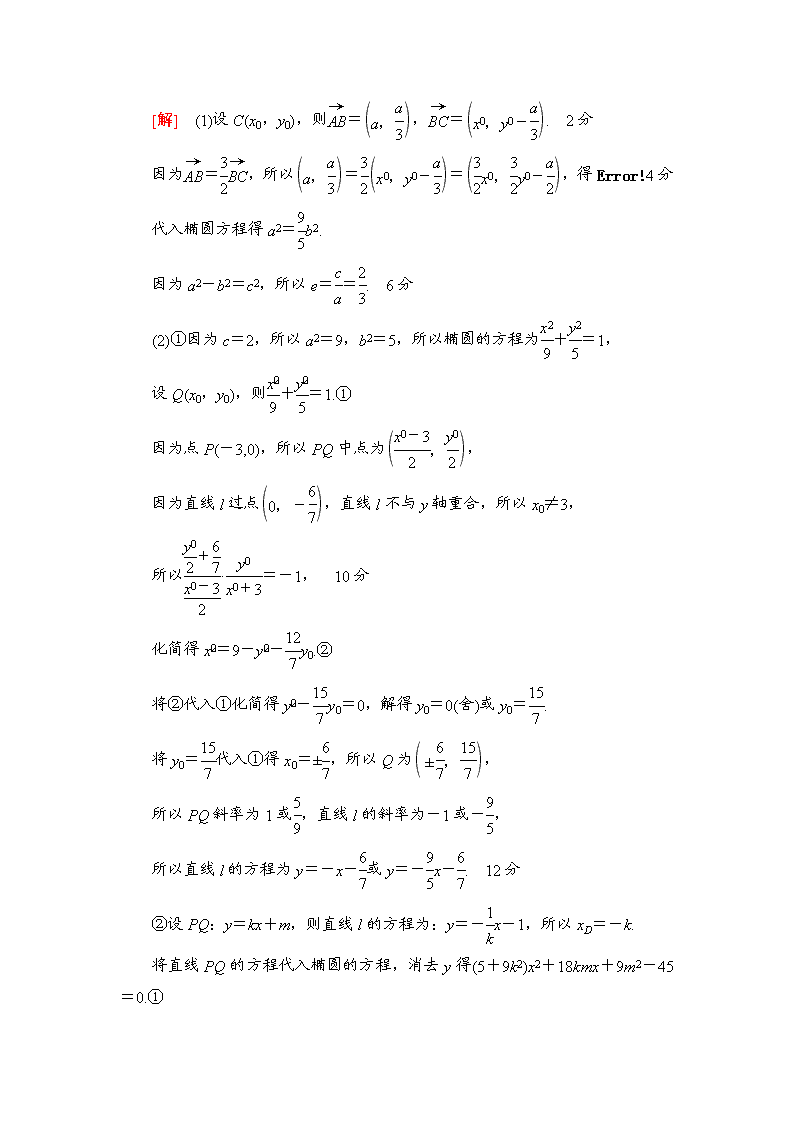
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017年高考数学(理科,江苏专版)二轮专题复习与策略(教师用书) 第1部分 专题5 第18讲 高考中的圆锥曲线
第18讲 高考中的圆锥曲线 题型一| 圆锥曲线中的最值(范围)问题 已知点A(0,-2),椭圆E:+=1(a>b>0)的离心率为,F是椭圆E的右焦点,直线AF的斜率为,O为坐标原点. (1)求E的方程; (2)设过点A的动直线l与E相交于P,Q两点,当△OPQ的面积最大时,求l的方程. [解] (1)设F(c,0),由条件知,=,得c=. 又=,所以a=2,b2=a2-c2=1. 故E的方程为+y2=1. 4分 (2)当l⊥x轴时不合题意, 故设l:y=kx-2,P(x1,y1),Q(x2,y2), 将y=kx-2代入+y2=1得 (1+4k2)x2-16kx+12=0. 6分 当Δ=16(4k2-3)>0,即k2>时,x1,2=. 从而|PQ|=|x1-x2|=. 8分 又点O到直线PQ的距离d=, 所以△OPQ的面积S△OPQ=d|PQ|=. 10分 设=t, 则t>0,S△OPQ==. 因为t+≥4,当且仅当t=2,即k=±时等号成立,且满足Δ>0, 14分 所以,当△OPQ的面积最大时l的方程为y=x-2或y=-x-2. 16分 【名师点评】 与圆锥曲线有关的最值的两种解法 1.数形结合法:根据待求值的几何意义,充分利用平面图形的几何性质求解. 2.构建函数法:先引入变量,构建以待求量为因变量的函数,再求其最值,常用均值不等式或导数法求最值(注意:有时需先换元后再求最值). (2016·南京盐城二模)在平面直角坐标系xOy中,点C在椭圆M:+=1(a>b>0)上.若点A(-a,0),B,且=. (1)求椭圆M的离心率; (2)设椭圆M的焦距为4,P,Q是椭圆M上不同的两点,线段PQ的垂直平分线为直线l,且直线l不与y轴重合. ①若点P(-3,0),直线l过点,求直线l的方程; ②若直线l过点(0,-1),且与x轴的交点为D,求D点横坐标的取值范围. [解] (1)设C(x0,y0),则=,=. 2分 因为=,所以==,得4分 代入椭圆方程得a2=b2. 因为a2-b2=c2,所以e==. 6分 (2)①因为c=2,所以a2=9,b2=5,所以椭圆的方程为+=1, 设Q(x0,y0),则+=1.① 因为点P(-3,0),所以PQ中点为, 因为直线l过点,直线l不与y轴重合,所以x0≠3, 所以·=-1, 10分 化简得x=9-y-y0.② 将②代入①化简得y-y0=0,解得y0=0(舍)或y0=. 将y0=代入①得x0=±,所以Q为, 所以PQ斜率为1或,直线l的斜率为-1或-, 所以直线l的方程为y=-x-或y=-x-. 12分 ②设PQ:y=kx+m,则直线l的方程为:y=-x-1,所以xD=-k. 将直线PQ的方程代入椭圆的方程,消去y得(5+9k2)x2+18kmx+9m2-45=0.① 设P(x1,y1),Q(x2,y2),中点为N, xN==-,代入直线PQ的方程得yN=, 代入直线l的方程得9k2=4m-5.② 又因为Δ=(18km)2-4(5+9k2)(9m2-45)>0, 化得m2-9k2-5<0. 14分 将②代入上式得m2-4m<0,解得0<m<4, 所以-<k<,且k≠0,所以xD=-k∈∪. 综上所述,点D横坐标的取值范围为∪. 16分 题型二| 圆锥曲线中的定点问题 如图18-1所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P是线段AM的垂直平分线与直线CM的交点. (1)求点P的轨迹曲线E的方程; (2)设点P(x0,y0)是曲线E上任意一点,写出曲线E在点P(x0,y0)处的切线l的方程;(不要求证明) (3)直线m过切点P(x0,y0)与直线l垂直,点C关于直线m的对称点为D,证明:直线PD恒过一定点,并求定点的坐标. 图18-1 [解] (1)∵点P是线段AM的垂直平分线与直线CM的交点, ∴PA=PM, PA+PC=PM+PC=2>AC=2, ∴动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆. 3分 椭圆的长轴长为2a=2,焦距2c=2. ∴a=,c=1,b2=1. ∴曲线E的方程为+y2=1. 5分 (2)曲线E在点P(x0,y0)处的切线l的方程是+y0y=1. 7分 (3)证明:直线m的方程为x0(y-y0)=2y0(x-x0),即2y0x-x0y-x0y0=0. 设点C关于直线m的对称点的坐标为D(m,n), 则 解得 10分 ∴直线PD的斜率为k==, 12分 从而直线PD的方程为 y-y0=(x-x0), 14分 即x=y+1,从而直线PD恒过定点A(1,0). 16分 【名师点评】 1.动直线l过定点问题解法:设动直线方程(斜率存在)为y=kx+t,由题设条件将t用k表示为t=mk,得y=k(x+m),故动直线过定点(-m,0). 2.动曲线C过定点问题解法:引入参变量建立曲线C的方程,再根据其对参变量恒成立,令其系数等于零,得出定点. (2016·苏北四市期末)如图18-2,在平面直角坐标系xOy中,已知椭圆C:+=1(a>b>0)的离心率e=,左顶点为A(-4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E. 图18-2 (1)求椭圆C的方程; (2)已知点P为AD的中点,是否存在定点Q,对于任意的k(k≠0)都有OP⊥EQ?若存在,求出点Q的坐标;若不存在,说明理由; (3)若过点O作直线l的平行线交椭圆C于点M,求的最小值. [解] (1)因为左顶点为A(-4,0),所以a=4,2分 又e=,所以c=2,b2=a2-c2=12, 所以椭圆C的标准方程为+=1. 5分 (2)直线l的方程为y=k(x+4),由消元得,+=1. 化简得(x+4)[(4k2+3)x+16k2-12]=0,所以x1=-4,x2=. 10分 当x=时,y=k=,所以D. 因为P为AB的中点, 所以P的坐标为,kOP=-(k≠0), 直线l的方程为y=k(x+4),令x=0得E点坐标为(0,4k), 假设存在定点Q(m,n)(m≠0),使得OP⊥EQ,则kOPkEQ=-1,即-·=-1恒成立, 所以(4m+12)k-3n=0恒成立,所以即 所以定点Q的坐标为(-3,0). 12分 (3)因为OM∥l,所以OM的方程可设为y=kx, 由得M点的横坐标为x=±, 由OM∥l,得== ==· =≥2, 当且仅当=即k=±时取等号, 所以当k=±时,的最小值为2. 16分 题型三| 圆锥曲线中的定值问题 (2016·苏锡常镇调研一)在平面直角坐标系xOy中,已知椭圆C:+=1(a>b>0)过点P,离心率为. (1)求椭圆C的方程; (2)设直线l与椭圆C交于A,B两点. ①若直线l过椭圆C的右焦点,记△ABP三条边所在直线的斜率的乘积为t,求t的最大值; ②若直线l的斜率为,试探究OA2+OB2是否为定值?若是定值,则求出此定值;若不是定值,请说明理由. [解] (1)+=1,=,得a2=4,b2=3. 2分 所以椭圆C:+=1. 3分 (2)①设直线l的方程为x=my+1,直线l与椭圆C的交点为A(x1,y1),B(x2,y2), 由化简得(3m2+4)y2+6my-9=0,易知Δ>0, 5分 所以y1+y2=-,y1y2=-, 所以kAP·kBP=·=·=· =--, 7分 所以t=kAB·kAP·kBP=--=-2+, 9分 所以当m=-时,t有最大值. 10分 ②设直线l的方程为y=x+n,直线l与椭圆C的交点为A(x1,y1),B(x2,y2),得3x2+2nx+2n2-6=0, Δ=(2n)2-4×3(2n2-6)>0,即-查看更多