2018-2019学年安徽省宣城市高二下学期期末考试数学（理）试题 Word版

2018-2019学年安徽省宣城市高二下学期期末考试数学（理）试题 Word版

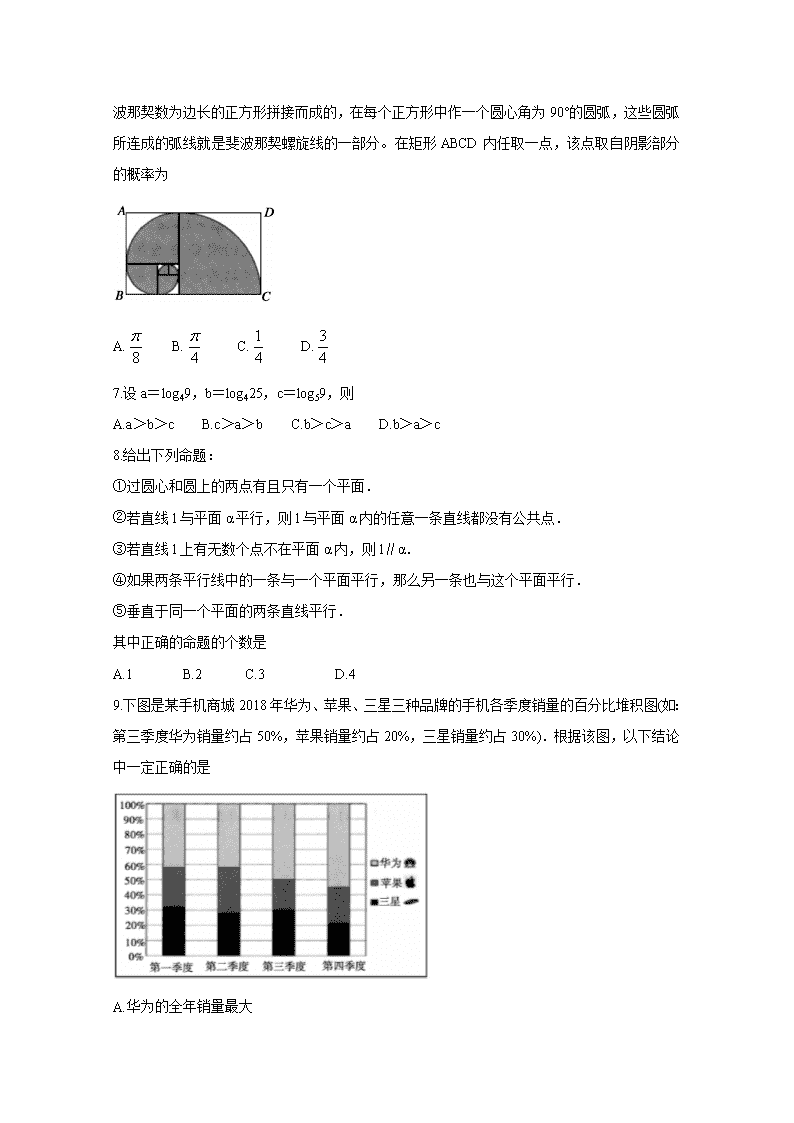
宣城市2018—2019学年度第二学期期末调研测试 高二数学试题(理科)‎ 考生注意事项：‎ ‎1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，满分150分，考试时间120分钟。‎ ‎2.答题前，考生先将自己的姓名、考号在答题卷指定位置填写清楚并将条形码粘贴在指定区域。‎ ‎3.考生作答时，请将答案答在答题卷上.第Ⅰ卷每小题选出答案后，用2B铅笔把答题卷上对应题目的答案标号涂黑；第Ⅱ卷请用0.5毫米的黑色墨水签字笔在答题卷上各题的答题区域内作答，超出答题区域书写的答案无效，在试题卷、草稿纸上作答无效。‎ ‎4.考试结束时，务必将答题卡交回。‎ 第Ⅰ卷(选择题 共60分)‎ 一、选择题：本大题共12小题，每小题5分，共60分。在每小题四个选项中，只有一项是符合要求的。‎ ‎1.设，则A∩B＝‎ A. B.(1，3］ C.(－∞，) D.(，3］‎ ‎2.设i为虚数单位，复数z满足(1－i)·z＝2i，则︱z︱＝‎ A.1 B. C. D.2‎ ‎3.设等差数列｛an｝的前n项和为Sn，若a1＋a3＋a5＝15，S4＝16，则a4＝‎ A.9 B.8 C.7 D.6‎ ‎4.已知变量x，y满足约束条件，则目标函数z＝x＋2y的最大值为 A.7 B.8 C.9 D.10‎ ‎5.将函数的图像向左平移个单位长度后，所得图像的一个对称中心为 A. B. C. D.‎ ‎6.斐波那契螺旋线，也称“黄金螺旋线”，是根据斐波那契数列(1，1，2，3，5，8……)画出来的螺旋曲线，由中世纪意大利数学家列奥纳多·斐波那契最先提出。如图，矩形ABCD 是以斐波那契数为边长的正方形拼接而成的，在每个正方形中作一个圆心角为90°的圆弧，这些圆弧所连成的弧线就是斐波那契螺旋线的一部分。在矩形ABCD内任取一点，该点取自阴影部分的概率为 A. B. C. D.‎ ‎7.设a＝log49，b＝log425，c＝log59，则 A.a＞b＞c B.c＞a＞b C.b＞c＞a D.b＞a＞c ‎8.给出下列命题：‎ ‎①过圆心和圆上的两点有且只有一个平面．‎ ‎②若直线l与平面α平行，则l与平面α内的任意一条直线都没有公共点．‎ ‎③若直线l上有无数个点不在平面α内，则l∥α．‎ ‎④如果两条平行线中的一条与一个平面平行，那么另一条也与这个平面平行．‎ ‎⑤垂直于同一个平面的两条直线平行．‎ 其中正确的命题的个数是 A.1 B.2 C.3 D.4‎ ‎9.下图是某手机商城2018年华为、苹果、三星三种品牌的手机各季度销量的百分比堆积图(如：第三季度华为销量约占50%，苹果销量约占20%，三星销量约占30%)．根据该图，以下结论中一定正确的是 A.华为的全年销量最大 B.苹果第二季度的销量大于第三季度的销量 C.华为销量最大的是第四季度 D.三星销量最小的是第四季度 ‎10.函数，的大致图像为 ‎11.已知O为坐标原点，双曲线C：的右焦点为F，焦距为，C的一条渐近线被以F为圆心，OF为半径的圆F所截得的弦长为2，则C的方程是 ‎ ‎ ‎12.已知函数，若方程有五个不同的实数根，则a的取值范围是 A.(0，＋∞) B.(0，1) C.(－∞，0) D. ‎ 二、填空题：本大题共4小题，每小题5分，共20分。把答案填在题中的横线上。‎ ‎13.已知平面向量a，b满足︱a︱＝2，︱b︱＝3，a－b＝()，︱a＋b︱＝ ‎ ‎14.执行如图所示的程序框图，则输出的i的值为 ‎ ‎15.已知抛物线E：y2＝x的焦点为F，准线为l，过F的直线M与E交于A，B两点，过A作AM⊥l，垂足为M，AM的中点为N，若AM⊥FN，则︱AB︱＝ ‎ ‎16.在三棱锥P－ABC中，AB＝BC＝1，AC＝PA＝PC＝，PB＝，记三棱锥P－ABC的体积为V1，其外接球的体积为V2，则＝ ‎ 三、解答题：本大题共6小题，满分70分。解答应写出必要的文字说明、证明过程和演算步骤。‎ ‎17.(本题满分10分)‎ 设数列｛an｝的前n项和为Sn。已知a1＝0，Sn＋1＝Sn＋an＋2n－2。‎ ‎(1)若bn＝2n－an，证明：数列｛bn｝是等差数列；‎ ‎(2)求｛an｝的前n项和Sn．‎ ‎18.(本题满分12分)‎ 在△ABC中，角A，B，C所对的边分别为a，b，c，已知2b＋c＝2acosC．‎ ‎(1)求角A；‎ ‎(2)若b＝3，a－c＝2，求△ABC的面积．‎ ‎19.(本题满分12分)‎ 如图，矩形ABCD中，AB＝2BC，以BD为折痕把△BDC折起，使点C到达点P的位置，且PA⊥PB．‎ ‎(1)证明：平面PAB⊥平面ABCD；‎ ‎(2)求AB与平面PBD所成角的正弦值．‎ ‎20.(本题满分12分)‎ 在平面直角坐标系xOy中，已知椭圆C：的焦距为4，且过点(2，)。‎ ‎(1)求椭圆C的方程；‎ ‎(2)设椭圆C的上顶点为B，右焦点为F，直线l与椭圆交于M、N两点，问是否存在直线l，使得F为△BMN的垂心。若存在，求出直线l的方程；若不存在，说明理由。‎ ‎21.(本题满分12分)‎ 设函数，曲线y＝f(x)在点(1，f(1))处的切线与y轴垂直。‎ ‎(1)求b的值；‎ ‎(2)若存在x0≥1，使得，求a的取值范围。‎ ‎22.(本题满分12分)‎ 十九大以来，某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求，带领广大农村地区人民群众脱贫奔小康．经过不懈的奋力拼搏，新农村建设取得巨大进步，农民年收入也逐年增加。为了更好的制定2019年关于加快提升农民年收入力争早日脱贫的工作计划，该地扶贫办统计了2018年50位农民的年收人并制成如下频率分布直方图：‎ ‎(1)根据频率分布直方图，估计50位农民的年平均收入 (单位：千元)(同一组数据用该组数据区间的中点值表示)；‎ ‎(2)由频率分布直方图，可以认为该贫困地区农民年收入X服从正态分布N(μ，σ2)，其中μ近似为年平均收入近似为样本方差s2，经计算得s2＝6.92．利用该正态分布，求：‎ ‎(i)在2019年脱贫攻坚工作中，若使该地区约有占总农民人数的84.14%的农民的年收入高于扶贫办制定的最低年收入标准，则最低年收入大约为多少千元？‎ ‎(ii)为了调研“精准扶贫，不落一人”的政策要求落实情况，扶贫办随机走访了1000位农民。若每个农民的年收人相互独立，问：这1000位农民中的年收入不少于12.14千元的人数最有可能是多少？‎ 附：参考数据与公式，若X～N(μ，σ2)，则 ‎①；‎ ‎②；‎ ‎③。‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎