高三数学二轮高考专题辅导与训练打包检测试题：专题六第2讲课时训练提能

高三数学二轮高考专题辅导与训练打包检测试题：专题六第2讲课时训练提能

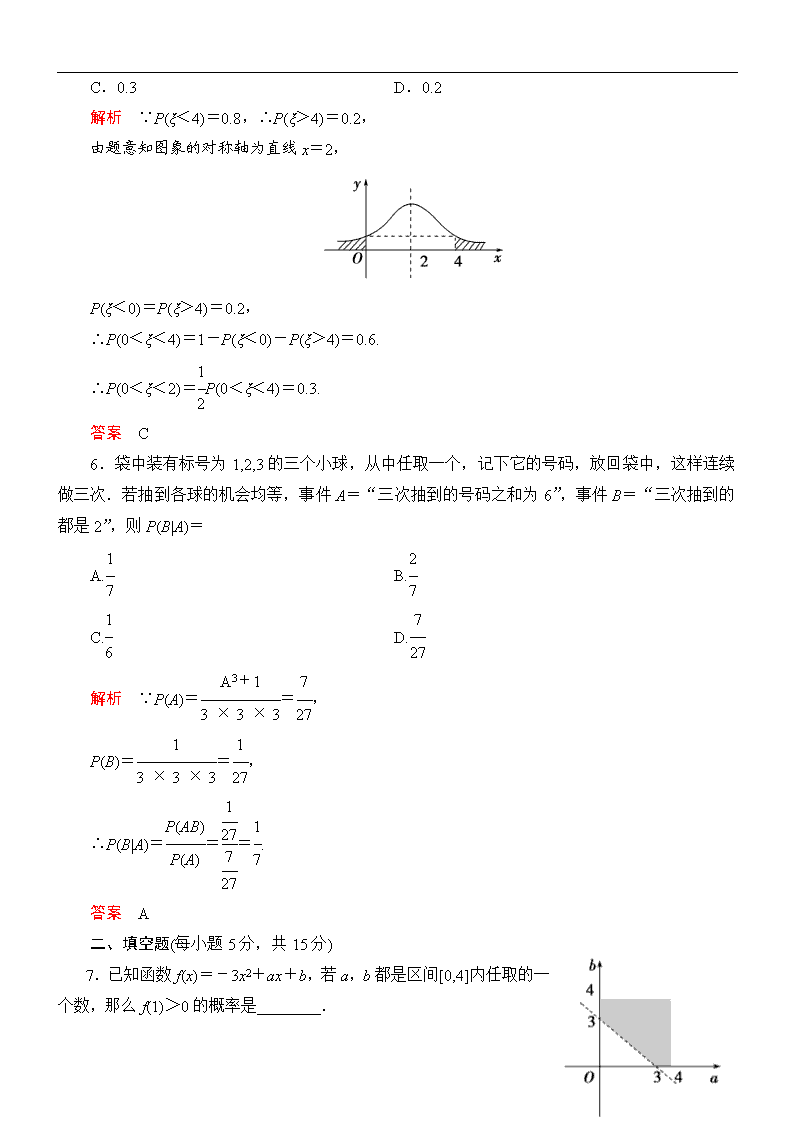
专题六 第2讲　概率、随机变量及其分布列 课时训练提能 ‎[限时45分钟，满分75分]‎ 一、选择题(每小题4分，共24分)‎ ‎1．(2012·威海模拟)甲、乙两人进行跳绳比赛，规定：若甲赢一局，比赛结束，甲胜出；若乙赢两局，比赛结束，乙胜出．已知每一局甲、乙二人获胜的概率分别为、，则甲胜出的概率为 A.　 　 　 B. C.　 　 　 D. 解析　若甲赢第一局，则P1＝；‎ 若甲第一局输，第二局赢，‎ 则P2＝×＝，‎ 则甲胜出的概率为P＝P1＋P2＝＋＝.‎ 答案　A ‎2．一个袋中装有2个红球和2个白球，现从袋中取出1个球，然后放回袋中再取出1个球，则取出的2个球同色的概率为 A. B. C. D. 解析　把红球标记为红1、红2，白球标记为白1、白2，本试验的基本事件共有16个，其中2个球同色的事件有8个：红1、红1，红1、红2，红2、红1、红2、红2，白1、白1，白1、白2，白2、白1，白2、白2，故所求概率为P＝＝.‎ 答案　A ‎3．(2012·西城二模)已知函数f(x)＝kx＋1，其中实数k随机选自区间[－2,1]．对∀x∈[0,1]，f(x)≥0的概率是 A. B. C. D. 解析　当x＝0时，f(x)＝kx＋1≥0对任意的k∈R恒成立，‎ 当x∈(0,1]时，要使f(x)＝kx＋1≥0，需k≥－，‎ 而－∈(－∞，－1]，∴k≥－1，即k∈[－1,1]，‎ 故所求的概率为P＝＝.‎ 答案　C ‎4．甲、乙两人各自独立加工1个零件，他们把零件加工为合格品的概率分别为和，则这两个零件中恰有1个合格品的概率为 A. B. C. D. 解析　“两个零件中恰有1个合格品”有两种可能性：“甲加工的零件合格且乙加工的零件不合格”，“乙加工的零件合格且甲加工的零件不合格”．根据独立事件同时发生的概率公式和互斥事件有一个发生的概率公式可得所求概率为P＝×＋×＝.‎ 答案　B ‎5．已知随机变量ξ服从正态分布N(2，σ2)，且P(ξ＜4)＝0.8，则P(0＜ξ＜2)＝‎ A．0.6 B．0.4‎ C．0.3 D．0.2‎ 解析　∵P(ξ＜4)＝0.8，∴P(ξ＞4)＝0.2，‎ 由题意知图象的对称轴为直线x＝2，‎ P(ξ＜0)＝P(ξ＞4)＝0.2，‎ ‎∴P(0＜ξ＜4)＝1－P(ξ＜0)－P(ξ＞4)＝0.6.‎ ‎∴P(0＜ξ＜2)＝P(0＜ξ＜4)＝0.3.‎ 答案　C ‎6．袋中装有标号为1,2,3的三个小球，从中任取一个，记下它的号码，放回袋中，这样连续做三次．若抽到各球的机会均等，事件A＝“三次抽到的号码之和为‎6”‎，事件B＝“三次抽到的都是‎2”‎，则P(B|A)＝‎ A. B. C. D. 解析　∵P(A)＝＝，‎ P(B)＝＝，‎ ‎∴P(B|A)＝＝＝.‎ 答案　A 二、填空题(每小题5分，共15分)‎ ‎7．已知函数f(x)＝－3x2＋ax＋b，若a，b都是区间[0,4]内任取的一个数，那么f(1)＞0的概率是________．‎ 解析　由f(1)＞0得－3＋a＋b＞0，‎ 即a＋b＞3.‎ 在0≤a≤4,0≤b≤4的约束条件下，作出a＋b＞3满足的可行域，如图，则根据几何概型概率公式可得，f(1)＞0的概率P＝＝‎ eq f(23,32).‎ 答案　 ‎8．将4个不同的小球任意放入3个不同的盒子中，则每个盒子中至少有1个小球的概率为________．‎ 解析　将4个不同的小球任意放入3个不同的盒子中，每个小球有3种不同的放法，共有34＝81种放法，每个盒子中至少有1个小球的放法有CCA＝36种，故所求的概率P＝＝.‎ 答案　 ‎9．(2012·梅州模拟)如果在一次试验中，某事件A发生的概率为p，那么在n次独立重复试验中，事件A发生偶数次的概率为________．‎ 解析　设事件A发生偶数次的概率为X，则事件A发生奇数次的概率为1－X，‎ ‎∴X＝Cp0(1－p)n＋Cp2(1－p)n－2＋Cp4(1－p)n－4＋…，‎ ‎1－X＝Cp(1－p)n－1＋Cp3(1－p)n－3＋Cp5(1－p)n－5＋…，‎ 两式相减，得2X－1＝Cp0(1－p)n－Cp(1－p)n－1＋Cp2(1－p)n－2－…‎ ‎＝[(1－p)－p]n＝(1－2p)n，‎ ‎∴X＝[1＋(1－2p)n]．‎ 答案　[1＋(1－2p)n]‎ 三、解答题(每小题12分，共36分)‎ ‎10．已知集合A＝{xx2＋3x－4＜0}，B＝.‎ ‎(1)在区间(－4,5)上任取一个实数x，求“x∈A∩B”的概率；‎ ‎(2)设(a，b)为有序实数对，其中a，b分别是集合A，B中任取的一个整数，求“a－b∈A∪B”的概率．‎ 解析　(1)由已知得A＝{xx2＋3x－4＜0}＝{x－4＜x＜1}，‎ B＝＝{x－2＜x＜4}，显然A∩B＝{x－2＜x＜1}．‎ 设事件“x∈A∩B”的概率为P1，由几何概型的概率公式得P1＝＝.‎ ‎(2)依题意，(a，b)的所有可能的结果一共有以下20种：‎ ‎(－3，－1)，(－3,0)，(－3,1)，(－3,2)，(－3,3)，(－2，－1)，(－2,0)，(－2,1)，(－2,2)，(－2,3)，(－1，－1)，(－1,0)，(－1,1)，(－1,2)，(－1,3)，(0，－1)，(0,0)，(0,1)，(0,2)，(0,3)．‎ 又A∪B＝{x－4＜x＜4}，因此“a－b∈A∪B”的所有可能的结果一共有以下14种：(－3，－1)，(－3,0)，(－2，－1)，(－2,0)，(－2,1)，(－1，－1)，(－1,0)，(－1,1)，(－1,2)，(0，－1)，(0,0)，(0,1)，(0,2)，(0,3)．‎ 所以“a－b∈A∪B”的概率P2＝＝.‎ ‎11．(2012·郴州模拟)一个袋子中装有大小形状完全相同的编号分别为1,2,3,4,5的5个红球与编号为1,2,3,4的4个白球，从中任意取出3个球．‎ ‎(1)求取出的3个球颜色相同且编号是三个连续整数的概率；‎ ‎(2)求取出的3个球中恰有2个球编号相同的概率；‎ ‎(3)设X为取出的3个球中编号的最大值，求X的分布列与数学期望．‎ 解析　(1)设“取出的3个球颜色相同且编号是三个连续整数”为事件A，则P(A)＝＝.‎ 即取出的3个球的编号恰好是3个连续的整数，且颜色相同的概率为.‎ ‎(2)设“取出的3个球中恰有两个球编号相同”为事件B，则 P(B)＝＝＝.‎ 即取出的3个球中恰有两个球编号相同的概率为.‎ ‎(3)X的取值为2,3,4,5.‎ P(X＝2)＝＝，P(X＝3)＝＝，‎ P(X＝4)＝＝，‎ P(X＝5)＝＝.‎ 所以X的分布列为 X ‎2‎ ‎3‎ ‎4‎ ‎5‎ P X的数学期望EX＝2×＋3×＋4×＋5×＝.‎ ‎12．(2012·大连模拟)某游乐场将要举行狙击移动靶比赛．比赛规则是：每位选手可以选择在A区射击3次或选择在B区射击2次，在A区每射中一次得3分，射不中得0分；在B区每射中一次得2分，射不中得0分．已知参赛选手甲在A区和B区每次射中移动靶的概率分别是和p(0＜p＜1)．‎ ‎(1)若选手甲在A区射击，求选手甲至少得3分的概率；‎ ‎(2)我们把在A、B两区射击得分的数学期望高者作为选择射击区的标准，如果选手甲最终选择了在B区射击，求p的取值范围．‎ 解析　(1)设“选手甲在A区射击得0分”为事件M，“选手甲在A区射击至少得3分”为事件N，则事件M与事件N为对立事件，‎ P(M)＝C·0·3＝，P(N)＝1－P(M)＝1－＝.‎ ‎(2)设选手甲在A区射击的得分为ξ，‎ 则ξ的可能取值为0,3,6,9.‎ P(ξ＝0)＝3＝；P(ξ＝3)＝C··2＝；‎ P(ξ＝6)＝C2＝；P(ξ＝9)＝3＝.‎ ‎∴ξ分布列为 ξ ‎0‎ ‎3‎ ‎6‎ ‎9‎ P ‎∴Eξ＝0×＋3×＋6×＋9×＝.‎ 设选手甲在B区射击的得分为η，‎ 则η的可能取值为0,2,4.‎ P(η＝0)＝(1－p)2；P(η＝2)＝C·p·(1－p)＝2p(1－p)；P(η＝4)＝p2，‎ 所以η的分布列为 η ‎0‎ ‎2‎ ‎4‎ P ‎(1－p)2‎ ‎2p(1－p)‎ p2‎ ‎∴Eη＝0×(1－p)2＋2·2p(1－p)＋4·p2＝4p，‎ 根据题意，有Eη＞Eξ，∴4p＞，∴＜p＜1.‎