2018-2019学年甘肃省天水市一中高一上学期暑假开学考试数学试题

2018-2019学年甘肃省天水市一中高一上学期暑假开学考试数学试题

‎2018-2019学年甘肃省天水市一中高一上学期暑假开学考试数学试题 ‎（满分：100分 时间：60分钟）‎ 一、选择题（每题4分，共40分）‎ ‎1．下列各式能用完全平方公式进行分解因式的是（ ）‎ A．x2+1 B．x2+2x﹣1 C．x2+x+1 D．x2+4x+4‎ ‎2．下列二次根式中的最简二次根式是 （ ）‎ A． B． C． D．‎ ‎3．如图，一次函数的图像与反比例函数的图像相交于A,B两点，则图中使反比例函数的值小于一次函数的值的x的取值范围是（ ）‎ A．x＜-1 B．x＜-1或0＜x＜2 ‎ C．x＞2 D．-1＜x＜0或x＞2‎ ‎4．下列各式正确的是( )‎ A. =a B. a0=1 ‎ C. =-4 D. =-5‎ ‎5．关于x的分式方程=1，下列说法正确的是（ ）‎ A．m＜-5时，方程的解为负数 B．方程的解是x=m+5‎ C．m＞-5时，方程的解是正数 D．无法确定 ‎6．不等式x＜x2的解集是（ ）‎ A．（﹣∞，0） B．（0，1） C．（1，+∞） D．（﹣∞，0）∪（1，+∞）‎ ‎7.多项式的一个因式为（ ）‎ A. B. C. D.‎ ‎8.已知不等式x2＋ax＋4<0的解集为空集，则a的取值范围是(　　)‎ A. －4≤a≤4 B. －44‎ ‎9．如图，若一次函数y＝ax＋b的图象经过二、三、四象限，则二次函数y＝ax2＋bx的图象可能是(　　)‎ A. B. C. D. ‎ ‎10.若实数，且满足，则代数式 的值为（ ）‎ A. B. C. D.‎ 二、填空题（每题4分，共16分）‎ ‎11．函数与的图象在同一平面直角坐标系内的交点的个数是_________． ‎ ‎12．分解因式：=_______ ．‎ ‎13．要使式子有意义，的取值范围是 ．‎ 第14题图 ‎14. 已知二次函数的图象如图所示，则下列6个代数式：、、、、、中，其值为正的式子的个数是______.‎ 三、解答题 ‎15．（10分）把下列各式分解因式 ‎（1） （2）‎ ‎16．（10分）已知一元二次函数.‎ ‎（1）试判断该函数的图象与x轴有没有交点，有几个交点？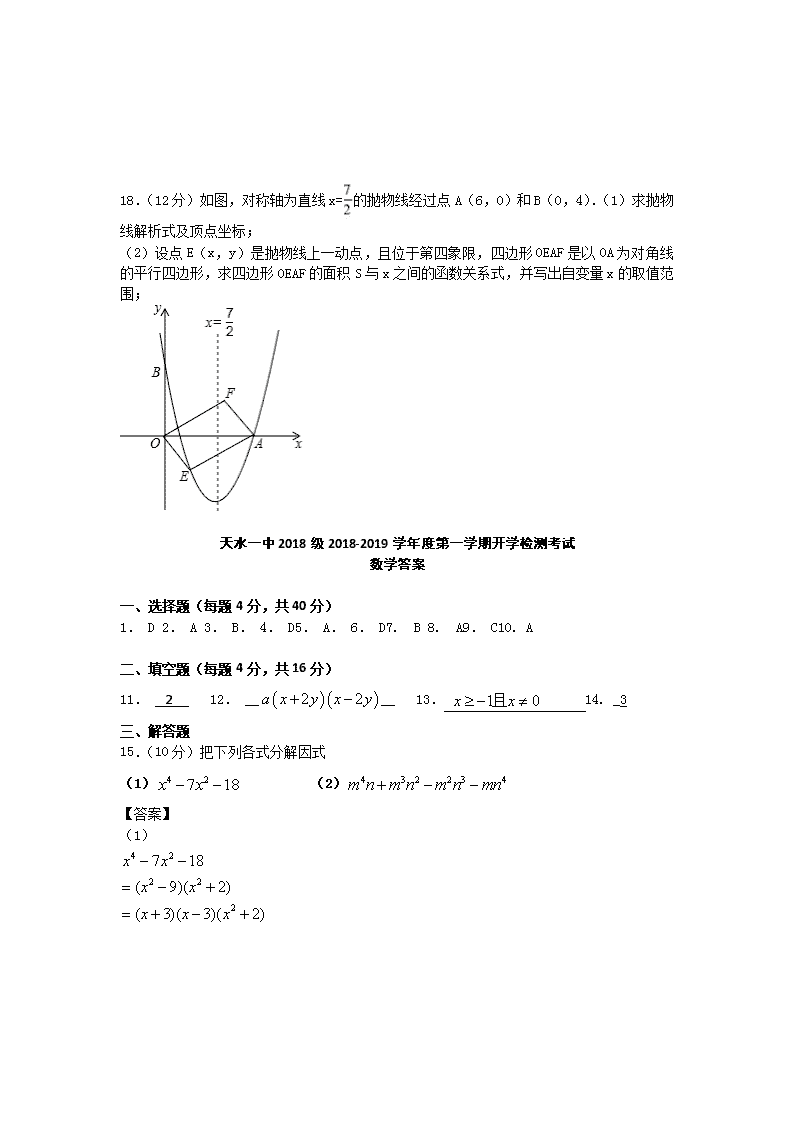‎ ‎（2）若该函数的图象与x轴有两个交点，试用m表示并求出它的最小值.‎ ‎17．（12分）若不等式kx2-2x+6k<0（k≠0）.‎ ‎（1）若不等式解集是{x|x<-3或x>-2}，求k的值；‎ ‎（2）若不等式解集是R，求k的取值.‎ ‎18．（12分）如图，对称轴为直线x=的抛物线经过点A（6，0）和B（0，4）．（1）求抛物线解析式及顶点坐标；‎ ‎（2）设点E（x，y）是抛物线上一动点，且位于第四象限，四边形OEAF是以OA为对角线的平行四边形，求四边形OEAF的面积S与x之间的函数关系式，并写出自变量x的取值范围；‎ 天水一中2018级2018-2019学年度第一学期开学检测考试 数学答案 一、选择题（每题4分，共40分）‎ ‎1． D 2． A 3． B． 4． D5． A． 6． D7. B 8. A9． C10. A 二、填空题（每题4分，共16分）‎ ‎11． _ 2 __ 12． ____ 13． 14. _3‎ 三、解答题 ‎15．（10分）把下列各式分解因式 ‎（1） （2）‎ ‎【答案】‎ ‎（1）‎ ‎（2）‎ ‎16．‎ ‎（10分）已知一元二次函数.‎ ‎（1）试判断该函数的图象与x轴有没有交点，有几个交点？‎ ‎（2）若该函数的图象与x轴有两个交点，试用m表示并求出它的最小值。‎ 解：（1）‎ 所以该函数的图象与x轴有有2个不同的交点。‎ ‎（2）由韦达定理 所以 即的最小值为3‎ ‎17．（12分）若不等式kx2-2x+6k<0（k≠0）.‎ ‎（1）若不等式解集是{x|x<-3或x>-2}，求k的值；‎ ‎（2）若不等式解集是R，求k的取值.‎ ‎【答案】(1) ；(2) ‎ ‎【解析】试题分析：（1）一元二次不等式的解集的端点值应该为其对应方程的根，所以可利用根与系数的关系解得参数；（2）一元二次不等式的恒成立问题，可以结合二次函数图像，得到不等式组，解之即可．‎ 试题解析：（1）∵不等式kx2－2x＋6k<0的解集为{x|x<－3或x>－2}，‎ ‎∴x1＝－3与x2＝－2是方程kx2－2x＋6k＝0（k≠0）的两根，‎ ‎∴－＝＝－3－2，∴k＝－；‎ ‎（2）若不等式的解集为R，即kx2－2x＋6k<0恒成立，‎ 则满足，∴k<－， ∴k∈{k|k<－}．‎ 考点：1．一元二次不等式的解法；2．一元二次不等式恒成立问题．‎ ‎18．（12分）如图，对称轴为直线x=的抛物线经过点A（6，0）和B（0，4）．（1）求抛物线解析式及顶点坐标；‎ ‎（2）设点E（x，y）是抛物线上一动点，且位于第四象限，四边形OEAF是以OA为对角线的平行四边形，求四边形OEAF的面积S与x之间的函数关系式，并写出自变量x的取值范围；‎ 正确答案 解：（1）由题可设抛物线的解析式为y=a（x-）2+k，‎ ‎∵抛物线经过点A（6，0）和B（0，4），‎ ‎∴．‎ 解得；．‎ ‎∴抛物线的解析式为y=（x-）2-，此时顶点坐标为（，-）．‎ ‎（2）过点E作EH⊥OA，垂足为H，如图1，‎ 由（x-）2-=0得x1=1，x2=6．‎ ‎∵点E（x，y）是抛物线上位于第四象限一动点，‎ ‎∴1＜x＜6，-≤y＜0．‎ ‎∵四边形OEAF是平行四边形，‎ ‎∴△OAE≌△AOF．‎ ‎∴S=2S△OAE=2×OA•EH=OA•EH ‎=-6y ‎=-6×[（x-）2-]‎ ‎=-4（x-）2+25．‎ ‎∴四边形OEAF的面积S与x之间的函数关系式为S=-4（x-）2+25，其中1＜x＜6． ‎