高中数学选修2-2课时提升作业(十四) 2_1_1

高中数学选修2-2课时提升作业(十四) 2_1_1

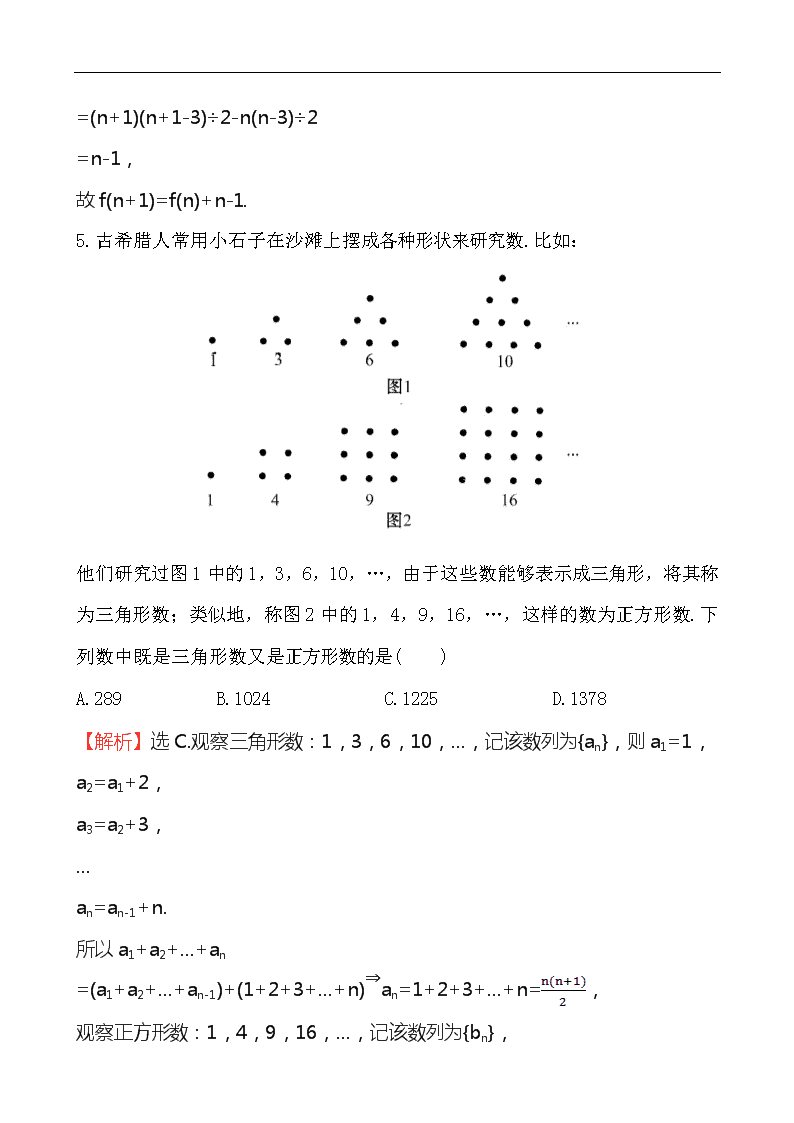
温馨提示：‎ ‎ 此套题为Word版，请按住Ctrl,滑动鼠标滚轴，调节合适的观看比例，答案解析附后。关闭Word文档返回原板块。‎ 课时提升作业(十四)‎ 合情推理 一、选择题(每小题3分，共18分)‎ ‎1.某同学在电脑上打下了一串黑白圆，如图所示，，按这种规律往下排，那么第36个圆的颜色应是(　　)‎ A.白色 B.黑色 C.白色可能性大 D.黑色可能性大 ‎【解析】选A.由题干图知，图形是三白二黑的圆周而复始相继排列，是一个周期为5的三白二黑的圆列，因为36÷5=7余1，所以第36个圆应与第1个圆颜色相同，即白色.‎ ‎2.已知数列{an}满足a0=1，an=a0+a1+a2+…+an-1(n≥1)，则当n≥1时，an等于(　　)‎ A.2n B.n(n+1)‎ C.2n-1 D.2n-1‎ ‎【解析】选C.a0=1，a1=a0=1，‎ a2=a0+a1=‎2a1=2，‎ a3=a0+a1+a2=‎2a2=4，‎ a4=a0+a1+a2+a3=‎2a3=8，…，‎ 猜想n≥1时，an=2n-1.‎ ‎3.给出下列三个类比结论：‎ ‎①类比ax·ay=ax+y，则有ax÷ay=ax-y；‎ ‎②类比loga(xy)=logax+logay，则有sin(α+β)=sinαsinβ；‎ ‎③类比(a+b)2=a2+2ab+b2，则有(a+b)2=a2+‎2a·b+b2.‎ 其中结论正确的个数是(　　)‎ A.0 B‎.1 ‎ C.2 D.3‎ ‎【解析】选C.根据指数的运算法则知ax÷ay=ax-y，故①正确；根据三角函数的运算法则知：sin(α+β)≠sinαsinβ，②不正确；根据向量的运算法则知：(a+b)2=a2+‎2a·b+b2，③正确.‎ ‎4.设n棱柱有f(n)个对角面，则(n+1)棱柱的对角面的个数f(n+1)等于(　　)‎ A.f(n)+n+1 B.f(n)+n C.f(n)+n-1 D.f(n)+n-2‎ ‎【解题指南】因为过不相邻两条侧棱的截面为对角面，过每一条侧棱与它不相邻的一条侧棱都能作对角面，可作(n-3)个对角面，n条侧棱可作n(n-3)个对角面，由于这些对角面是相互之间重复计算了，所以共有n(n-3)÷2个对角面，从而得出f(n+1)与f(n)的关系.‎ ‎【解析】选C.因为过不相邻两条侧棱的截面为对角面，过每一条侧棱与它不相邻的一条侧棱都能作对角面，可作(n-3)个对角面，n条侧棱可作n(n-3)个对角面，由于这些对角面是相互之间重复计算了，‎ 所以共有n(n-3)÷2个对角面，‎ 所以可得f(n+1)-f(n)‎ ‎=(n+1)(n+1-3)÷2-n(n-3)÷2‎ ‎=n-1，‎ 故f(n+1)=f(n)+n-1.‎ ‎5.古希腊人常用小石子在沙滩上摆成各种形状来研究数.比如：‎ 他们研究过图1中的1，3，6，10，…，由于这些数能够表示成三角形，将其称为三角形数；类似地，称图2中的1，4，9，16，…，这样的数为正方形数.下列数中既是三角形数又是正方形数的是(　　)‎ A.289 B‎.1024 ‎ C.1225 D.1378‎ ‎【解析】选C.观察三角形数：1，3，6，10，…，记该数列为{an}，则a1=1，‎ a2=a1+2，‎ a3=a2+3，‎ ‎…‎ an=an-1+n.‎ 所以a1+a2+…+an ‎=(a1+a2+…+an-1)+(1+2+3+…+n)⇒an=1+2+3+…+n=，‎ 观察正方形数：1，4，9，16，…，记该数列为{bn}，‎ 则bn=n2.把四个选项的数字，分别代入上述两个通项公式，可知使得n都为正整数的只有1225.‎ ‎6.(2014·枣庄高二检测)将正奇数按如图所示的规律排列，则第21行从左向右的第5个数为(　　)‎ ‎1‎ ‎3　5　7‎ ‎9　11　13　15　17‎ ‎19　21　23　25　27　29　31‎ ‎…　‎ A.809 B‎.853 ‎ C.785 D.893‎ ‎【解析】选A.前20行共有正奇数1+3+5+…+39=202=400个，‎ 则第21行从左向右的第5个数是第405个正奇数，‎ 所以这个数是2×405-1=809.‎ 二、填空题(每小题4分，共12分)‎ ‎7.在平面上，若两个正三角形的边长的比为1∶2，则它们的面积比为1∶4.类似地，在空间中，若两个正四面体的棱长的比为1∶2，则它们的体积比为________.‎ ‎【解析】==·‎ ‎=×=.‎ 答案：‎ ‎8.(2014·石家庄高二检测)设n为正整数，f(n)=1+++…+，计算得f(2)=，f(4)>2，f(8)>，f(16)>3，观察上述结果，可推测一般的结论为________.‎ ‎【解析】由前四个式子可得，第n个不等式的左边应当为f(2n)，右边应当为，即可得一般的结论为f(2n)≥.‎ 答案：f(2n)≥‎ ‎9.(2014·杭州高二检测)对于命题“如果O是线段AB上一点，则||·+||·=‎0”‎将它类比到平面的情形是：若O是△ABC内一点，有S△OBC·+S△OCA·+S△OBA·=0，将它类比到空间的情形应为：若O是四面体ABCD内一点，则有____________________________.‎ ‎【解析】根据类比的特点和规律，所得结论形式上一致，又线段类比平面，平面类比到空间，又线段长类比为三角形面积，再类比成四面体的体积，故可以类比为 VO-BCD·+VO-ACD·+VO-ABD·+VO-ABC·=0.‎ 答案：VO-BCD·+VO-ACD·+VO-ABD·+VO-ABC·=0‎ 三、解答题(每小题10分，共20分)‎ ‎10.平面中的三角形和空间中的四面体有很多相类似的性质，例如在三角形中：‎ ‎(1)三角形两边之和大于第三边.‎ ‎(2)三角形的面积S=×底×高.‎ ‎(3)三角形的中位线平行于第三边且第于第三边的.‎ ‎…‎ 请类比上述性质，写出空间中四面体的相关结论.‎ ‎【解析】由三角形的性质，可类比得空间四面体的相关性质为：‎ ‎(1)四面体的任意三个面的面积之和大于第四个面的面积.‎ ‎(2)四面体的体积V=×底面积×高.‎ ‎(3)四面体的中位面平行于第四个面且面积等于第四个面的面积的.‎ ‎11.在平面几何中研究正三角形内任意一点与三边的关系时，我们有真命题：边长为a的正三角形内任意一点到各边的距离之和是定值a，类比上述命题，请你写出关于正四面体内任意一点与四个面的关系的一个真命题，并给出简要的证明.‎ ‎【解题指南】利用类比推理时，正三角形可类比成正四面体，归纳出结论再给予证明.‎ ‎【解析】类比所得的真命题是：棱长为a的正四面体内任意一点到四个面的距离之和是定值a.‎ 证明：设M是正四面体P-ABC内任一点，M到面ABC，面PAB，面PAC，面PBC的距离分别为d1，d2，d3，d4.‎ 由于正四面体四个面的面积相等，故有：‎ VP-ABC=VM-ABC+VM-PAB+VM-PAC+VM-PBC ‎=·S△ABC·(d1+d2+d3+d4)，‎ 而S△ABC=a2，VP-ABC=a3，‎ 故d1+d2+d3+d4=a(定值).‎ ‎【变式训练】设f(x)=，先分别求f(0)+f(1)，f(-1)+f(2)，f(-2)+f(3)，然后归纳出一个一般结论，并给出证明.‎ ‎【解析】f(0)+f(1)=+‎ ‎=+‎ ‎=+=.‎ 同理f(-1)+f(2)=，‎ f(-2)+f(3)=.‎ 由此猜想：当x1+x2=1时，‎ f(x1)+f(x2)=.‎ 证明：设x1+x2=1，‎ 则f(x1)+f(x2)=+‎ ‎=‎ ‎=‎ ‎=‎ ‎=.‎ 故猜想成立.‎ 一、选择题(每小题4分，共16分)‎ ‎1.(2014·厦门高二检测)定义A*B，B*C，C*D，D*A的运算分别对应下图中的(1)，(2)，(3)，(4)，那么下图中的(A)，(B)所对应的运算结果可能是(　　)‎ A.B*D，A*D B.B*D，A*C C.B*C，A*D D.C*D，A*D ‎【解析】选B.由(1)(2)(3)(4)图得A表示|，B表示□，C表示—，D表示○，故图(A)(B)表示B*D和A*C.‎ ‎2.(2014·西安高二检测)已知“整数对”按如下规律排成一列：‎ ‎(1，1)，(1，2)，(2，1)，(1，3)，(2，2)，(3，1)，(1，4)，(2，3)，(3，‎ ‎2)，(4，1)，…，则第60个数对是(　　)‎ A.(7，5) B.(5，7)‎ C.(2，10) D.(10，1)‎ ‎【解析】选B.依题意，由和相同的“整数对”分为一组不难得知，第n组“整数对”的和为n+1，且有n个“整数对”.这样前n组一共有个“整数对”.注意到<60<.因此第60个“整数对”处于第11组的第5个位置，可得为(5，7).‎ ‎3.(2014·汕头高二检测)观察下列各式：‎ ‎1=12，‎ ‎2+3+4=32，‎ ‎3+4+5+6+7=52，‎ ‎4+5+6+7+8+9+10=72，‎ ‎…，‎ 可以得出的一般结论是(　　)‎ A.n+(n+1)+(n+2)+…+(3n-2)=n2‎ B.n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2‎ C.n+(n+1)+(n+2)+…+(3n-1)=n2‎ D.n+(n+1)+(n+2)+…+(3n-1)=(2n-1)2‎ ‎【解析】选B.可以发现：第一个式子的第一个数是1，第二个式子的第一个数是2，…故第n个式子的第一个数是n；第一个式子中有1个数相加，第二个式子中有3个数相加，…故第n个式子中有2n-1个数相加；第一个式子的结果是1的平方，第二个式子的结果是3的平方，…故第n个式子应该是2n-1的平方，故可以得到n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2.‎ ‎4.(2014·临沂高二检测)已知x>0，由不等式x+≥2=2，x+=++≥3=3，…我们可以得出推广结论：x+≥n+1(n∈N*)，则a=(　　)‎ A.2n B.n‎2 ‎ C.3n D.nn ‎【解析】选D.再续写一个不等式：‎ x+=+++≥‎ ‎4=4，‎ 由此可得a=nn.‎ 二、填空题(每小题5分，共10分)‎ ‎5.已知经过计算和验证有下列正确的不等式：+<2，+<2，+<2，根据以上不等式的规律，请写出一个对正实数m，n都成立的条件不等式_____________________.‎ ‎【解析】观察所给不等式可以发现：不等式左边两个根式的被开方数的和等于20，不等式的右边都是2，因此对正实数m，n都成立的条件不等式是：若m>0，n>0，则当m+n=20时，有+<2.‎ 答案：若m>0，n>0，则当m+n=20时，有+<2‎ ‎6.在Rt△ABC中，若∠C=90°，AC=b，BC=a，则△ABC外接圆半径r=.运用类比方法，若三棱锥的三条侧棱两两互相垂直且长度分别为a，b，c，则其外接球的半径R=________.‎ ‎【解题指南】解题时题设条件若是三条线两两互相垂直，就要考虑到构造正方体或长方体.‎ ‎【解析】(构造法)通过类比可得R=.‎ 证明：作一个在同一个顶点处棱长分别为a，b，c的长方体，则这个长方体的体对角线的长度是，故这个长方体的外接球的半径是，这也是所求的三棱锥的外接球的半径.‎ 答案：‎ ‎【变式训练】在平面几何里，有“若△ABC的三边长分别为a，b，c，内切圆半径为r，则三角形面积为S△ABC=(a+b+c)r”，拓展到空间，类比上述结论，“若四面体ABCD的四个面的面积分别为S1，S2，S3，S4，内切球的半径为R，则四面体的体积为________”.‎ ‎【解题指南】注意发现其中的规律总结出共性加以推广，或将结论类比到其他方面，得出结论.‎ ‎【解析】三角形的面积类比为四面体的体积，三角形的边长类比为四面体四个面的面积，内切圆半径类比为内切球的半径.二维图形中类比为三维图形中的，得V四面体ABCD=(S1+S2+S3+S4)R.‎ 答案：V四面体ABCD=(S1+S2+S3+S4)R 三、解答题(每小题12分，共24分)‎ ‎7.观察下列等式：‎ ‎①sin210°+cos240°+sin10°cos40°=；‎ ‎②sin26°+cos236°+sin6°cos36°=.‎ 由上面两题的结构规律，你能否提出一个猜想?并证明你的猜想.‎ ‎【解析】由①②可看出，两角差为30°，‎ 则它们的相关形式的函数运算式的值均为.‎ 猜想：若β-α=30°，‎ 则β=30°+α，sin2α+cos2β+sinαcosβ=，‎ 也可直接写成sin2α+cos2(α+30°)+sinαcos(α+30°)=.‎ 下面进行证明：‎ 左边=++sinαcos(α+30°)‎ ‎=++‎ sinα·(cosα·cos30°-sinαsin30°)‎ ‎=-cos2α++cos2α-sin2α+sin2α-==右边.‎ 故sin2α+cos2(α+30°)+sinαcos(α+30°)=.‎ ‎8.某少数民族的刺绣有着悠久的历史，如图(1)，(2)，(3)，(4)为最简单的四个图案，这些图案都是由小正方形构成，小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同)，设第n个图形包含f(n)个小正方形.‎ ‎(1)求出f(5)的值.‎ ‎(2)利用合情推理的“归纳推理思想”，归纳出f(n+1)与f(n)之间的关系式，并根据你得到的关系式求出f(n)的表达式.‎ ‎(3)求+++…+的值.‎ ‎【解析】(1)f(5)=41.‎ ‎(2)因为f(2)-f(1)=4=4×1，‎ f(3)-f(2)=8=4×2，‎ f(4)-f(3)=12=4×3，‎ f(5)-f(4)=16=4×4，‎ ‎…‎ 由上式规律，所以得出f(n+1)-f(n)=4n.‎ 因为f(n+1)-f(n)=4n⇒f(n+1)=f(n)+4n⇒‎ f(n)=f(n-1)+4(n-1)‎ ‎=f(n-2)+4(n-1)+4(n-2)‎ ‎=f(n-3)+4(n-1)+4(n-2)+4(n-3)‎ ‎=…‎ ‎=f(1)+4(n-1)+4(n-2)+4(n-3)+…+4‎ ‎=2n2-2n+1.‎ ‎(3)当n≥2时，=‎ ‎=.‎ 所以+++…+‎ ‎=1+×‎ ‎=1+=-.‎ 关闭Word文档返回原板块