2017-2018学年河南省南阳市第一中学高二上学期第三次月考数学（理）试题（解析版）

2017-2018学年河南省南阳市第一中学高二上学期第三次月考数学（理）试题（解析版）

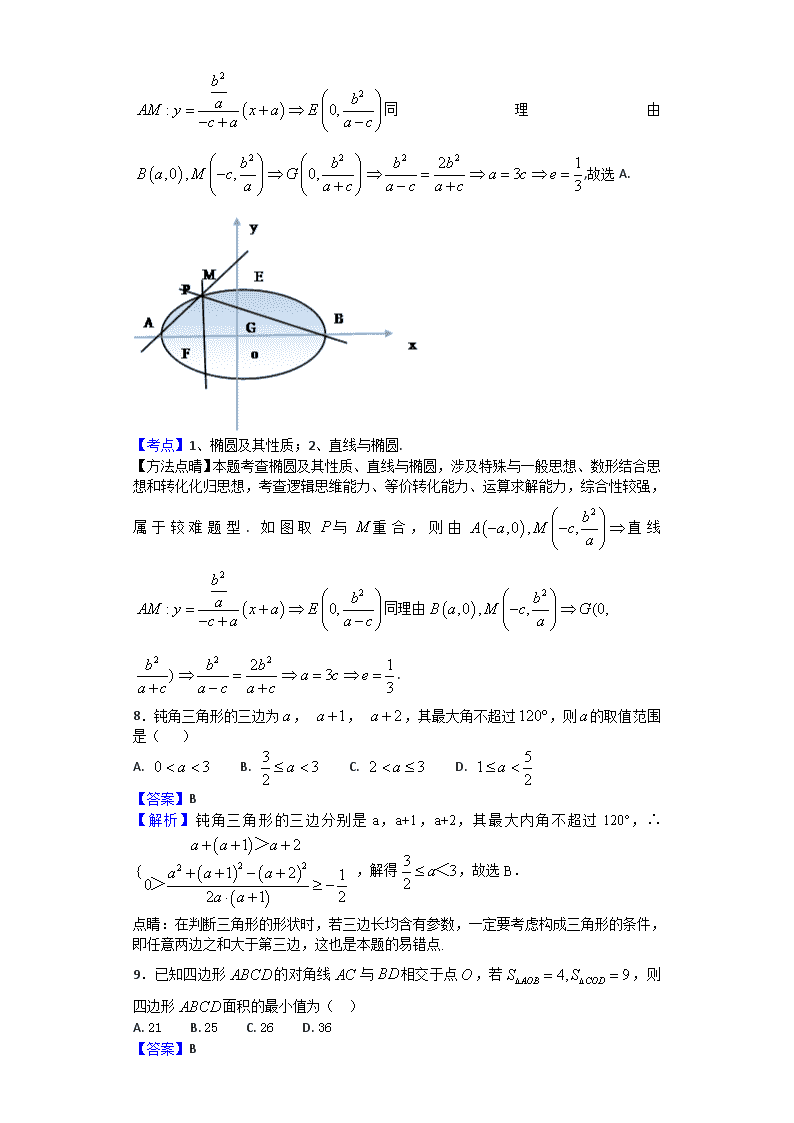
‎2017-2018学年河南省南阳市第一中学高二上学期第三次月考数学（理）试题 一、单选题 ‎1．抛物线的准线方程为y=2，则a的值为（ ）‎ A. B. C. 8 D. －8‎ ‎【答案】B ‎【解析】抛物线的标准方程是，则其准线方程为，所以，‎ 故选A.‎ ‎2．不等式的解集是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】不等式等价于 ‎ 故答案为：D。‎ ‎3．夏季山上气温从山脚起每升高‎100米，降低‎0.7℃‎，已知山顶气温是‎14.1℃‎，山脚下气温是‎26℃‎，那么山顶相对山脚的高度是 （ ）‎ A、‎1500米 B、‎1600米 C、‎1700米 D、‎‎1800米 ‎【答案】C.‎ ‎【解析】由（米）,知应选C.‎ ‎4．等差数列共有项，若前项的和为200，前项的和为225，则中间项的和为（ ）‎ A. 50 B. 75 C. 100 D. 125‎ ‎【答案】B ‎【解析】设等差数列前m项的和为x，由等差数列的性质可得，中间的m项的和可设为x+d，后m项的和设为x+2d，‎ 由题意得2x+d=200，3x+3d=225，‎ 解得x=125，d=﹣50，‎ 故中间的m项的和为75，‎ 故选B．‎ ‎5．满足的恰有一个，则的取值范围是（ ）‎ A. B. C. D. 或 ‎【答案】B ‎【解析】根据正弦定理得到 ‎ ‎ 画出和 的图像，使得两个函数图象有一个交点即可；此时的取值范围是。‎ 故选B．‎ ‎6．已知等比数列中， ， ，则的值为（ ）‎ A. 2 B. 4 C. 8 D. 16‎ ‎【答案】A ‎【解析】由等比数列的性质得到 ‎ 又因为 ‎ 故得到原式等于 ‎ ‎ ‎ 代入上式得到 故答案为：A。‎ 点睛：这个题目考查的是等比数列的性质和应用；解决等差等比数列的小题时，常见的思路是可以化基本量，解方程；利用等差等比数列的性质解决题目；还有就是如果题目中涉及到的项较多时，可以观察项和项之间的脚码间的关系，也可以通过这个发现规律。‎ ‎7．已知为坐标原点， 是椭圆的左焦点， 分别为的左，右顶点． 为上一点，且轴过点的直线与线段交于点，与轴交于点．若直线经过的中点，则的离心率为（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】A ‎【解析】试题分析：如图取与重合，则由直线 同理由,故选A.‎ ‎【考点】1、椭圆及其性质；2、直线与椭圆.‎ ‎【方法点晴】本题考查椭圆及其性质、直线与椭圆，涉及特殊与一般思想、数形结合思想和转化化归思想，考查逻辑思维能力、等价转化能力、运算求解能力，综合性较强，属于较难题型. 如图取与重合，则由直线同理由 ‎.‎ ‎8．钝角三角形的三边为， ， ，其最大角不超过，则的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】钝角三角形的三边分别是a，a+1，a+2，其最大内角不超过120°，∴，解得，故选B．‎ 点睛：在判断三角形的形状时，若三边长均含有参数，一定要考虑构成三角形的条件，即任意两边之和大于第三边，这也是本题的易错点.‎ ‎9．已知四边形的对角线与相交于点，若，则四边形面积的最小值为（ ）‎ A. 21 B. 25 C. 26 D. 36‎ ‎【答案】B ‎【解析】设点A到边BD的距离为h．‎ 任意四边形ABCD中，S△AOB=4，S△COD=9；‎ ‎∵S△AOD=OD•h，S△AOB=OB•h=4，‎ ‎∴S△AOD=OD•=4×，S△BOC=OB•=9×；‎ 设=x，则S△AOD=4x，S△BOC=；‎ ‎∴S四边形ABCD=4x++13≥2•+13=12+13=25；‎ 故四边形ABCD的最小面积为25．‎ 故选B．‎ ‎10．已知为抛物线上一个动点，直线：，：，则到直线、的距离之和的最小值为 ( ). ‎ A． B． C． D．‎ ‎【答案】A ‎【解析】试题分析：将P点到直线l1：x=-1的距离转化为P到焦点F（1，0）的距离，过点F作直线l2垂线，交抛物线于点P，此即为所求最小值点，∴P到两直线的距离之和的最小值为=，故选A．‎ ‎【考点】本题考查了直线和圆锥曲线的位置关系 点评：解题时要认真审题，注意抛物线定义及点到直线距离公式的灵活运用．‎ ‎11．已知等差数列有无穷项，且每一项均为自然数，若75，99，235为中的项，则下列自然数中一定是中的项的是（ ）‎ A. 2017 B. 2019 C. 2021 D. 2023‎ ‎【答案】B ‎【解析】因为数列是等差数列，而75，99，235，是数列中的三项，故得到每两项的差一定是公差的整数倍，99-75=24，235-75=160，235-99=136.即24，160，136，均是公差的整数倍，可求这三个的最大公约数8，故得到公差为8.首项为3，2019-3=2016，2016是8的252倍，而其它选项减去3之后均不是8的倍数.故答案为：2019.‎ 故答案为：B。‎ 点睛：这个题目考查的是等差数列的性质和应用；解决等差等比数列的小题时，常见的思路是可以化基本量，解方程；利用等差等比数列的性质解决题目；还有就是如果题目中涉及到的项较多时，可以观察项和项之间的脚码间的关系，也可以通过这个发现规律。‎ 二、填空题 ‎12．设，满足约束条件且的最小值为7，则 ‎（A）-5 （B）3 （C）-5或3 （D）5或-3‎ ‎【答案】B ‎【解析】试题分析：根据题中约束条件可画出可行域如下图所示，两直线交点坐标为：，又由题中可知，当时，z有最小值：，则，解得：;当时，z无最小值．故选B ‎【考点】线性规划的应用 ‎13．若等差数列满足，则当__________时的前项和最大．‎ ‎【答案】8‎ ‎【解析】由条件知道，因为数列是等差数列，故公差小于0或者大于0， ‎ 故得到 符号相反，故，故数列中前8项大于0，从第九项开始小于0，故得到前8项的和最大。‎ 故答案为：8.‎ ‎14．在中，内角所对应的边分别为，已知，若，则的值为__________．‎ ‎【答案】‎ ‎【解析】由正弦定理得到， ，因为三角形内角的正弦值都是大于0的，故得到 ， ‎ ‎，代入表达式得到。‎ 故答案为： 。‎ ‎15．是椭圆与双曲线的公共焦点分别是在第二、四象限的公共点，若四边形为矩形，则的离心率是__________．‎ ‎【答案】‎ ‎【解析】设椭圆中的基本量为，双曲线中的基本量为 ‎ 由圆锥曲线中焦三角形的面积公式得到 C=,,的离心率是 ‎ 故答案为： 。‎ ‎16．， 为两个定点， 是的一条切线，若过两点的抛物线以直线为准线，则该抛物线的焦点的轨迹方程是__________．‎ ‎【答案】‎ ‎【解析】根据题意画出图像，任意画出一条切线，做AB垂直于切线于CD两点，设抛物线的焦点为F点，根据抛物线的定义得到， ，因为O为AB的中点，做OG垂直于切线于点G，OG为梯形ABCE的中位线，故得到BF+AF=2OG=8，故根据椭圆的定义得到轨迹是以AB为焦点的椭圆长半轴为4，c=2,故得到轨迹方程为，由条件知焦点一定不能落在x轴上故需要去掉两点。‎ 故答案为： 。‎ 点睛：这道题目圆锥曲线中的求轨迹方程的方法；常见的方法有：数形结合法即几何法；相关点法， 直接法；定义法，代入法，引入参数再消参的方法，交轨法是一种解决两直线交点的轨迹的方法，也是一种消参的方法。‎ 三、解答题 ‎17．（1）求对称轴是轴，焦点在直线上的抛物线的标准方程； ‎ ‎（2）过抛物线焦点的直线它交于两点，求弦的中点的轨迹方程.‎ ‎【答案】（1）；（2）.‎ ‎【解析】试题分析：（1）根据题意知道焦点就是直线和x轴的交点，根据抛物线的定义得到方程即可；‎ ‎（2）先考虑直线的斜率不存在时的情况；再考虑直线斜率存在时，联立直线和抛物线根据韦达定理得到中点坐标为，再消参即可。‎ 解析：‎ ‎（1）对称轴是轴则顶点在焦点在轴 所以，则， ，‎ ‎.‎ ‎（2）由题知抛物线焦点为，‎ 当直线的斜率存在时，设为，则焦点弦方程为，‎ 代入抛物线方程得所以，由题意知斜率不等于0，‎ 方程是一个一元二次方程，由韦达定理： ‎ 所以中点坐标： ‎ 代入直线方程 中点纵坐标； ‎ 即中点为 消参数，得其方程为 当直线的斜率不存在时，直线的中点是，符合题意，‎ 综上所述，答案为.‎ ‎18．在中，角所对的边分别为，已知.‎ ‎（1）求角的大小；‎ ‎（2）求的最大值.‎ ‎【答案】（1）；（2）6.‎ ‎【解析】试题分析：（1）首先将正切化为正弦，得到，再将式子化简得到，进而得到角A ；（2）由余弦定理得到，由不等式放缩得到最终结果。‎ 解析：‎ ‎（1）在中，∵，∴整理可得： ，‎ ‎∴，∴，‎ ‎∴，∴，可得： .‎ ‎（2）由（1），根据余弦定理可得：‎ ‎，∴解得： ，‎ ‎∴，当且仅当时， ，故的最大值为6.‎ ‎19．若数列的首项为1，且.‎ ‎（1）求证： 是等比数列；‎ ‎（2）求数列的通项公式；‎ ‎（3）若，求证：数列的前项和.‎ ‎【答案】（1）见解析；（2）；（3）见解析.‎ ‎【解析】试题分析：（1）将式子变形为，进而得到数列为等比数列（2）有第一问得到是等比数列，故得到；（3）根据第二问可求出，再错位相减，得到和，最终证得结果。‎ 解析：‎ ‎（1）由得，‎ ‎∴， ，∴， ，‎ ‎∴是首项为公比为的等比数列 ‎（2）由（1）知，∴‎ ‎（3）∵‎ ‎， ‎ ‎∴ ‎ ‎ ∴.‎ ‎20．已知数列中， .‎ ‎（1）求证：数列与都是等比数列；‎ ‎（2）若数列的前项和为.令，求数列的最大项.‎ ‎【答案】（1）见解析；（2）.‎ ‎【解析】试题分析：（1）由递推公式得到， ，两式作比得到隔项成等比数列（2）由第一问得到数列. 的前项和为的表达式，代入得到 ‎，通过两项做差可得数列的单调性，进而得到最大项为第二项。‎ 解析：‎ ‎（1）证明：数列中， ，‎ ‎，‎ ‎∴，‎ ‎∴，‎ ‎∵，∴，‎ ‎∴数列是以1为首项，以为公比的等比数列，‎ 数列是以为首项，以为公比的等比数列.‎ ‎（2）解：由（1）得 ‎.‎ ‎∴‎ ‎，‎ ‎，‎ ‎∴‎ ‎，‎ ‎∴，‎ ‎∴.‎ ‎21．已知动圆过定点，且在定圆的内部与其相内切.‎ ‎（1）求动圆圆心的轨迹方程；‎ ‎（2）直线与交于两点，与圆交于两点，求的值.‎ ‎【答案】（1）；（2）.‎ ‎【解析】试题分析：（1）根据题意画出图像，根据图像的几何关系得到P点的轨迹；（2）联立直线和椭圆根据弦长公式求得弦长，根据垂径定理得到GH的长，从而得到结果。‎ 解析：‎ ‎（1）如图所示，设动圆和定圆内切于点.动点到两定点，即定点 和定圆圆心距离之和恰好等于定圆半径，‎ 即，‎ ‎∴点的轨迹是以为两焦点，半长轴为2，半短轴长为的椭圆： .‎ ‎（2）将代入得， ，‎ 所以，又由垂径定理得，‎ ‎，所以.‎ 点睛：本题是先根据椭圆的定义，判定轨迹是椭圆，然后根据椭圆的标准方程，求轨迹的方程．这是求轨迹方程的一种重要思想方法，应该熟练并灵活运用．求轨迹常用方法有：相关点法，几何方法等。‎ ‎22．已知点为坐标原点， 是椭圆上的两个动点，满足直线与直线关于直线对称.‎ ‎（1）证明直线的斜率为定值，并求出这个定值；‎ ‎（2）求的面积最大时直线的方程.‎ ‎【答案】（1）直线的斜率为定值，其值为；（2），或.‎ ‎【解析】试题分析：（1）联立直线和椭圆，解出两个的交点坐标，用两点坐标解出直线斜率；（2）联立直线和椭圆根据弦长公式得到.‎ 再根据点到直线的距离得到，此时面积为，进而得到结果。‎ 解析：‎ ‎（1）设直线方程为： ，代入得 设，因为点在椭圆上，所以 又由题知，直线的斜率与的斜率互为相反数，在上式中以代，可得 ‎，‎ 所以直线的斜率 即直线的斜率为定值，其值为.‎ ‎（2）由（1）可设直线方程为： ，代入得 ‎，则.由可得.‎ ‎， 到直线的距离，‎ 可得，‎ 当且仅当（满足），即时取等，此时直线的方程为： ，或.‎ 点睛：圆锥曲线中最值与范围问题的常见求法：(1)几何法：若题目的条件和结论能明显体现几何特征和意义，则考虑利用图形性质来解决；(2)代数法：若题目的条件和结论能体现一种明确的函数关系，则可首先建立目标函数，再求这个函数的最值．在利用代数法解决最值与范围问题时常从以下几个方面考虑：①利用判别式来构造不等关系，从而确定参数的取值范围；②利用隐含或已知的不等关系建立不等式，从而求出参数的取值范围；③利用基本不等式求出参数的取值范围；④利用函数的值域的求法，确定参数的取值范围．‎