2013届人教A版理科数学课时试题及解析（10）函数与方程

2013届人教A版理科数学课时试题及解析（10）函数与方程

课时作业(十)　[第10讲　函数与方程]‎ ‎[时间：45分钟　　分值：100分]‎ ‎1． 若函数f(x)＝x2＋2x＋‎3a没有零点，则实数a的取值范围是(　　)‎ A．a＜ B．a＞ C．a≤ D．a≥ ‎2．已知[x]表示不超过实数x的最大整数，g(x)＝[x]为取整函数，x0是函数f(x)＝lnx－的零点，则g(x0)等于(　　)‎ A．1 B．‎2 C．3 D．4‎ ‎3． 设f(x)＝x3＋bx＋c(b>0)(－1≤x≤1)，且f·f<0，则方程f(x)＝0在[－1,1]内(　　)‎ A．可能有3个实数根 B．可能有2个实数根 C．有唯一的实数根 D．没有实数根 ‎4．已知二次函数f(x)＝x2－(m－1)x＋‎2m在[0,1]上有且只有一个零点，则实数m的取值范围为(　　)‎ A．(－2,0) B．(－1,0)‎ C．[－2,0] D．(－2，－1)‎ ‎5． 已知三个函数f(x)＝2x＋x，g(x)＝x－2，h(x)＝log2x＋x的零点依次为a，b，c，则(　　)‎ A．a1 D．00，f(0.687 5)<0，则可得到方程精确度为0.1的一个近似解是________．‎ ‎12． 已知函数f(x)＝ex－2x＋a有零点，则a的取值范围是________．‎ ‎13．已知函数f(x)＝－x2－2x，g(x)＝若方程g[f(x)]－a＝0的实数根的个数有4个，则a的取值范围是________．‎ ‎14．(10分)已知函数f(x)＝4x＋m·2x＋1有且仅有一个零点，求m的取值范围，并求出该零点．‎ ‎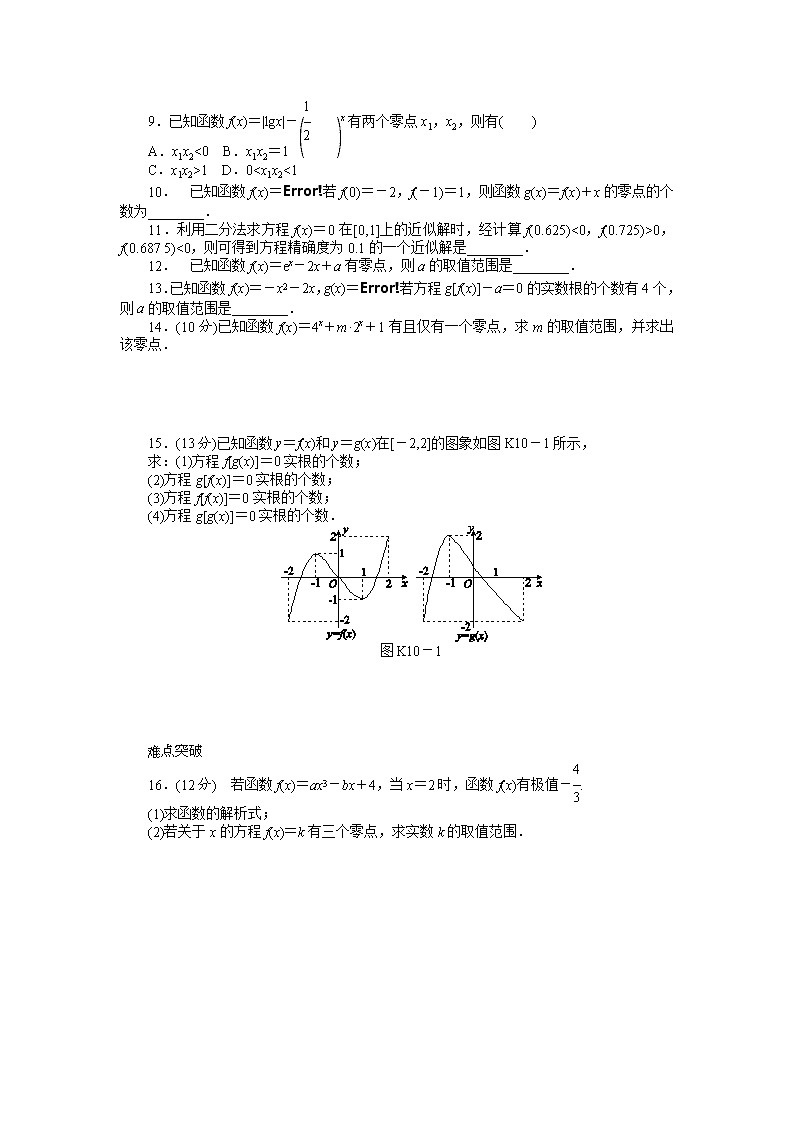15．(13分)已知函数y＝f(x)和y＝g(x)在[－2,2]的图象如图K10－1所示，‎ 求：(1)方程f[g(x)]＝0实根的个数；‎ ‎(2)方程g[f(x)]＝0实根的个数；‎ ‎(3)方程f[f(x)]＝0实根的个数；‎ ‎(4)方程g[g(x)]＝0实根的个数．‎ 图K10－1‎ ‎16．(12分) 若函数f(x)＝ax3－bx＋4，当x＝2时，函数f(x)有极值－.‎ ‎(1)求函数的解析式；‎ ‎(2)若关于x的方程f(x)＝k有三个零点，求实数k的取值范围．‎ 课时作业(十)‎ ‎【基础热身】‎ ‎1．B　[解析] 由题意，函数f(x)＝x2＋2x＋‎3a没有零点，即方程x2＋2x＋‎3a＝0无解，即方程的判别式小于零，解不等式Δ＝22－4×‎3a＜0，得a＞.‎ ‎2．B　[解析] 因为f(2)＝ln2－1<0，f(3)＝ln3－>0，故x0∈(2,3)，g(x0)＝[x0]＝2.‎ ‎3．C　[解析] ∵f(x)＝x3＋bx＋c(b>0)，‎ ‎∴f′(x)＝3x2＋b>0，∴f(x)在[－1,1]上为增函数，‎ 又∵f·f<0，‎ ‎∴f(x)在[－1,1]上有实数根且只有一个．‎ ‎4．C　[解析] (1)当方程x2－(m－1)x＋‎2m＝0在[0,1]上有两个相等实根时，Δ＝(m－1)2－‎8m＝0且0≤≤1，此时无解．‎ ‎(2)当方程x2－(m－1)x＋‎2m＝0有两个不相等的实根时，①有且只有一根在(0,1)上时，有f(0)f(1)<0，即‎2m(m＋2)<0，解得－20，故f(x)＝2x＋x的零点a∈(－1,0)；因为g(2)＝0，故g(x)的零点b＝2；因为h＝－1＋＝－<0，h(1)＝1>0，故h(x)的零点c∈，因此a0，‎ f＝－4<0，f(0)＝－2<0，f＝－1>0，f＝e>0，‎ ‎∴f(x)定在内存在唯一零点．‎ ‎8．B　[解析] 如图，当x∈[0,5]时，结合图象知f(x)与g(x)共有5个交点，故在区间[－5,0]上共有5个交点；当x∈(0,10]时结合图象知共有9个交点．故函数h(x)＝f(x)－g(x)在区间[－5,10]上共有14个零点．‎ ‎9．D　[解析] 数形结合，可知函数f(x)的两个零点分别在区间(0,1)，(1，＋∞)．去掉绝对值符号后，再根据函数的性质寻找其中的关系．根据分析，不妨设01，根据函数零点的概念则有|lgx1|－x1＝0，|lgx2|－x2＝0，即－lgx1＝x1，lgx2＝x2，后面的方程减去前面的方程得lg(x1x2)＝x2－x1.由于x2>x1，根据指数函数的性质 ‎，x2－x1<0，所以lg(x1x2)<0，即00，此时g(x)为增函数；当x∈(ln2，＋∞)时，g′(x)＝－ex＋2<0，此时g(x)为减函数．‎ 所以，当x＝ln2时，函数g(x)＝－ex＋2x有最大值2ln2－2，即g(x)＝－ex＋2x的值域为(－∞，2ln2－2]，所以a∈(－∞，2ln2－2]．‎ ‎13.　[解析] 由于函数f(x)＝－x2－2x＝－(x＋1)2＋1≤1，只有f(x)＝t，t<1时，方程f(x)＝t才有两个不同的实根，这样问题就等价于方程g(t)＝a有两个小于1的不等实根，画出函数g(x)的图象如图，数形结合得1≤a<.‎ ‎14．[解答] ∵f(x)＝4x＋m·2x＋1有且仅有一个零点，‎ 即方程(2x)2＋m·2x＋1＝0仅有一个实根．‎ 设2x＝t(t>0)，则t2＋mt＋1＝0.‎ 当Δ＝0，即m2－4＝0时，‎ m＝－2时，t＝1；m＝2时，t＝－1，不合题意，舍去，‎ ‎∴2x＝1，x＝0，符合题意．‎ 当Δ>0，即m>2或m<－2时，‎ t2＋mt＋1＝0应有一正一负两根，‎ 即t1t2<0，这与t1t2＝1>0矛盾．‎ ‎∴这种情况不可能．‎ 综上可知：m＝－2时，f(x)有唯一零点，该零点为x＝0.‎ ‎15．[解答] (1)满足f(x)＝0的x值在区间[－2,2]上有三个，把这三个看做g(x)对应的y值，则g(x)等于这三个值的每个x都有两个，故方程f[g(x)]＝0有且仅有6个根．‎ ‎(2)满足g(x)＝0的x值有两个，一个在区间(－2，－1)上，一个在区间(0,1)上，把这两个看做f(x)对应的y值，f(x)等于这两个x值时，在区间(－2，－1)上只有一个x与之对应，在区间(0,1)上有三个x与之对应，故方程g[f(x)]＝0有且只有4个根．‎ ‎(3)满足f(x)＝0的x值在区间[－2,2]上有三个，把这三个再看做f(x)对应的y值，在区间(－2，－1)上只有一个x值，在区间(1,2)上也只有一个x值，而f(x)＝0所对应的x值有三个，故方程f[f(x)]＝0有且仅有5个根．‎ ‎(4)同样的方法可知方程g[g(x)]＝0有且仅有4个根．‎ ‎【难点突破】‎ ‎16．[解答] (1)由题意可知f′(x)＝3ax2－b，‎ 于是解得 故所求的解析式为f(x)＝x3－4x＋4.‎ ‎(2)由(1)可知f′(x)＝x2－4＝(x－2)(x＋2)，‎ 令f′(x)＝0，得x＝2或x＝－2.‎ 当x变化时f′(x)、f(x)的变化情况如下表所示：‎ x ‎(－∞，－2)‎ ‎－2‎ ‎(－2,2)‎ ‎2‎ ‎(2，＋∞)‎ f′(x)‎ ‎＋‎ ‎0‎ ‎－‎ ‎0‎ ‎＋‎ f(x)‎ 单调递增 单调递减 ‎－ 单调递增 因此，当x＝－2时，f(x)有极大值；‎ 当x＝2时，f(x)有极小值－.‎ 所以函数的大致图象如图．‎ 故实数k的取值范围是－＜k＜.‎ ‎ ‎