江西省上饶市2020届高三数学(理)第三次模拟试卷(Word版附答案)
www.ks5u.com
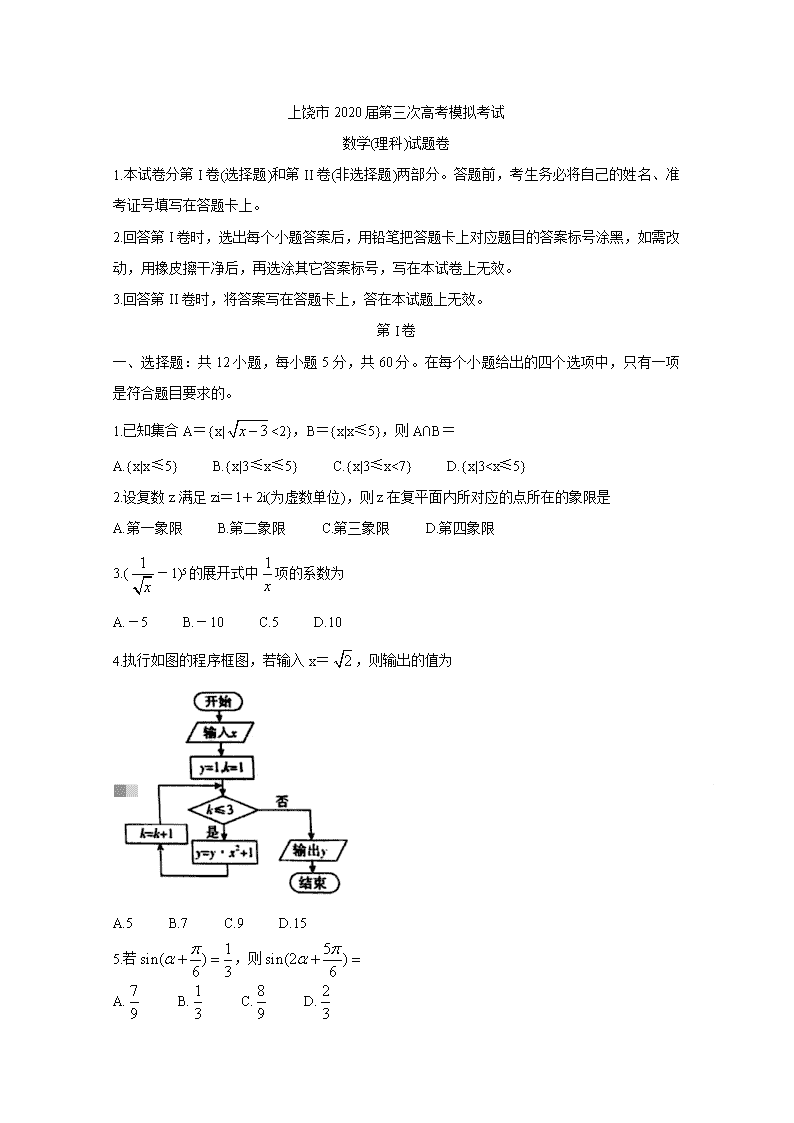
上饶市2020届第三次高考模拟考试
数学(理科)试题卷
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每个小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,写在本试卷上无效。
3.回答第II卷时,将答案写在答题卡上,答在本试题上无效。
第I卷
一、选择题:共12小题,每小题5分,共60分。在每个小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={x|<2},B={x|x≤5},则A∩B=
A.{x|x≤5} B.{x|3≤x≤5} C.{x|3≤x<7} D.{x|3
0的解集为
A.[-π,-3)∪(1,π] B.[-π,-1)∪(3,π] C.(-3,1) D.(-1,3)
10.半径为2的球O内有一个内接正三棱柱,则正三棱柱的侧面积的最大值为
A.9 B.12 C.16 D.18
11.已知双曲线C:的左、右焦点分别为F1,F2,过F1作斜率为的直线l与双曲线C的左、右两支分别交于A、B两点,若|AF2|=|BF2|,则双曲线的离心率为
A.2 B. C. D.
12.已知函数y=ex+和函数(a∈R),关于这两个函数图像的交点个数,下列四个结论:①当时a<2,两个函数图像没有交点;②当时,两个函数图像恰有三个交点;③当2时,两个函数图像恰有四个交点。正确结论的个数为
A.1 B.2 C.3 D.4
第II卷
二、填空题:本大题共四小题,每小题5分,共20分。
13.对于正在培育的一颗种子,它可能1天后发芽,也可能2天后发芽,…,如表是20颗不同种子发芽前所需培育的天数统计表,则这组种子发芽前所需培育的天数的众数是________。中位数是________(本题第一空2分,第二空3分)
14.若实数x,y满足条件,则z=3x+2y的最大值为________。
15.在扇形OAB中,∠AOB=60°,C为弧AB上的一个动点。若,则2x+y的取值范围是________。
16.正方形ABCD的两个顶点A,B在直线x+y-4=0上,另两个顶点C,D分别在直线2x-y-1=0,4x+y-23=0上,那么正方形ABCD的边长为________。
三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
17.(本小题满分12分)已知△ABC的内角A,B,C的对边分别为a,b,c,且满足sin2C+2sin2C=,C为锐角。
(1)求角C的大小;
(2)若cos∠BAC=-,点D为边BC上的动点(不与C点重合),设AD=λDC,求λ的取值范围。
18.(本小题满分12分)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,BC//AD,∠BAD=,PA=AB=BC=2,AD=4,点M是棱PD的中点。
(1)求证:CM//平面PAB;
(2)求二面角M-AC-D的大小。
19.(本小题满分12分)为了释放学生压力,某校高三年级一班进行了一个投篮游戏,其间甲、乙两人轮流进行篮球定点投篮比赛(每人各投一次为一轮)。在相同的条件下,每轮甲乙两人站在同一位置上,甲先投。每人投一次篮,两人有1人命中,命中者得1分,未命中者得-1分;两人都命中或都未命中,两人均得0分。设甲每次投篮命中的概率为,乙每次投篮命中的概率为,且各次投篮互不影响。
(1)经过1轮投篮,记甲的得分为X,求X的分布列及期望;
(2)若经过n轮投篮,用pi表示第i轮投篮后,甲的累计得分低于乙的累计得分的概率。
①求p1·p2·p3;
②规定p0=0,经过计算机模拟计算可得pi=api+1+bpi-1(i≥l,i∈N),请根据①中p1·p2·p3值求出a,b的值,并由此求出数列{pn}的通项公式。
20.(本小题满分12分)已知抛物线C:y2=2px(p>0)的焦点为F,抛物线C上的点到准线的最小距离l。
(1)求抛物线C的方程:
(2)若过点F作互相垂直的两条直线l1、l2,l1与抛物线C交于A,B两点,l2与抛物线C交于C,D两点,M,N分别为弦AB,CD的中点,求|MF|·|NF|的最小值。
21.(本小题满分12分)已知函数f(x)=ax+lnx2(a∈R)。
(1)讨论函数f(x)的单调区间情况;
(2)若函数f(x)=ax+lnx2(a≠0)有且只有两个零点x1,x2,证明:e-1<|x1+x2|0,ρ2>0,0≤θ1<2π,0≤θ2<2π),使点M、N到l的距离都为1?若存在,求出|θ1-θ2|的值;若不存在,请说明理由。
23.[选修4-5:不等式选讲](10分)设函数f(x)=cosx+|a-2|+|a+1|。
(1)若f()>,求实数a的取值范围;
(2)证明:对于任意的x∈R,f(x)≥|a-2|-|-1|成立。