2020届二轮复习椭圆、双曲线、抛物线教案(全国通用)
2020届二轮复习 椭圆、双曲线、抛物线 教案(全国通用)
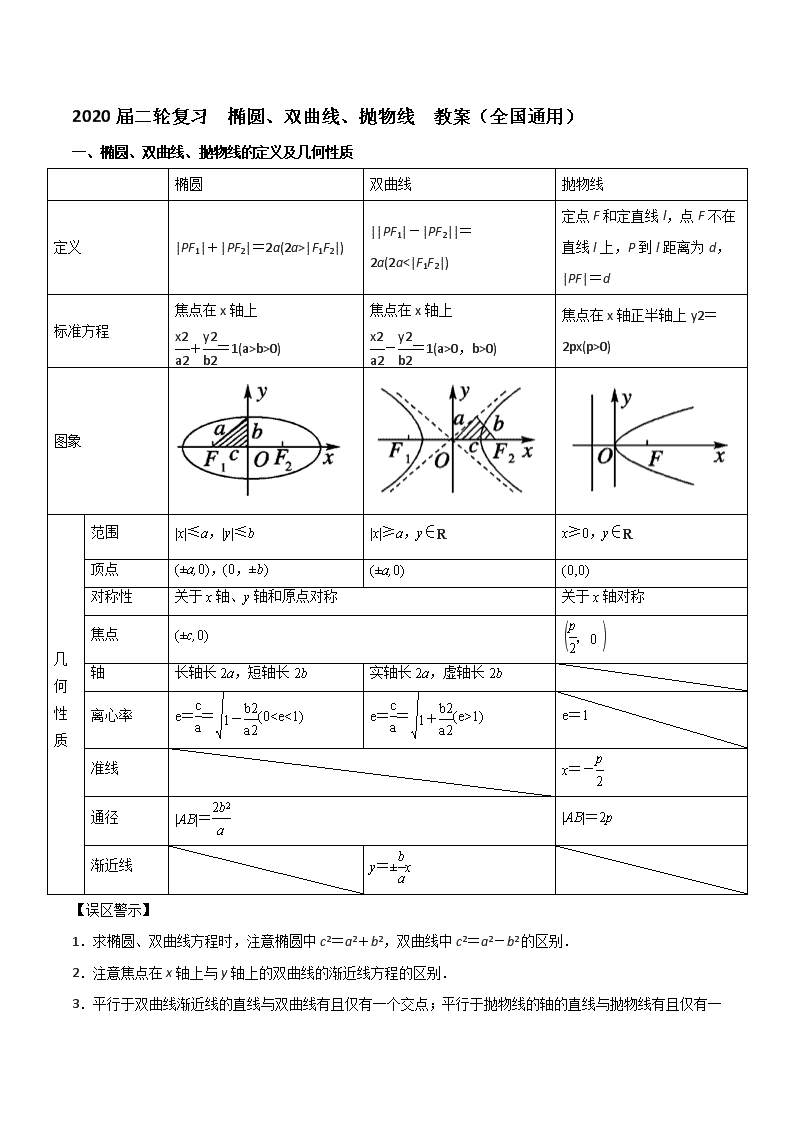
一、椭圆、双曲线、抛物线的定义及几何性质
椭圆
双曲线
抛物线
定义
|PF1|+|PF2|=2a(2a>|F1F2|)
||PF1|-|PF2||=2a(2a<|F1F2|)
定点F和定直线l,点F不在直线l上,P到l距离为d,|PF|=d
标准方程
焦点在x轴上
+=1(a>b>0)
焦点在x轴上
-=1(a>0,b>0)
焦点在x轴正半轴上y2=2px(p>0)
图象
几何性质
范围
|x|≤a,|y|≤b[来源:]
|x|≥a,y∈R[来源:学#科#网Z#X#X#K][来源:]
x≥0,y∈R
顶点
(±a,0),(0,±b)
(±a,0)
(0,0)
对称性
关于x轴、y轴和原点对称
关于x轴对称
焦点
(±c,0)
轴
长轴长2a,短轴长2b
实轴长2a,虚轴长2b
离心率
e==(0
1)
e=1
准线
x=-
通径
|AB|=
|AB|=2p
渐近线
y=±x
【误区警示】
1.求椭圆、双曲线方程时,注意椭圆中c2=a2+b2,双曲线中c2=a2-b2的区别.
2.注意焦点在x轴上与y轴上的双曲线的渐近线方程的区别.
3.平行于双曲线渐近线的直线与双曲线有且仅有一个交点;平行于抛物线的轴的直线与抛物线有且仅有一个交点.
高频考点一 椭圆的定义及其方程
例1.(2018年天津卷)设椭圆(a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为,点A的坐标为,且.
(I)求椭圆的方程;
(II)设直线l:与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若 (O为原点) ,求k的值.
【答案】(Ⅰ);(Ⅱ)或
【解析】(Ⅰ)设椭圆的焦距为2c,由已知有,
又由a2=b2+c2,可得2a=3b.由已知可得,,,
由,可得ab=6,从而a=3,b=2.
所以,椭圆的方程为.
(Ⅱ)设点P的坐标为(x1,y1),点Q的坐标为(x2,y2).
由已知有y1>y2>0,故.
又因为,而∠OAB=,故.
由,可得5y1=9y2.
由方程组消去x,可得.
易知直线AB的方程为x+y–2=0,
由方程组消去x,可得.
由5y1=9y2,可得5(k+1)=,
两边平方,整理得,
解得,或.
所以,k的值为或
【变式探究】(2017·北京卷)已知椭圆C的两个顶点分别为A(-2,0),B(2,0),焦点在x轴上,离心率为.
(1)求椭圆C的方程;
(2)点D为x轴上一点,过D作x轴的垂线交椭圆C于不同的两点M,N,过D作AM的垂线交BN于点E.求证:△BDE与△BDN的面积之比为4∶5.学=科网
(1)解:设椭圆C的方程为+=1(a>b>0),
由题意得解得c=,
所以b2=a2-c2=1,
所以椭圆C的方程为+y2=1.
(2)设M(m,n),则D(m,0),N(m,-n),
由题设知m≠±2,且n≠0.
直线AM的斜率kAM=,
故直线DE的斜率kDE=-,
所以直线DE的方程为y=-(x-m),
直线BN的方程为y=(x-2).
联立解得点E的纵坐标yE=-.
由点M在椭圆C上,得4-m2=4n2,所以yE=-n.
又S△BDE=|BD|·|yE|=|BD|·|n|,
S△BDN=|BD|·|n|,
所以△BDE与△BDN的面积之比为4∶5.
【变式探究】已知椭圆C1:+y2=1(m>1)与双曲线C2:–y2=1(n>0)的焦点重合,e1,e2分别为C1,C2的离心率,则( )
A.m>n且e1e2>1 B.m>n且e1e2<1 C.m1 D.mb>0)的右焦点为F(3,0),过点F的直线交E于A,B两点.若AB的中点坐标为(1,-1),则E的方程为( )
A.+=1 B.+=1
C.+=1 D.+=1
解析 设A(x1,y1),B(x2,y2),
∵A,B在椭圆上,
∴
①-②,得
+=0,
即=-,
∵AB的中点为(1,-1),
∴y1+y2=-2,x1+x2=2,而=kAB==,∴=.
又∵a2-b2=9,∴a2=18,b2=9.
∴椭圆E的方程为+=1,故选D.
答案 D
高频考点二 椭圆的几何性质
例2.(2018年全国Ⅱ卷理数)已知,是椭圆的左,右焦点,A是C的左顶点,点P在过A且斜率为的直线上,为等腰三角形,,则C的离心率为
A. B. C. D.
【答案】D
【解析】因为为等腰三角形,,所以PF2=F1F2=2c,
由AP斜率为得,,
由正弦定理得,
所以,选D.
【变式探究】已知为坐标原点,是椭圆:的左焦点,分别为的左,右顶点.为上一点,且轴.过点的直线与线段交于点,与轴交于点.若直线经过的中点,则的离心率为( )
(A) (B) (C) (D)
【答案】A
【解析】由题意设直线的方程为,分别令与得,.设OE的中点为N,则,则,即,整理,得,所以椭圆C的离心率,故选A.
【变式探究】已知椭圆C:+=1(a>b>0)的离心率为,点P(0,1)和点A(m,n)(m≠0)都在椭圆C上,直线PA交x轴于点M.
(1)求椭圆C的方程,并求点M的坐标(用m,n表示);
(2)设O为原点,点B与点A关于x轴对称,直线PB交x轴于点N.问:y轴上是否存在点Q,使得∠OQM
=∠ONQ?若存在,求点Q的坐标;若不存在,说明理由.
(2)因为点B与点A关于x轴对称,
所以B(m,-n).
设N(xN,0),则xN=.
“存在点Q(0,yQ)使得∠OQM=∠ONQ”,等价于“存在点Q(0,yQ)使得=”,即yQ满足y=|xM||xN|.
因为xM=,xN=,+n2=1.
所以y=|xM||xN|==2.
所以yQ=或yQ=-.
故在y轴上存在点Q,使得∠OQM=∠ONQ,点Q的坐标为(0,)或
(0,-).
高频考点三 双曲线的定义及标准方程
例3.(2018年天津卷)已知双曲线的离心率为2,过右焦点且垂直于x轴的直线与双曲线交于A,B两点. 设A,B到双曲线的同一条渐近线的距离分别为和,且,则双曲线的方程为
A. B. C. D.
【答案】C
【解析】设双曲线的右焦点坐标为(c>0),则,
由可得:,
不妨设:,
双曲线的一条渐近线方程为:,
据此可得:,,
则,则,
双曲线的离心率:,
据此可得:,则双曲线的方程为.
本题选择C选项.
【变式探究】(2017·全国卷Ⅱ)若双曲线C:-=1(a>0,b>0)的一条渐近线被圆(x-2)2+y2=4所截得的弦长为2,则C的离心率为( )
A.2 B.
C. D.
解析:取渐近线y=x,化成一般式bx-ay=0,圆心(2,0)到直线的距离为=,
又由c2=a2+b2得c2=4a2,e2=4,e=2.
答案:A
【变式探究】已知双曲线(b>0),以原点为圆心,双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A、B、C、D四点,四边形的ABCD的面积为2b,则双曲线的方程为( )
(A)(B)(C)(D)
【答案】D
【解析】根据对称性,不妨设A在第一象限,,∴,
∴,故双曲线的方程为,故选D.
【变式探究】若双曲线E:-=1的左、右焦点分别为F1,F2,点P在双曲线E上,且|PF1|=3,则|PF2|等于( )
A.11 B.9 C.5 D.3
解析 由双曲线定义||PF2|-|PF1||=2a,∵|PF1|=3,∴P在左支上,∵a=3,∴|PF2|-|PF1|=6,∴|PF2|=9,故选B.
答案 B
高频考点四 双曲线的几何性质
例4.(2018年全国I卷理数)已知双曲线C:,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M、N.若OMN为直角三角形,则|MN|=
A. B. 3 C. D. 4
【答案】B
【解析】根据题意,可知其渐近线的斜率为,且右焦点为,
从而得到,所以直线的倾斜角为或,
根据双曲线的对称性,设其倾斜角为,
可以得出直线的方程为,
分别与两条渐近线和联立,
求得,
所以,故选B.
【变式探究】已知方程表示双曲线,且该双曲线两焦点间的距离为4,则n
的取值范围是( )
(A) (B) (C) (D)
【答案】A
【解析】由题意知:双曲线的焦点在轴上,所以,解得,因为方程表示双曲线,所以,解得,所以的取值范围是,故选A.
【变式探究】已知A,B为双曲线E的左,右顶点,点M在E上,△ABM为等腰三角形,且顶角为120°,则E的离心率为( )学科=网
A. B.2 C. D.
解析 如图,设双曲线E的方程为-=1(a>0,b>0),则|AB|=2a,由双曲线的对称性,可设点M(x1,y1)在第一象限内,过M作MN⊥x轴于点N(x1,0),∵△ABM为等腰三角形,且∠ABM=120°,∴|BM|=|AB|=2a,∠MBN=60°,∴y1=|MN|=|BM|sin∠MBN=2asin 60°=a,x1=|OB|+|BN|=a+2acos 60°=2a.将点M(x1,y1)的坐标代入-=1,可得a2=b2,∴e===,选D.
答案 D
高频考点五 抛物线的定义及方程
例5.(2018年全国I卷理数)设抛物线C:y2=4x的焦点为F,过点(–2,0)且斜率为的直线与C交于M,N两点,则=
A. 5 B. 6 C. 7 D. 8
【答案】D
【解析】根据题意,过点(–2,0)且斜率为的直线方程为,与抛物线方程联立,消元整理得:,解得,又,所以,从而可以求得,故选D.
【变式探究】(2017·全国卷Ⅱ)过抛物线C:y2=4x的焦点F,且斜率为的直线交C于点M(M在x轴的上方),l为C的准线,点N在l上且MN⊥l,则M到直线NF的距离为( )
A. B.2
C.2 D.3
【变式探究】设O为坐标原点,P是以F为焦点的抛物线上任意一点,M是线段PF上的点,且=2,则直线OM的斜率的最大值为( )
(A) (B) (C) (D)1
【答案】C
【解析】设(不妨设),则
,故选C.
【变式探究】过抛物线y2=4x的焦点F的直线交该抛物线于A,B两点,O为坐标原点,若|AF|=3,则△AOB的面积为( )
A. B. C. D.2
解析 设点A(x1,y1),B(x2,y2),
由|AF|=3及抛物线定义可得,x1+1=3,∴x1=2.
∴A点坐标为(2,2),则直线AB的斜率
k==2.
∴直线AB的方程为y=2(x-1),
即为2x-y-2=0,
则点O到该直线的距离为d=.
由
消去y得,2x2-5x+2=0,
解得x1=2,x2=.∴|BF|=x2+1=,
∴|AB|=3+=.∴S△AOB=|AB|·d
=××=.学-科网
答案 C
高频考点六 抛物线的几何性质
例6.(2018年浙江卷)如图,已知点P是y轴左侧(不含y轴)一点,抛物线C:y2=4x上存在不同的两点A,B满足PA,PB的中点均在C上.
(Ⅰ)设AB中点为M,证明:PM垂直于y轴;
(Ⅱ)若P是半椭圆x2+=1(x<0)上的动点,求△PAB面积的取值范围.
【答案】(Ⅰ)见解析
(Ⅱ)
【解析】(Ⅰ)设,,.
因为,的中点在抛物线上,所以,为方程
即的两个不同的实数根.
所以.
因此,垂直于轴.
(Ⅱ)由(Ⅰ)可知
所以,.
因此,的面积.
因为,所以.
因此,面积的取值范围是.
【变式探究】(2017·全国卷Ⅲ)已知抛物线C:y2=2x,过点(2,0)的直线l交C于A,B两点,圆M是以线段AB为直径的圆.
(1)证明:坐标原点O在圆M上;
(2)设圆M过点P(4,-2),求直线l与圆M的方程.
(1)证明:设l:x=my+2,A(x1,y1),B(x2,y2),
联立得y2-2my-4=0,
Δ=4m2+16恒大于0,y1+y2=2m,y1y2=-4.
·=x1x2+y1y2
=(my1+2)(my2+2)+y1y2
=(m2+1)y1y2+2m(y1+y2)+4
=-4(m2+1)+2m·2m+4=0,
所以⊥,即O在圆M上.
(2)解:由(1)可得y1+y2=2m,x1+x2=m(y1+y2)+4=2m2+4.
故圆心M的坐标为(m2+2,m),圆M的半径r=.
由于圆M过点P(4,-2),因此·=0,故(x1-4)·(x2-4)+(y1+2)·(y2+2)=0,
即x1x2-4(x1+x2)+y1y2+2(y1+y2)+20=0.
由(1)可得y1y2=-4,x1x2=4,
所以2m2-m-1=0,解得m=1或m=-.
当m=1时,直线l的方程为x-y-2=0,圆心M的坐标为(3,1),圆M的半径为,圆M的方程为(x-3)2+(y-1)2=10.
当m=-时,直线l的方程为2x+y-4=0,圆心M的坐标为,
圆M的半径为,圆M的方程为+=.
【变式探究】以抛物线C的顶点为圆心的圆交C于A、B两点,交C的准线于D、E两点.已知|AB|=,|DE|=,则C的焦点到准线的距离为
(A)2 (B)4 (C)6 (D)8
【答案】B
【解析】如图,设抛物线方程为,交轴于点,则,即点纵坐标为,则点横坐标为,即,由勾股定理知, ,即,解得,即的焦点到准线的距离为4,故选B.
【变式探究】已知双曲线-=1(a>0,b>0)的一条渐近线过点(2,) ,且双曲线的一个焦点在抛物线y2=4x的准线上,则双曲线的方程为( )
A.-=1 B.-=1
C.-=1 D.-=1
解析 双曲线-=1的渐近线方程为y=±x,又渐近线过点(2,),所以=,即2b=a,①
抛物线y2=4x的准线方程为x=-,由已知,得=,即a2+b2=7②,
联立①②解得a2=4,b2=3,所求双曲线的方程为-=1,选D.
答案 D
1. (2018年浙江卷)双曲线的焦点坐标是
A. (−,0),(,0) B. (−2,0),(2,0)
C. (0,−),(0,) D. (0,−2),(0,2)
【答案】B
【解析】因为双曲线方程为,所以焦点坐标可设为,
因为,所以焦点坐标为,选B.
2. (2018年天津卷)已知双曲线的离心率为2,过右焦点且垂直于x轴的直线与双曲线交于A,B两点. 设A,B到双曲线的同一条渐近线的距离分别为和,且,则双曲线的方程为
A. B. C. D.
【答案】C
【解析】设双曲线的右焦点坐标为(c>0),则,
由可得:,
不妨设:,
双曲线的一条渐近线方程为:,
据此可得:,,
则,则,
双曲线的离心率:,
据此可得:,则双曲线的方程为.
本题选择C选项.
3. (2018年全国I卷理数)已知双曲线C:,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M、N.若OMN为直角三角形,则|MN|=
A. B. 3 C. D. 4
【答案】B
【解析】根据题意,可知其渐近线的斜率为,且右焦点为,
从而得到,所以直线的倾斜角为或,
根据双曲线的对称性,设其倾斜角为,
可以得出直线的方程为,
分别与两条渐近线和联立,
求得,
所以,故选B.
4. (2018年全国Ⅲ卷理数)设是双曲线()的左、右焦点,是坐标原点.过作的一条渐近线的垂线,垂足为.若,则的离心率为
A. B. 2 C. D.
【答案】C
5. (2018年全国Ⅱ卷理数)双曲线的离心率为,则其渐近线方程为
A. B. C. D.
【答案】A
【解析】因为渐近线方程为,所以渐近线方程为,选A.
6. (2018年江苏卷)在平面直角坐标系中,若双曲线的右焦点到一条渐近线的距离为,则其离心率的值是________.
【答案】2
【解析】先确定双曲线的焦点到渐近线的距离,再根据条件求离心率。因为双曲线的焦点到渐近线即的距离为所以,因此
7. (2018年全国Ⅱ卷理数)已知,是椭圆的左,右焦点,A是C的左顶点,点P在过A且斜率为的直线上,为等腰三角形,,则C的离心率为
A. B. C. D.
【答案】D
【解析】因为为等腰三角形,,所以PF2=F1F2=2c,
由AP斜率为得,,
由正弦定理得,
所以,选D.
8. (2018年浙江卷)已知点P(0,1),椭圆+y2=m(m>1)上两点A,B满足=2,则当m=___________时,点B横坐标的绝对值最大.
【答案】5
【解析】设,由得
因为A,B在椭圆上,所以
,
与对应相减得,当且仅当时取最大值.
9. (2018年北京卷)已知椭圆,双曲线.若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点,则椭圆M的离心率为__________;双曲线N的离心率为__________.
【答案】 (1). (2). 2
【解析】由正六边形性质得椭圆上一点到两焦点距离之和为,再根据椭圆定义得,所以椭圆M的离心率为
双曲线N的渐近线方程为,由题意得双曲线N的一条渐近线的倾斜角为,
10. (2018年天津卷)设椭圆(a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为,点A的坐标为,且.
(I)求椭圆的方程;
(II)设直线l:与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若 (O为原点) ,求k的值.
【答案】(Ⅰ);(Ⅱ)或
【解析】(Ⅰ)设椭圆的焦距为2c,由已知有,
又由a2=b2+c2,可得2a=3b.由已知可得,,,
由,可得ab=6,从而a=3,b=2.
所以,椭圆的方程为.
(Ⅱ)设点P的坐标为(x1,y1),点Q的坐标为(x2,y2).
由已知有y1>y2>0,故.
又因为,而∠OAB=,故.
由,可得5y1=9y2.
由方程组消去x,可得.
易知直线AB的方程为x+y–2=0,
由方程组消去x,可得.
由5y1=9y2,可得5(k+1)=,
两边平方,整理得,
解得,或.
所以,k的值为或
11. (2018年江苏卷)如图,在平面直角坐标系中,椭圆C过点,焦点,圆O的直径为.
(1)求椭圆C及圆O的方程;
(2)设直线l与圆O相切于第一象限内的点P.
①若直线l与椭圆C有且只有一个公共点,求点P的坐标;
②直线l与椭圆C交于两点.若的面积为,求直线l的方程.
【答案】(1)椭圆C的方程为;圆O的方程为
(2)①点P的坐标为;②直线l的方程为
(2)①设直线l与圆O相切于,则,
所以直线l的方程为,即.
由,消去y,得
.(*)
因为直线l与椭圆C有且只有一个公共点,
所以.
因为,所以.
因此,点P的坐标为.
②因为三角形OAB的面积为,所以,从而.
设,
由(*)得,
所以
.
因为,
所以,即,
解得舍去),则,因此P的坐标为.
综上,直线l的方程为.
12. (2018年全国I卷理数)设椭圆的右焦点为,过的直线与交于两点,点的坐标为.
(1)当与轴垂直时,求直线的方程;
(2)设为坐标原点,证明:.
【答案】(1) AM的方程为或.
(2)证明见解析.
【解析】
(1)由已知得,l的方程为x=1.
由已知可得,点A的坐标为或.
所以AM的方程为或.
(2)当l与x轴重合时,.
当l与x轴垂直时,OM为AB的垂直平分线,所以.
当l与x轴不重合也不垂直时,设l的方程为,,
则,直线MA,MB的斜率之和为.
由得
.
将代入得
.
所以,.
则.
从而,故MA,MB的倾斜角互补,所以.
综上,.
13. (2018年全国Ⅲ卷理数)已知斜率为的直线与椭圆交于,两点,线段的中点为.
(1)证明:;
(2)设为的右焦点,为上一点,且.证明:,,成等差数列,并求该数列的公差.
【答案】(1)
(2)或
【解析】(1)设,则.
两式相减,并由得
.
由题设知,于是
.①
由题设得,故.
(2)由题意得,设,则
.
由(1)及题设得.
又点P在C上,所以,从而,.
于是
.
同理.
所以.
故,即成等差数列.
设该数列的公差为d,则
.②
将代入①得.
所以l的方程为,代入C的方程,并整理得.
故,代入②解得.
所以该数列的公差为或.
14. (2018年全国I卷理数)设抛物线C:y2=4x的焦点为F,过点(–2,0)且斜率为的直线与C交于M,N两点,则=
A. 5 B. 6 C. 7 D. 8
【答案】D
【解析】根据题意,过点(–2,0)且斜率为的直线方程为,与抛物线方程联立,消元整理得:,解得,又,所以,从而可以求得,故选D.
15. (2018年全国Ⅲ卷理数)已知点和抛物线,过的焦点且斜率为的直线与交于,两点.若,则________.
【答案】2
【解析】设
则
所以
所以
取AB中点,分别过点A,B作准线的垂线,垂足分别为
因为,
因为M’为AB中点,
所以MM’平行于x轴
因为M(-1,1)
所以,则即
故答案为2.
16. (2018年浙江卷)如图,已知点P是y轴左侧(不含y轴)一点,抛物线C:y2=4x上存在不同的两点A,B满足PA,PB的中点均在C上.
(Ⅰ)设AB中点为M,证明:PM垂直于y轴;
(Ⅱ)若P是半椭圆x2+=1(x<0)上的动点,求△PAB面积的取值范围.
【答案】(Ⅰ)见解析
(Ⅱ)
【解析】(Ⅰ)设,,.
因为,的中点在抛物线上,所以,为方程
即的两个不同的实数根.
所以.
因此,垂直于轴.
(Ⅱ)由(Ⅰ)可知
所以,.
因此,的面积.
因为,所以.
因此,面积的取值范围是.
17. (2018年北京卷)已知抛物线C:=2px经过点(1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(Ⅰ)求直线l的斜率的取值范围;
(Ⅱ)设O为原点,,,求证:为定值.
【答案】(1) 取值范围是(-∞,-3)∪(-3,0)∪(0,1)
(2)证明过程见解析
【解析】(Ⅰ)因为抛物线y2=2px经过点P(1,2),
所以4=2p,解得p=2,所以抛物线的方程为y2=4x.
由题意可知直线l的斜率存在且不为0,
设直线l的方程为y=kx+1(k≠0).
由得.
依题意,解得k<0或00).
设A(x1,y1),B(x2,y2).
由得.
,故.
所以.
由题设知,解得k=–1(舍去),k=1.
因此l的方程为y=x–1.
(2)由(1)得AB的中点坐标为(3,2),所以AB的垂直平分线方程为
,即.
设所求圆的圆心坐标为(x0,y0),则
解得或
因此所求圆的方程为
或.
1.【2017课标1,理10】已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A、B两点,直线l2与C交于D、E两点,则|AB|+|DE|的最小值为
A.16 B.14 C.12 D.10
【答案】A
【解析】设,直线的方程为,联立方程,得,∴,同理直线与抛物线的交点满足,由抛物线定义可知
,当且仅当(或)时,取等号.
2.【2017课标II,理9】若双曲线(,)的一条渐近线被圆所截得的弦长为2,则的离心率为( )
A.2 B. C. D.
【答案】A
【解析】由几何关系可得,双曲线的渐近线方程为,圆心到渐近线距离为,则点到直线的距离为,
即,整理可得,双曲线的离心率.故选A.
3.【2017浙江,2】椭圆的离心率是
A. B. C. D.
【答案】B
【解析】,选B.
4.【2017天津,理5】已知双曲线的左焦点为,离心率为.若经过和两点的直线平行于双曲线的一条渐近线,则双曲线的方程为
(A) (B)(C)(D)
【答案】B
【解析】由题意得,选B.
5.【2017北京,理9】若双曲线的离心率为,则实数m=_________.
【答案】2
【解析】,所以,解得 .
6.【2017课标1,理】已知双曲线C:(a>0,b>0)的右顶点为A,以A为圆心,b为半径作圆A,圆A与双曲线C的一条渐近线交于M、N两点.若∠MAN=60°,则C的离心率为________.
【答案】
【解析】如图所示,作,因为圆A与双曲线C的一条渐近线交于M、N两点,则为双曲线的渐近线上的点,且,,
而,所以,
点到直线的距离,
在中,,代入计算得,即,
由得,
所以.
7.【2017课标II,理16】已知是抛物线的焦点,是上一点,的延长线交轴于点。若为的中点,则 。
【答案】6
【解析】如图所示,不妨设点M位于第一象限,设抛物线的准线与轴交于点,作与点,与点,由抛物线的解析式可得准线方程为,则,在直角梯形中,中位线,由抛物线的定义有:,结合题意,有,故.
8.【2017课标3,理5】已知双曲线C: (a>0,b>0)的一条渐近线方程为,且与椭圆有公共焦点,则C的方程为
A. B. C. D.
【答案】B
【解析】双曲线C: (a>0,b>0)的渐近线方程为 ,
椭圆中: ,椭圆,即双曲线的焦点为 ,
据此可得双曲线中的方程组: ,解得: ,
则双曲线 的方程为 .
故选B.
9.【2017山东,理14】在平面直角坐标系中,双曲线的右支与焦点为的抛物线交于两点,若,则该双曲线的渐近线方程为 .
【答案】
10.【2017课标1,理20】已知椭圆C:(a>b>0),四点P1(1,1),P2(0,1),P3(–1,),P4(1,)中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.
【答案】(1).(2)见解析。
【解析】(1)由于, 两点关于y轴对称,故由题设知C经过, 两点.
又由知,C不经过点P1,所以点P2在C上.
因此,解得.
故C的方程为.
(2)设直线P2A与直线P2B的斜率分别为k1,k2,
如果l与x轴垂直,设l:x=t,由题设知,且,可得A,B的坐标分别为(t, ),(t, ).
则,得,不符合题设.
从而可设l: ().将代入得
由题设可知.
设A(x1,y1),B(x2,y2),则x1+x2=,x1x2=.
而
.
由题设,故.
即.
解得.
当且仅当时, ,欲使l:,即,
所以l过定点(2, )
11.【2017课标II,理】设O为坐标原点,动点M在椭圆C:上,过M作x轴的垂线,垂足为N,点P满足。
(1) 求点P的轨迹方程;
(2)设点Q在直线上,且。证明:过点P且垂直于OQ的直线l过C的左焦点F。
【答案】(1) 。(2)证明略。
【解析】(1)设P(x,y),M(),则N(),
由得.
因为M()在C上,所以.
因此点P的轨迹为.
由题意知F(-1,0),设Q(-3,t),P(m,n),则
,
.
由得-3m-+tn-=1, 又由(1)知,故
3+3m-tn=0.
所以,即.又过点P存在唯一直线垂直于OQ,所以过点P且垂直于OQ的直线l过C的左焦点F.
12.【2017山东,理21】在平面直角坐标系中,椭圆:的离心率为,焦距为.
(Ⅰ)求椭圆的方程;
(Ⅱ)如图,动直线:交椭圆于两点,是椭圆上一点,直线的斜率为,且,是线段延长线上一点,且,的半径为,是的两条切线,切点分别为.求的最大值,并求取得最大值时直线的斜率.
【答案】(I).
(Ⅱ)的最大值为,取得最大值时直线的斜率为.
【解析】
(I)由题意知 , ,
所以,
因此 椭圆的方程为.
(Ⅱ)设,
联立方程
得,
由题意知,
且,
所以.
由题意可知圆的半径为
由题设知,
所以
因此直线的方程为.
联立方程
得,
因此.
由题意可知,
而
,
令,
则,
因此,
当且仅当,即时等号成立,此时,
所以,
因此,
所以 最大值为.
综上所述: 的最大值为,取得最大值时直线的斜率为.
13.【2017北京,理18】已知抛物线C:y2=2px过点P(1,1).过点(0,)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点.
(Ⅰ)求抛物线C的方程,并求其焦点坐标和准线方程;
(Ⅱ)求证:A为线段BM的中点.学科=网
【答案】(Ⅰ)方程为,抛物线C的焦点坐标为(,0),准线方程为.(Ⅱ)详见解析.
【解析】
(Ⅰ)由抛物线C: 过点P(1,1),得.
所以抛物线C的方程为.
抛物线C的焦点坐标为(,0),准线方程为.
(Ⅱ)由题意,设直线l的方程为(),l与抛物线C的交点为, .
由,得.
则, .
因为点P的坐标为(1,1),所以直线OP的方程为,点A的坐标为.
直线ON的方程为,点B的坐标为.
因为
,
所以.
故A为线段BM的中点.
14.【2017天津,理19】设椭圆的左焦点为,右顶点为,离心率为.已知是抛物线的焦点,到抛物线的准线的距离为.
(I)求椭圆的方程和抛物线的方程;
(II)设上两点,关于轴对称,直线与椭圆相交于点(异于点),直线与轴相交于点.若的面积为,求直线的方程.
【答案】(Ⅰ), .(Ⅱ),或.
【解析】
(Ⅰ)解:设的坐标为.依题意, , , ,解得, , ,于是.所以,椭圆的方程为,抛物线的方程为.
(Ⅱ)解:设直线的方程为,与直线的方程联立,可得点,故.将与联立,消去,整理得,解得,或.由点异于点,可得点.由,可学*科.网得直线的方程为,令,解得,故.所以.又因为的面积为,故,整理得,解得,所以.
所以,直线的方程为,或.
15.【2017江苏,8】 在平面直角坐标系中,双曲线的右准线与它的两条渐近线分别交于点,,其焦点是,则四边形的面积是 ▲ .
【答案】
【解析】右准线方程为,渐近线方程为,设,则,, ,则.
16.【2017江苏,17】 如图,在平面直角坐标系中,椭圆的左、右焦点分别为, ,离心率为,两准线之间的距离为8.点在椭圆上,且位于第一象限,过点作 直线的垂线,过点作直线的垂线.
(1)求椭圆的标准方程;
(2)若直线的交点在椭圆上,求点的坐标.
【答案】(1)(2)
【解析】(1)设椭圆的半焦距为c.
因为椭圆E的离心率为,两准线之间的距离为8,所以, ,
解得,于是,
因此椭圆E的标准方程是.
(2)由(1)知, , .
设,因为点为第一象限的点,故.
当时, 与相交于,与题设不符.
当时,直线的斜率为,直线的斜率为.
因为, ,所以直线的斜率为,直线的斜率为,
从而直线的方程:, ①
直线的方程:. ②
由①②,解得,所以.
因为点在椭圆上,由对称性,得,即或.
又在椭圆E上,故.
由,解得;,无解.
因此点P的坐标为.
1. 【2016高考新课标1卷】已知方程表示双曲线,且该双曲线两焦点间的距离为4,则n的取值范围是( )
(A) (B) (C) (D)
【答案】A
【解析】由题意知:双曲线的焦点在轴上,所以,解得,因为方程表示双曲线,所以,解得,所以的取值范围是,故选A.
2.【2016年高考四川理数】设O为坐标原点,P是以F为焦点的抛物线上任意一点,M是线段PF上的点,且=2,则直线OM的斜率的最大值为( )
(A) (B) (C) (D)1
【答案】C
【解析】设(不妨设),则
,故选C.
3.【2016高考新课标2理数】已知是双曲线的左,右焦点,点在上,与轴垂直,,则的离心率为( )
(A) (B) (C) (D)2
【答案】A
【解析】因为垂直于轴,所以,因为,即,化简得,故双曲线离心率.选A.
4.【2016高考浙江理数】已知椭圆C1:+y2=1(m>1)与双曲线C2:–y2=1(n>0)的焦点重合,e1,e2分别为C1,C2的离心率,则( )
A.m>n且e1e2>1 B.m>n且e1e2<1 C.m1 D.m0),以原点为圆心,双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A、B、C、D四点,四边形的ABCD的面积为2b,则双曲线的方程为( )
(A)(B)(C)(D)
【答案】D
【解析】根据对称性,不妨设A在第一象限,,∴,
∴,故双曲线的方程为,故选D.
9.【2016高考江苏卷】如图,在平面直角坐标系中,是椭圆的右焦点,直线 与椭圆交于两点,且,则该椭圆的离心率是 ▲ .
【答案】
【解析】由题意得,因此
10.【2016高考天津理数】设抛物线,(t为参数,p>0)的焦点为F,准线为l.过抛物线上一点A作l的垂线,垂足为B.设C(p,0),AF与BC相交于点E.若|CF|=2|AF|,且△ACE的面积为,则p的值为_________.
【答案】
【解析】抛物线的普通方程为,,,
又,则,由抛物线的定义得,所以,则,
由得,即,
所以,,
所以,解得.
11.【2016高考山东理数】已知双曲线E: (a>0,b>0),若矩形ABCD的四个顶点在E上,AB,CD的中点为E的两个焦点,且2|AB|=3|BC|,则E的离心率是_______.
【答案】2
【解析】假设点A在第一象限,点B在第二象限,则,,所以,,由,得离心率或(舍去),所以E的离心率为2.
12.【2016年高考北京理数】双曲线(,)的渐近线为正方形OABC的边OA,OC所在的直线,点B为该双曲线的焦点,若正方形OABC的边长为2,则_______________.
【答案】2
【解析】∵是正方形,∴,即直线方程为,此为双曲线的渐近线,因此,又由题意,∴,.故填:2.
13.【2016高考江苏卷】在平面直角坐标系xOy中,双曲线的焦距是________▲________.
【答案】
【解析】.焦距为2c[来源
故答案应填:。
14.【2016高考山东理数】(本小题满分14分)
平面直角坐标系中,椭圆C: 的离心率是,抛物线E:的焦点F是C的一个顶点.
(I)求椭圆C的方程;
(II)设P是E上的动点,且位于第一象限,E在点P处的切线与C交与不同的两点A,B,线段AB的中点为D,直线OD与过P且垂直于x轴的直线交于点M.
(i)求证:点M在定直线上;
(ii)直线与y轴交于点G,记的面积为,的面积为,求 的最大值及取得最大值时点P的坐标.
【答案】(Ⅰ);(Ⅱ)(i)见解析;(ii)的最大值为,此时点的坐标为
【解析】
(Ⅰ)由题意知,可得:.
因为抛物线的焦点为,所以,
所以椭圆C的方程为.
(Ⅱ)(Ⅰ)设,由可得,
所以直线的斜率为,
因此直线的方程为,即.
设,联立方程
得,
由,得且,
因此,
将其代入得,
因为,所以直线方程为.
联立方程,得点的纵坐标为,
即点在定直线上.
(Ⅱ)由(Ⅰ)知直线方程为,
令得,所以,
又,
所以,
,
所以,
令,则,
当,即时,取得最大值,此时,满足,
所以点的坐标为,因此的最大值为,此时点的坐标为.
15.【2016高考江苏卷】(本小题满分10分)
如图,在平面直角坐标系xOy中,已知直线,抛物线
(1)若直线l过抛物线C的焦点,求抛物线C的方程;
(2)已知抛物线C上存在关于直线l对称的相异两点P和Q.
①求证:线段PQ的中点坐标为;
②求p的取值范围.
【答案】(1)(2)①详见解析,②
【解析】
解:(1)抛物线的焦点为
由点在直线上,得,即
所以抛物线C的方程为
(2)设,线段PQ的中点
因为点P和Q关于直线对称,所以直线垂直平分线段PQ,
于是直线PQ的斜率为,则可设其方程为
①由消去得
因为P 和Q是抛物线C上的相异两点,所以
从而,化简得.
方程(*)的两根为,从而
因为在直线上,所以
因此,线段PQ的中点坐标为
②因为在直线上
所以,即
由①知,于是,所以
因此的取值范围为
16.【2016高考天津理数】(本小题满分14分)
设椭圆()的右焦点为,右顶点为,已知,其中 为原点,为椭圆的离心率.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过点的直线与椭圆交于点(不在轴上),垂直于的直线与交于点,与轴交于点,若,且,求直线的斜率的取值范围.
【答案】(Ⅰ)(Ⅱ)
【解析】(Ⅰ)解:设,由,即,可得,又,所以,因此,所以椭圆的方程为.
(Ⅱ)解:设直线的斜率为(),则直线的方程为.
设,由方程组,消去,整理得.
解得,或,由题意得,从而.
由(Ⅰ)知,,设,有,.
由,得,所以,解得.
因此直线的方程为.
设,由方程组消去,解得.
在中,,即,
化简得,即,解得或.
所以,直线的斜率的取值范围为.
17.【2016高考新课标3理数】已知抛物线:的焦点为,平行于轴的两条直线分别交于两点,交的准线于两点.
(I)若在线段上,是的中点,证明;
(II)若的面积是的面积的两倍,求中点的轨迹方程.
【答案】(Ⅰ)见解析;(Ⅱ).
【解析】由题设.设,则,且
.
记过两点的直线为,则的方程为. .....3分
(Ⅰ)由于在线段上,故.
记的斜率为,的斜率为,则,
所以. ......5分
(Ⅱ)设与轴的交点为,
则.
由题设可得,所以(舍去),.
设满足条件的的中点为.
当与轴不垂直时,由可得.
而,所以.
当与轴垂直时,与重合,所以,所求轨迹方程为. ....12分[来源:Z#xx#k.Com]
18.【2016高考浙江理数】(本题满分15分)如图,设椭圆(a>1).
(I)求直线y=kx+1被椭圆截得的线段长(用a、k表示);
(II)若任意以点A(0,1)为圆心的圆与椭圆至多有3个公共点,求椭圆离心率的取值
范围.
【答案】(I);(II).
【解析】
(Ⅰ)设直线被椭圆截得的线段为,由得,
故,.
因此.
(Ⅱ)假设圆与椭圆的公共点有个,由对称性可设轴左侧的椭圆上有两个不同的点,,满足
.
记直线,的斜率分别为,,且,,.
由(Ⅰ)知,,,
故,
所以.
由于,,得,
因此, ①
因为①式关于,的方程有解的充要条件是,
所以.
因此,任意以点为圆心的圆与椭圆至多有个公共点的充要条件为,
由得,所求离心率的取值范围为.
19.【2016高考新课标2理数】已知椭圆的焦点在轴上,是的左顶点,斜率为的直线交于两点,点在上,.
(Ⅰ)当时,求的面积;
(Ⅱ)当时,求的取值范围.
【答案】(Ⅰ);(Ⅱ).
【解析】(Ⅰ)设,则由题意知,当时,的方程为,.
由已知及椭圆的对称性知,直线的倾斜角为.因此直线的方程为.
将代入得.解得或,所以.
因此的面积.
(Ⅱ)由题意,,.
将直线的方程代入得.
由得,故.
由题设,直线的方程为,故同理可得,
由得,即.
当时上式不成立,
因此.等价于,
即.由此得,或,解得.
因此的取值范围是.
20.【2016年高考北京理数】(本小题14分)
已知椭圆C: ()的离心率为 ,,,,的面积为1.
(1)求椭圆C的方程;
(2)设的椭圆上一点,直线与轴交于点M,直线PB与轴交于点N.
求证:为定值.
【答案】(1);(2)详见解析.
【解析】
(Ⅰ)由题意得解得.
所以椭圆的方程为.
(Ⅱ)由(Ⅰ)知,,
设,则.
当时,直线的方程为.
令,得,从而.
直线的方程为.
令,得,从而.
所以
.
当时,,
所以.
综上,为定值.
21.【2016年高考四川理数】(本小题满分13分)
已知椭圆E:的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线与椭圆E有且只有一个公共点T.
(Ⅰ)求椭圆E的方程及点T的坐标;学——科网
(Ⅱ)设O是坐标原点,直线l’平行于OT,与椭圆E交于不同的两点A、B,且与直线l交于点P.证明:存在常数,使得,并求的值.
【答案】(Ⅰ),点T坐标为(2,1);(Ⅱ).
【解析】(I)由已知,,即,所以,则椭圆E的方程为.
由方程组得.①
方程①的判别式为,由,得,
此方程①的解为,
所以椭圆E的方程为.
点T坐标为(2,1).
(II)由已知可设直线 的方程为,
有方程组可得
所以P点坐标为(),.
设点A,B的坐标分别为.
由方程组可得.②
方程②的判别式为,由,解得.
由②得.
所以,
同理,
所以
.
故存在常数,使得.
22. 【2016高考上海理数】(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
双曲线的左、右焦点分别为,直线过且与双曲线交于两点。
(1)若的倾斜角为,是等边三角形,求双曲线的渐近线方程;
(2)设,若的斜率存在,且,求的斜率.
【答案】(1).(2).
【解析】
(1)设.
由题意,,,,
因为是等边三角形,所以,
即,解得.
故双曲线的渐近线方程为.
(2)由已知,,.
设,,直线.显然.
由,得.
因为与双曲线交于两点,所以,且.
设的中点为.
由即,知,故.
而,,,
所以,得,故的斜率为.
1.(2015·陕西,20)已知椭圆E:+=1(a>b>0)的半焦距为c,原点O到经过两点(c,0),(0,b)的直线的距离为c.
(1)求椭圆E的离心率;
(2)如图,AB是圆M:(x+2)2+(y-1)2=的一条直径,若椭圆E经过A,B两点,求椭圆E的方程.
解 (1)过点(c,0),(0,b)的直线方程为bx+cy-bc=0,
则原点O到该直线的距离d==,
由d=c,得a=2b=2,解得离心率=.
(2)法一 由(1)知,椭圆E的方程为x2+4y2=4b2.①
依题意,圆心M(-2,1)是线段AB的中点,且|AB|=,
易知,AB与x轴不垂直,设其方程为y=k(x+2)+1,代入①得(1+4k2)x2+8k(2k+1)x+4(2k+1)2-4b2=0,
设A(x1,y1),B(x2,y2),则x1+x2=-,x1x2=,
由x1+x2=-4,得-=-4,解得k=,
从而x1x2=8-2b2,
于是|AB|=|x1-x2|
==,
由|AB|=,得=,
解得b2=3,
故椭圆E的方程为+=1.
法二 由(1)知,椭圆E的方程为x2+4y2=4b2,②
依题意,点A,B关于圆心M(-2,1)对称,且|AB|=,
设A(x1,y1),B(x2,y2),则x+4y=4b2,x+4y=4b2,
两式相减并结合x1+x2=-4,y1+y2=2,得-4(x1-x2)+8(y1-y2)=0,
易知AB与x轴不垂直,则x1≠x2,
所以AB的斜率kAB==,
因此直线AB的方程为y=(x+2)+1,代入②得x2+4x+8-2b2=0,
所以x1+x2=-4,x1x2=8-2b2,
于是|AB|=|x1-x2|
==.
由|AB|=,得=,解得b2=3,
故椭圆E的方程为+=1.
2.(2015·广东,7)已知双曲线C:-=1的离心率e=,且其右焦点为F2(5,0),则双曲线C的方程为( )
A.-=1 B.-=1
C.-=1 D.-=1
解析 因为所求双曲线的右焦点为F2(5,0)且离心率为e==,所以c=5,a=4,b2=c2-a2=9,所以所求双曲线方程为-=1,故选B.
答案 B
3.(2015·新课标全国Ⅰ,5)已知M(x0,y0)是双曲线C:-y2=1上的一点,F1,F2是C的两个焦点,若·<0,则y0的取值范围是( )
A. B.
C. D.
解析 由题意知M在双曲线C:-y2=1上,又在x2+y2=3内部,由得y=±,所以-0)交于M,N两点,
(1)当k=0时,分别求C在点M和N处的切线方程;
(2)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由.
解 (1)由题设可得M(2,a),N(-2,a),
或M(-2,a),N(2,a).
又y′=,故y=在x=2处的导数值为,C在点(2,a)处的切线方程为y-a=(x-2),即x-y-a=0.
y=在x=-2处的导数值为-,C在点(-2,a)处的切线方程为y-a=-(x+2),
即x+y+a=0.
故所求切线方程为x-y-a=0和x+y+a=0.
1. 【2014高考福建卷第9题】设分别为和椭圆上的点,则两点间的最大距离是( )
A. B. C. D.
【答案】D
【解析】依题意两点间的最大距离可以转化为圆心到椭圆上的点的最大距离再加上;圆的半径.设.圆心到椭圆的最大距离.所以两点间的最大距离是.故选D.
2. 【2014高考广东卷理第4题】若实数满足,则曲线与曲线的( )
A.离心率相等 B.虚半轴长相等 C.实半轴长相等 D.焦距相等
【答案】D
【解析】,则,,
双曲线的实半轴长为,虚半轴长为,焦距为
,离心率为,双曲线的实半轴长为,虚半轴长为,焦距为,离心率为,因此,两双曲线的焦距相等,故选D.
【考点定位】双曲线
3. 【2014高考湖北卷理第9题】已知是椭圆和双曲线的公共焦点,是他们的一个公共点,且,则椭圆和双曲线的离心率的倒数之和的最大值为( )
A. B. C.3 D.2
【答案】A
【解析】设椭圆方程为,双曲线方程为(),半焦距为,由面积公式得,所以,
令,,为参数,
所以.
所以椭圆和双曲线的离心率的倒数之和的最大值为,故选A.
【考点定位】椭圆、双曲线
4. 【2014高考湖南卷第15题】如图4,正方形和正方形的边长分别为,原点为的中点,抛物线经过两点,则.
【答案】
【解析】由题可得,因为在抛物线上,
所以,故填.
【考点定位】抛物线
5. 【2014江西高考理第16题】过点作斜率为的直线与椭圆:相交于,若是线段的中点,则椭圆的离心率为 .
【答案】
【解析】设,则由两式相减变形得:即,从而
【考点定位】椭圆
6. 【2014辽宁高考理第10题】已知点在抛物线C:的准线上,过点A的直线与C在第一象限相切于点B,记C的焦点为F,则直线BF的斜率为( )
A. B. C. D.
【答案】D
【解析】由于点在抛物线C:的准线上,所以,设直线AB
的方程为,将与联立,即,则(负值舍去),将k=2代入得y=8,即可求出x=8,故B(8,8),所以,故选D.
【考点定位】抛物线
7. 【2014辽宁高考理第15题】已知椭圆C:,点M与C的焦点不重合,若M关于C的焦点的对称点分别为A,B,线段MN的中点在C上,则 .
【答案】12
【解析】设M,N的中点坐标为P,,则
;由于
,化简可得
,根据椭圆的定义
==6,所以12.
【考点定位】椭圆
8. 【2014全国1高考理第4题】已知为双曲线:的一个焦点,则点到的一条渐近线的距离为( )
A. B. 3 C. D.
【答案】A
【解析】 由已知得,双曲线C的标准方程为.则,,设一个焦点
,一条渐近线的方程为,即,所以焦点F到渐近线的距离为,选A.
【考点定位】双曲线
9. 【2014全国1高考理第10题】已知抛物线C:的焦点为F,准线为,P是上一点,Q是直线PF与C得一个焦点,若,则( )
A. B. C. D.
【答案】B
【解析】如图所示,因为,故,过点作,垂足为M,则轴,所以,所以,由抛物线定义知,,选B.
【考点定位】抛物线
10. 【2014全国2高考理第10题】设F为抛物线C:的焦点,过F且倾斜角为30°的直线交C于A,B两点,O为坐标原点,则
△OAB的面积为( )
A. B. C. D.
【答案】D
【解析】由题意可知:直线AB的方程为,代入抛物线的方程可得:,设A、B,则所求三角形的面积为=,故选D.
【考点定位】抛物线
11. 【2014高考安徽卷理第14题】设分别是椭圆的左、右焦点,过点的直线交椭圆于两点,若轴,则椭圆的方程为__________
【答案】
【解析】
如下图,∵轴,∴,设,又∵,则点坐标为带入椭圆为解得,所以椭圆的方程为.
【考点定位】椭圆
12. 【2014高考北京卷理第11题】设双曲线经过点(2,2),且与具有相同渐近线,则的方程为 ;渐近线方程为 .
【答案】;
【解析】因为双曲线的渐近线方程为,所以曲线的渐近线方程为,
设曲线的方程为,将代入求得,故曲线的方程为.
【考点定位】双曲线
13. 【2014江西高考理第9题】在平面直角坐标系中,分别是轴和轴上的动点,若以为直径的圆与直线相切,则圆面积的最小值为( )
A. B. C. D.
【答案】A
【解析】 设直线:.因为,所以圆心C的轨迹为以O为焦点,为准线的抛物线.圆C半径最小值为,圆面积的最小值为选A.
【考点定位】抛物线
14. 【2014山东高考理第10题】 已知,椭圆的方程为,双曲线的方程为,与的离心率之积为,则的渐近线方程为( )
A. B. C. D.
【答案】
【解析】由已知及椭圆、双曲线的几何性质得,,所以,
,双曲线的渐近线方程为,即,选.
【考点定位】椭圆、双曲线
15. 【2014四川高考理第10题】已知是抛物线的焦点,点,在该抛物线上且位于轴的两侧,(其中为坐标原点),则与面积之和的最小值是( )
A. B. C. D.
【答案】B
【解析】据题意得,设,则,或,因为位于轴两侧所以.所以两面积之和为.
【考点定位】抛物线
16. 【2014浙江高考理第16题】设直线与双曲线()两条渐近线分别交于点,若点满足,则该双曲线的离心率是__________
【答案】
【解析】有双曲线的方程可知,它的渐近线方程为,与,分别于,联立方程组,解得, ,由得,设的中点为,则,与已知直线垂直,故,解得
,即,.
【考点定位】双曲线
17. 【2014重庆高考理第8题】设分别为双曲线的左、右焦点,双曲线上存在一点使得则该双曲线的离心率为( )
B. C. D.3
【答案】B
【解析】因为是双曲线上一点,
所以,又
所以,,所以
又因为,所以有,,即
解得:(舍去),或;
所以,所以
故选B.
【考点定位】双曲线
18. 【2014天津高考理第5题】已知双曲线的一条渐近线平行于直线:,双曲线的一个焦点在直线上,则双曲线的方程为 ( )
(A) (B) (C) (D)
【答案】A
【解析】由已知得在方程中令,得
所求双曲线的方程为,故选A.
【考点定位】双曲线
19. 【2014大纲高考理第6题】已知椭圆C:的左、右焦点为、,离心率为,过的直线交C于A、B两点,若的周长为,则C的方程为 ( )
A. B. C. D.
【答案】A.
【解析】如图,的周长为
所求的椭圆成为,故选A.学科——网
【考点定位】椭圆
20. 【2014大纲高考理第9题】已知双曲线C的离心率为2,焦点为、,点A在C上,若,则( )
A. B. C. D.
【答案】A.
【解析】由已知设则由定义得
在中,由余弦定理得
,故选A.