2020届二轮复习几类不同增长的函数模型课时作业（全国通用）

2020届二轮复习几类不同增长的函数模型课时作业（全国通用）

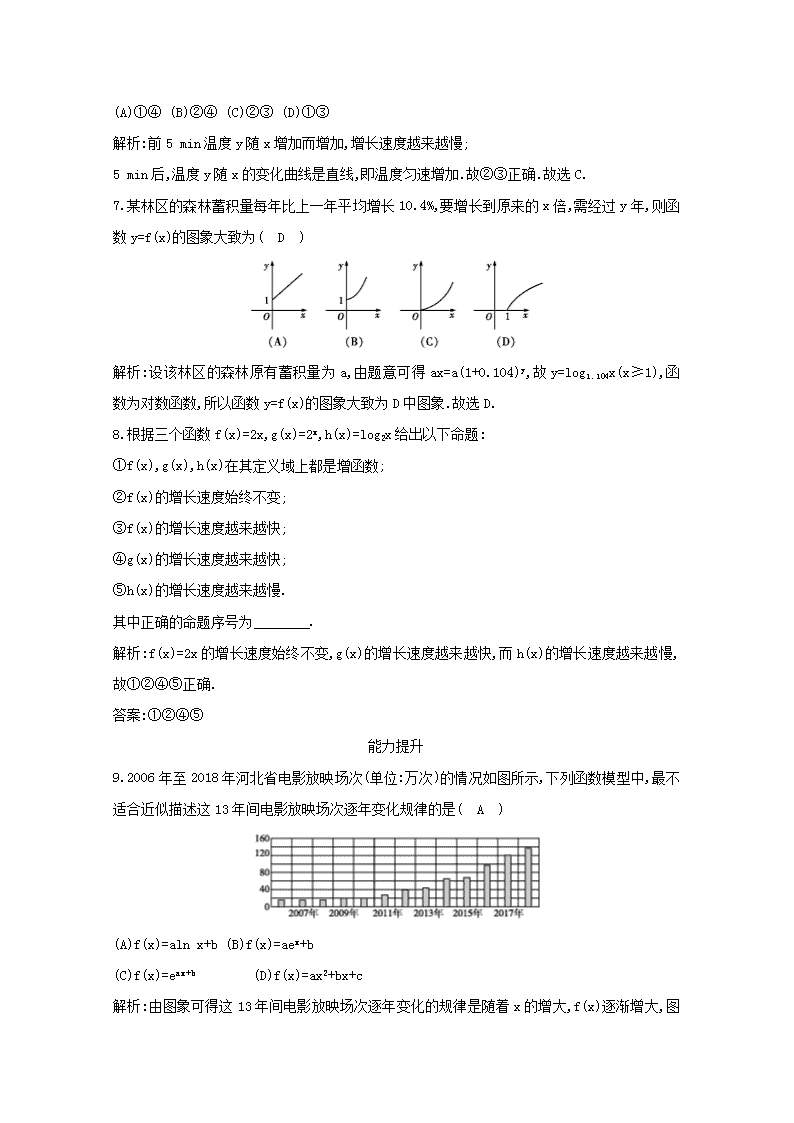
2020 届二轮复习 几类不同增长的函数模型 课时作业（全国通用） 1.已知函数 f(x)=4x,g(x)=2x,则 x∈R 时,有(　A　) (A)f(x)>g(x) (B)g(x)>f(x) (C)f(x)≥g(x) (D)g(x)≥f(x) 解析:在同一直角坐标系内,作出 f(x)=4x 与 g(x)=2x 的图象如图,可知函数 f(x)=4x 的图象在 g(x)=2x 的图象上方,故 x∈R 时,f(x)>g(x).故选 A 2.下面对函数 f(x)=lo x,g(x)=()x 与 h(x)= 在区间(0,+∞)上的递减情况说法正确的是 (　C　) (A)f(x)递减速度越来越慢,g(x)递减速度越来越快,h(x)递减速度越来越慢 (B)f(x)递减速度越来越快,g(x)递减速度越来越慢,h(x)递减速度越来越快 (C)f(x)递减速度越来越慢,g(x)递减速度越来越慢,h(x)递减速度越来越慢 (D)f(x)递减速度越来越快,g(x)递减速度越来越快,h(x)递减速度越来越快 解析:观察函数 f(x)=lo x,g(x)=()x 与 h(x)= 在区间(0,+∞)上的图象(如图)可知, 函数 f(x)的图象在区间(0,1)上递减较快,但递减速度逐渐变慢;在区间(1,+∞)上,递减较慢, 且越来越慢;同样,函数 g(x)的图象在区间(0,+∞)上,递减较慢,且递减速度越来越慢;函数 h(x)的图象在区间(0,1)上递减较快,但递减速度逐渐变慢;在区间(1,+∞)上,递减较慢,且越 来越慢.故选 C. 3.在某实验中,测得变量 x 和变量 y 之间对应数据,如表. x 0.50 1.01 2.01 3.98 y -1.01 0.01 0.98 2.00 则 x,y 最合适的函数是(　D　) (A)y=2x (B)y=x2-1 (C)y=2x-2 (D)y=log2x 解析:根据 x=0.50,y=-1.01,代入计算,可以排除 A;根据 x=2.01, y=0.98,代入计算,可以排除 B,C;将各数据代入函数 y=log2x,可知满足题意.故选 D. 4.某工厂生产 A,B 两种成本不同的产品,由于市场发生变化,A 产品连续两次提价 20%,B 产品 连续两次降价 20%,结果都以 23.04 元出售.若此时厂家同时出售 A,B 产品各一件,则相对于没 有调价时的盈亏情况是(　D　) (A)不亏不赚 (B)赚 5.92 元 (C)赚 28.96 元 (D)亏 5.92 元 解 析 : 设 A,B 两 产 品 的 原 价 分 别 为 a 元 ,b 元 , 则 a= =16,b= =36,16+36-23.04×2=5.92(元),所以比原价亏 5.92 元,故选 D. 5.在固定电压差(电压为常数)的前提下,当电流通过圆柱形的电线时,其电流强度 I 与电线半 径 r 的三次方成正比,若已知电流通过半径为 4 毫米的电线时,电流强度为 320 安,则电流通 过半径为 3 毫米的电线时,电流强度为(　D　) (A)60 安 (B)240 安 (C)75 安 (D)135 安 解析:由已知,设比例常数为 k,则 I=k·r3. 由题意,当 r=4 时,I=320,故有 320=k×43, 解得 k= =5,所以 I=5r3. 故当 r=3 时,I=5×33=135(安),故选 D. 6.在某种金属材料的耐高温实验中,温度 y(℃)随着时间 t(min)变化的情况由计算机记录后 显示的图象如图所示, 现给出下列说法: ①前 5 min 温度增加越来越快; ②前 5 min 温度增加越来越慢; ③5 min 后温度保持匀速增加; ④5 min 后温度保持不变. 其中说法正确的是(　C　) (A)①④ (B)②④ (C)②③ (D)①③ 解析:前 5 min 温度 y 随 x 增加而增加,增长速度越来越慢; 5 min 后,温度 y 随 x 的变化曲线是直线,即温度匀速增加.故②③正确.故选 C. 7.某林区的森林蓄积量每年比上一年平均增长 10.4%,要增长到原来的 x 倍,需经过 y 年,则函 数 y=f(x)的图象大致为(　D　) 解析:设该林区的森林原有蓄积量为 a,由题意可得 ax=a(1+0.104)y,故 y=log1.104x(x≥1),函 数为对数函数,所以函数 y=f(x)的图象大致为 D 中图象.故选 D. 8.根据三个函数 f(x)=2x,g(x)=2x,h(x)=log2x 给出以下命题: ①f(x),g(x),h(x)在其定义域上都是增函数; ②f(x)的增长速度始终不变; ③f(x)的增长速度越来越快; ④g(x)的增长速度越来越快; ⑤h(x)的增长速度越来越慢. 其中正确的命题序号为　　　　. 解析:f(x)=2x 的增长速度始终不变,g(x)的增长速度越来越快,而 h(x)的增长速度越来越慢, 故①②④⑤正确. 答案:①②④⑤ 能力提升 9.2006 年至 2018 年河北省电影放映场次(单位:万次)的情况如图所示,下列函数模型中,最不 适合近似描述这 13 年间电影放映场次逐年变化规律的是(　A　) (A)f(x)=aln x+b (B)f(x)=aex+b (C)f(x)=eax+b (D)f(x)=ax2+bx+c 解析:由图象可得这 13 年间电影放映场次逐年变化的规律是随着 x 的增大,f(x)逐渐增大,图 象逐渐上升.对于 A,a>0 时,为“上凸函数”,不符合图象的特征;a<0 时,为单调递减函数,不符 合图象的特征;对于 B,取 a>0,b>0,可得满足条件的函数;对于 C,取 a>0,b>0,可得满足条件的 函数;对于 D,f(x)=ax2+bx+c,取 a>0,- <0,可得满足条件的函数.故选 A. 10.某地发生地震后,地震专家对该地区发生的余震进行了监测,记录的部分数据如下表: 强度(J) 1.6×1019 3.2×1019 4.5×1019 6.4×1019 震级(里氏) 5.0 5.2 5.3 5.4 注:地震强度是指地震时释放的能量.地震强度(x)和震级(y)的模拟函数关系可以选用 y=alg x+b(其中 a,b 为常数).利用图可知 a 的值等于　　　　. (取 lg 2=0.3 进行计算) 解析:由模拟函数及题图得 两式相减得 a(lg 3.2-lg 1.6)=0.2,alg 2=0.2, a=. 答案: 探究创新 11.(2018·江西宜春高一检测)某人对东北一种松树的生长进行了研究,收集了其高度 h(米) 与生长时间 t(年)的相关数据,选择 h=mt+b 与 h=loga(t+1)来刻画 h 与 t 的关系,你认为哪个 符合?并预测第 8 年的松树高度. t(年) 1 2 3 4 5 6 h(米) 0.6 1 1.3 1.5 1.6 1.7 解:据表中数据作图如图. 由图可以看出用一次函数模型不吻合,选用对数型函数比较合理. 不妨将(2,1)代入到 h=loga(t+1)中,得 1=loga3,解得 a=3. 故可用函数 h=log3(t+1)来拟合这个实际问题. 当 t=8 时,h=log3(8+1)=2. 故可预测第 8 年松树的高度为 2 米. [教师备用 1] 三个变量 y1,y2,y3 随着变量 x 的变化情况如下表: x 1 3 5 7 9 11 y1 5 135 625 1 715 3 635 6 655 y2 5 29 245 2 189 19 685 177 149 y3 5 6.10 6.61 6.95 7.20 7.40 则与 x 呈对数型函数、指数型函数、幂函数型函数变化的变量依次是(　C　) (A)y1,y2,y3 (B)y2,y1,y3 (C)y3,y2,y1 (D)y3,y1,y2 解析:三种常见的增长型函数中,由于指数型函数呈爆炸性增长,对数型函数增长越来越慢,幂 函数的增长介于两者之间,结合表中数据可知,y2 是指数型函数,y3 是对数型函数.故选 C. [教师备用 2] (2019·福建省宁德市部分一级达标学校高一上期中)水葫芦原产于巴西,1901 年作为观赏植物引入中国.现在南方一些水域水葫芦已泛滥成灾严重影响航道安全和水生动 物生长.某科研团队在某水域放入一定量水葫芦进行研究,发现其蔓延速度越来越快,经过 2 个月其覆盖面积为 18 m2,经过 3 个月其覆盖面积为 27 m2.现水葫芦覆盖面积 y(单位 m2)与经过 时间 x(x∈N)个月的关系有两个函数模型 y=kax(k>0,a>1)与 y=p +q(p>0)可供选择.(参考数 据: ≈1.414, ≈1.732,lg 2≈0.301 0,lg 3≈0.477 1) (1)试判断哪个函数模型更合适,并求出该模型的解析式; (2)求原先投放的水葫芦的面积并求约经过几个月该水域中水葫芦面积是当初投放的 1 000 倍. 解:(1)因为 y=kax(k>0,a>1)的增长速度越来越快,y=p +q(p>0)的增长速度越来越慢, 所以依题意应选函数 y=kax(k>0,a>1),则有 解得 所以 y=8×()x(x∈N). (2)当 x=0 时,y=8. 设经过 x 个月该水域中水葫芦面积是当初投放的 1 000 倍. 由题意得 8·()x=8×1 000, 所以 x=lo 1 000= = ≈17. 答:原先投放的水葫芦的面积为 8 m2,约经过 17 个月该水域中水葫芦面积是当初投放的 1 000 倍.