2019届二轮复习(文)1-2-2数形结合思想课件（15张）

2019届二轮复习(文)1-2-2数形结合思想课件（15张）

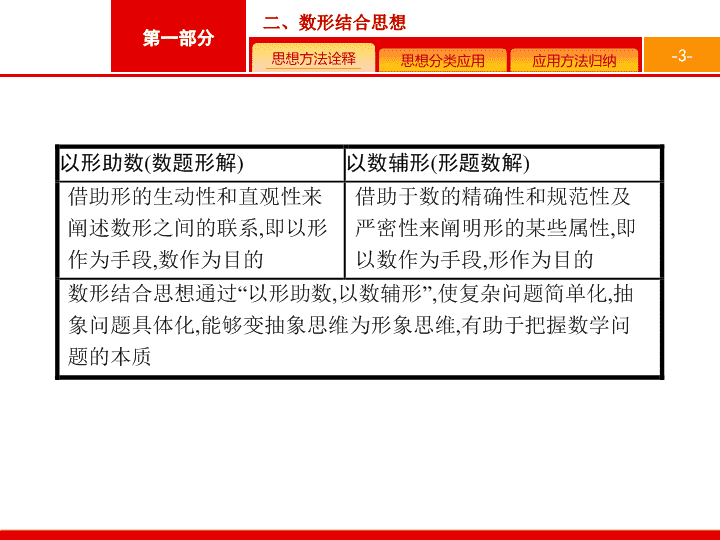
二、数形结合思想 - 2 - 数形结合思想是解答高考数学试题的一种常用方法与技巧 , 在高考试题中 , 数形结合思想主要用于解选择题和填空题 , 有直观、简单、快捷等特点 ; 而在解答题中 , 考虑到推理论证的严密性 , 图形只是辅助手段 , 最终要用 “ 数 ” 写出完整的解答过程 . - 3 - - 4 - 应用 一 应用二 应用三 应用一 　 利用数形结合求与方程根有关的问题   例 1 (2018 山东师大附中一模 , 文 12) 函数 f ( x ) 是定义在 R 上的偶函数 , 且满足 f ( x+ 2) =f ( x ), 当 x ∈ [0,1] 时 , f ( x ) = 2 x , 若在区间 [ - 2,3] 上方程 ax+ 2 a-f ( x ) = 0 恰有四个不相等的实数根 , 则实数 a 的取值范围是 ( 　　 ) 答案 : D - 5 - 应用 一 应用二 应用三 解析 : 若在区间 [ - 2,3] 上方程 ax+ 2 a-f ( x ) = 0 恰有四个不相等的实数根 , 等价于 f ( x ) =a ( x+ 2) 有四个不相等的实数根 , 即函数 y=f ( x ) 和 g ( x ) =a ( x+ 2) 有四个不同的交点 , ∵ f ( x+ 2) =f ( x ), ∴ 函数 f ( x ) 的周期为 2, 当 - 1 ≤ x ≤ 0 时 ,0 ≤ -x ≤ 1, 此时 f ( -x ) =- 2 x. ∵ f ( x ) 是定义在 R 上的偶函数 , ∴ f ( -x ) =- 2 x=f ( x ), 即 f ( x ) =- 2 x , - 1 ≤ x ≤ 0 . 作出函数 f ( x ) 和 g ( x ) 的图象 , - 6 - 应用 一 应用二 应用三 - 7 - 应用 一 应用二 应用三 思维升华 讨论方程的解 ( 或函数的零点 ) 的个数一般可构造两个函数 , 转化为讨论两曲线 ( 或曲线与直线等 ) 的交点个数 , 其基本步骤是先把方程两边的代数式看作是两个熟悉函数的表达式 ( 不熟悉时 , 需要作适当变形转化为两个熟悉的函数 ), 再在同一平面直角坐标系中作出两个函数的图象 , 图象的交点个数即为方程解 ( 或函数零点 ) 的个数 . - 8 - 应用 一 应用二 应用三 突破训练 1 若实数 a 满足 a+ lg a= 4, 实数 b 满足 b+ 10 b = 4, 函数 则 关于 x 的方程 f ( x ) =x 的根的个数是 ( 　　 ) A . 1 B . 2 C . 3 D . 4 答案 解析 解析 关闭 答案 解析 关闭 - 9 - 应用一 应用二 应用三 应用二 　 利用数形结合求参数范围及解不等式   例 2 (2018 河南郑州一模 , 理 14) 已知 函数 若 不等式 f ( x ) ≤ 5 -mx 恒成立 , 则实数 m 的取值范围是 　　　　　 .   答案 解析 解析 关闭 答案 解析 关闭 - 10 - 应用一 应用二 应用三 思维升华 在解含有参数的不等式时 , 由于涉及参数 , 往往需要讨论 , 导致演算过程烦琐冗长 . 如果题设与几何图形有联系 , 那么利用数形结合的方法 , 问题将会简练地得到解决 . - 11 - 应用一 应用二 应用三 答案 解析 解析 关闭 答案 解析 关闭 - 12 - 应用一 应用二 应用三 应用三 　 数形结合在解析几何中的应用   例 3 已知圆 C :( x- 3) 2 + ( y- 4) 2 = 1 和两点 A ( -m ,0), B ( m ,0)( m> 0) . 若圆 C 上存在点 P , 使得 ∠ APB= 90 ° , 则实数 m 的最大值为 ( 　　 ) A.7 B.6 C.5 D.4 答案 解析 解析 关闭 答案 解析 关闭 - 13 - 应用一 应用二 应用三 思维升华 1 . 如果等式、代数式的结构蕴含着明显的几何特征 , 那么就要考虑用数形结合的思想方法来解题 , 即所谓的几何法求解 , 比较常见的有 : 2 . 解析几何中的一些范围及最值问题 , 常结合几何图形的性质 , 使问题得到简便快捷的解决 . - 14 - 应用一 应用二 应用三 突破训练 3 如图 , 过抛物线 y 2 = 2 px ( p> 0) 的焦点 F 的直线依次交抛物线及准线于点 A , B , C , 若 |BC|= 2 |BF| , 且 |AF|= 3, 则抛物线的方程为 ( 　　 ) 答案 解析 解析 关闭 答案 解析 关闭 - 15 - 方程思想在解题中的应用主要表现在四个方面 : (1) 解方程或解不等式 ; (2) 含参数的方程或不等式的讨论 , 常涉及一元二次方程的判别式、根与系数的关系、区间根、区间上恒成立等知识的应用 ; (3) 需要转化为方程的讨论 , 如曲线的位置关系等 ; (4) 构造方程或不等式求解问题 .