2019届二轮复习直线的一般式方程课件（20张）

2019届二轮复习直线的一般式方程课件（20张）

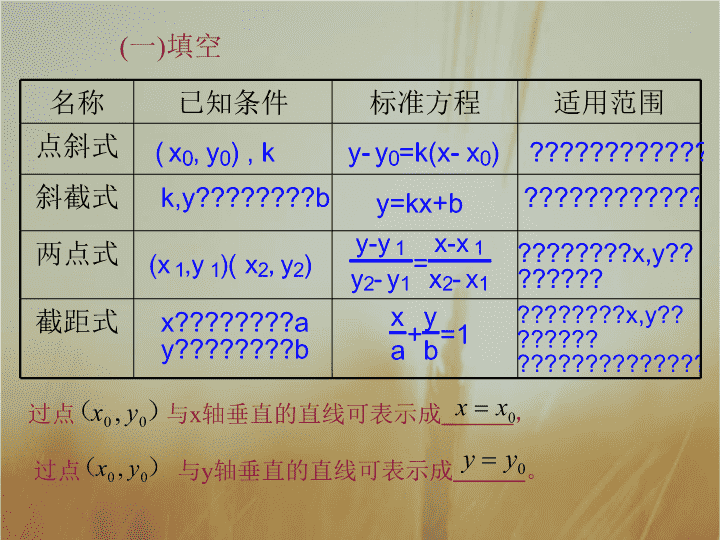
直线的一般式方程 ( 一 ) 填空 名称 已知条件 标准方程 适用范围 点斜式 斜截式 两点式 截距式 过点 与 x 轴垂直的直线可表示成 ， 过点 与 y 轴垂直的直线可表示成 。 （二）填空 1 ．过点 (2,1) ，斜率为 2 的直线的方程是 ____________ 2 ．过点 (2,1) ，斜率为 0 的直线方程是 ___________ 3 ．过点 (2,1) ，斜率不存在的直线的方程是 _________ 思考 1 ：以上三个方程是否都是二元一次方程 ? 所有的直线方程是否都是二元一次方程？ 1.明确直线方程一般式的形式特征 . （重点） 2.会把直线方程的一般式化为斜截式，进而求斜率 和截距 . （难点） 3.会把直线方程的点斜式、两点式化为一般式. （难点） Ax+By+C=0(A,B 不同时为 0 ） 我们把关于 x,y 的二元一次方程 叫做直线的一般式方程，简称一般式 . 一般式适用于任意一条直线 . 探究 1 ：直线的一般式方程 特别： 对于直线方程的一般式，一般作如下约定： x的系数为正，x,y的系数及常数项一般不出现分数，一般按含x项、y项、常数项的顺序排列. 直线的点斜式、斜截式、两点式、截距式方程都是关于 x ， y 的方程，上述四种直线方程，能否写成如 Ax+ By+C=0 （ A,B 不同时为 0 ）的统一形式？ 点斜式： 探究2：一般式方程与其他形式方程的转化 斜截式： y=kx+b kx-y+b=0 两点式： （ y 1 -y 2 ） x+(x 2 -x 1 )y+ x 1 y 2 -x 2 y 1 =0 截距式： bx+ay-ab=0 例 1 已知直线经过点 A （ 6 ， - 4 ），斜率为 ，求直线的点斜式和一般式方程 . 解： 经过点 A(6 ， -4), 斜率为 的直线的点斜式 方程为 化成一般式，得 4x+3y-12=0. 例 2 把直线 l 的一般式方程 x-2y+6=0 化成斜截式，求出直线 l 的斜率以及它在 x 轴与 y 轴上的截距，并画出图形 . 解： 将原方程化成斜截式得 因此，直线 l 的斜率 ，它在 y 轴上的截距是 3 ， 在直线 l 的方程 x-2y+6=0 中， x y O -6 3 令 y=0 ，可得 x=-6 ，即直线 l 在 x 轴上的截距是 -6. 例 3 已知直线 l 1 ： ax+(a+1)y-a=0 和 l 2 ： (a+2)x+2(a+1)y-4=0 ，若 l 1 // l 2 ，求 a 的值 . 1. 若直线 l 在 x 轴上的截距为 -4 ，倾斜角的正切值为 1 ， 则直线 l 的点斜式方程是 ___________. 直线 l 的斜截式方程是 ___________. 直线 l 的一般式方程是 ___________. y-0=x+4 y=x+4 x-y+4=0 解： (1)x+2y-4=0 . 2. 根据下列条件，写出直线的一般式方程： (2)y-2=0 . (3)2x-y-3=0 . (4)x+y-1=0. y x O 5 x y O -5 4 3. 求下列直线的斜率以及在 y 轴上的截距，并画出图形 . （ -2,1 ） x O y x O y 4.已知线段PQ两端点的坐标分别为P(-1，1)和 Q(2，2)，若直线 l :x+my+m=0与线段PQ有交点， 求实数m的取值范围. 解： 如图所示，直线 l :x+my+m=0过定点 A(0，-1)，当m≠0时， 解得 或 当 m=0 时，直线 l 的方程为 x=0 ，与线段 PQ 有交点，所以，实数 m 的取值范围为 1. 直线方程的一般式 Ax+By+C=0 （ A ， B 不同时为 0 ） 2. 直线方程的一般式与特殊式的互化 . 3. 两条直线平行与垂直的判定 .