2019届二轮复习(文)小题标准练(八)作业(全国通用)
温馨提示:
此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。关闭Word文档返回原板块。
小题标准练(八)
(40分钟 80分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知i为虚数单位,则|3+2i|= ( )
A. B. C. D.3
【解析】选C.由题意得|3+2i|==.
2.已知A={x|-2
1},则A∩(∁RB)为 ( )
A.(-2,1) B.(-∞,1)
C.(0,1) D.(-2,0]
【解析】选D.由题意得集合B={x|x>0},所以∁RB={x|x≤0},则A∩(∁RB)={x|-2b>c,且a+b+c=0,求证0 B.a-c>0
C.(a-b)(a-c)>0 D.(a-b)(a-c)<0
【解析】选C.0⇔(a-c)(2a+c)>0⇔(a-c)(a-b)>0.
5.函数y=e-|x-1|的图象大致形状是 ( )
【解析】选B.记f(x)=e-|x-1|,显然f(1)=1,
f(0)=<1.
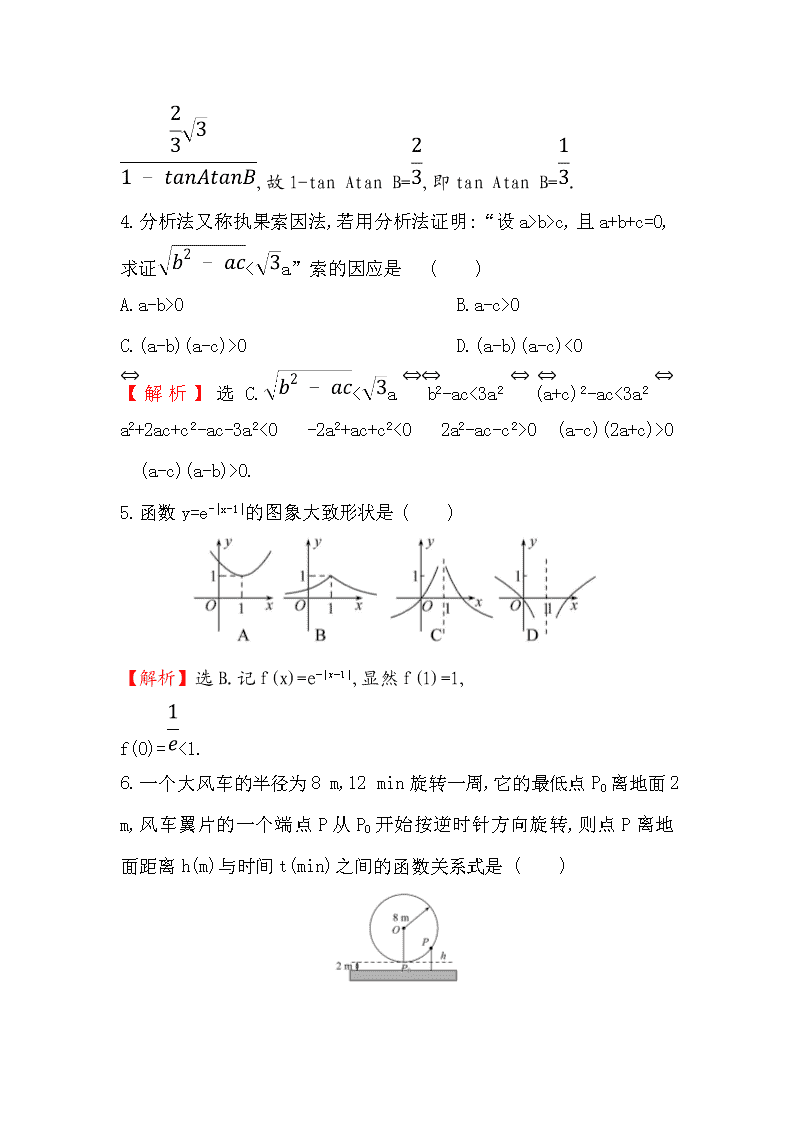
6.一个大风车的半径为8 m,12 min旋转一周,它的最低点P0离地面2 m,风车翼片的一个端点P从P0开始按逆时针方向旋转,则点P离地面距离h(m)与时间t(min)之间的函数关系式是 ( )
A.h(t)=-8sint+10 B.h(t)=-8cost+10
C.h(t)=-8sint+8 D.h(t)=-8cost+8
【解析】选B.过P作OP0的垂线,垂足为D,连接DP.h=10-OD,而OD=8cos t
=8cos t,所以h=10-8cos t.
7.函数f(x)=tan2x-的单调递增区间是 ( )
A.(k∈Z)
B.(k∈Z)
C.(k∈Z)
D.(k∈Z)
【解析】选B.当kπ-<2x-
2f′(x),若20.所以x>2时,f′(x)>0,x<2时,f′(x)<0,即 f(x)在(-∞,2)上递减,在(2,+∞)上递增,因为22,0<<≤,0<2-<2,如图,
所以f0)的焦点为F,准线为l.过抛物线上一点A作l的垂线,垂足为B.设C,AF与BC相交于点E.若|CF|=2|AF|,且△ACE的面积为3,则p的值为 ( )
A. B. C.2 D.
【解析】选D.抛物线的普通方程为y2=2px,F,
|CF|=p-=3p,又|CF|=2|AF|,则|AF|=p,
由抛物线的定义得|AB|=p,所以xA=p,则|yA|=p,由CF∥AB得=,即==2,所以SΔCEF=2SΔCEA=6,SΔACF=SΔAEC+SΔCFE=9,
所以×3p×p=9,p=.
12.记min{x,y}=设f(x)=min{x2,x3},则 ( )
A.存在t>0,|f(t)+f(-t)|>f(t)-f(-t)
B.存在t>0,|f(t)-f(-t)|>f(t)-f(-t)
C.存在t>0,|f(1+t)+f(1-t)|>f(1+t)+f(1-t)
D.存在t>0,|f(1+t)-f(1-t)|>f(1+t)-f(1-t)
【解析】选C.由x2-x3=x2(1-x)≤0得x≥1,所以f(x)=min{x2,x3}=当t>1时,|f(t)+f(-t)|=|t2+(-t)3|=t3-t2,|f(t)-f(-t)|=|t2-(-t)3|=t3+t2,f(t)-
f(-t)=t2-(-t)3=t3+t2,所以|f(t)+f(-t)|0时,设g(t)=f(1+t)+f(1-t)=(1+t)2+(1-t)3=-t3+4t2-t+2,则g′(t)=-3t2+8t-1,令-3t2+8t-1=0得t=,所以函数g(t)在上单调递减,所以存在t0∈使得g(t0)<0成立,所以存在t0∈,使得|f(1+t0)+f(1-t0)|≥0>f(1+t0)+f(1-t0),
C正确;当t>0时,设h(t)=f(1+t)-f(1-t)=(1+t)2-(1-t)3=t3-2t2+5t,则
h′(t)=3t2-4t+5=3+>0,所以函数h(t)在(0,+∞)上单调递增,所以h(t)>h(0)=0,所以|f(1+t)-f(1-t)|=f(1+t)-f(1-t),D错误.
二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)
13.在△ABC中,a,b,c分别是角A,B,C的对边,且=-,则角B的值为____________.
【解析】方法一:由正弦定理,即===2R,得a=2Rsin
A,b=2Rsin B, c=2Rsin C,代入=-,得=-,
即2sin Acos B+sin Ccos B+cos Csin B=0,
所以2sin Acos B+sin(B+C)=0.
在△ABC中,sin(B+C)=sin A,所以2sin Acos B+sin A=0,又sin A≠0,所以
cos B=-.又角B为△ABC的内角,所以B=.
方法二:由余弦定理,即cos B=,
cos C=,代入=-,
得·=-,整理,得a2+c2-b2=-ac,
所以cos B==-=-,又角B为△ABC的内角,所以B=.
答案:
14.如图,已知球O的面上有四点A,B,C,D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=,则球O的体积等于____________.
【解析】如图,以DA,AB,BC为棱长构造正方体,
设正方体的外接球球O的半径为R,则正方体的体对角线长即为球O的直径,
所以CD==2R,所以R=,
故球O的体积V==π.
答案:π
15.图1是某学生的数学成绩茎叶图,第1次到14次的考试成绩依次记为A1,A2,…,A14.图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图,那么算法流程图输出的结果是____________.
【解析】由程序框图知:算法的功能是计算学生在14次数学考试成绩中,成绩大于等于90的次数,由茎叶图得,在14次测试中,成绩大于等于90的有:93, 99,98,98,94,91,95,103,101,114共10次,所以输出n的值为10.
答案:10
16.若直线y=kx+b是曲线y=ln x+2的切线,也是曲线y=ln(x+1)的切线,则b=_______________.
【解析】对函数y=ln x+2求导数得y′=,对函数y=ln(x+1)求导数得y′=,设直线y=kx+b与函数y=ln x+2相切于点P1,与函数y=ln(x+1)相切于点P2,则y1=ln x1+2,y2=ln,所以切线方程分别为y-=,y-ln=,这两条切线都是y=kx+b,所以k==,b=1+ln x1=ln-,解得x1=,b=1+ln=1-
ln 2.
答案:1-ln 2
关闭Word文档返回原板块