2019届二轮复习选择填空标准练(7)作业(全国通用)
2019届二轮复习 选择填空标准练 (7) 作业(全国通用)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合A={x|-1
a>1”是“logax>0”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既非充分也非必要条件
【解析】选A.若logax>0=loga1,当0a>1时,则logax>loga1=0,充分性成立,
故“x>a>1”是“logax>0”的充分而不必要条件.
7.口袋中装有大小、轻重都无差别的5个红球和4个白球,每一次从袋中摸出2个球,若颜色不同,则为中奖,每次摸球后,都将摸出的球放回口袋中,则3次摸球恰有1次中奖的概率为 ( )
A. B. C. D.
【解析】选A.每次摸球中奖的概率为==,由于是有放回地摸球,
故3次摸球相当于3次独立重复试验,
所以3次摸球恰有1次中奖的概率
P=××1-2=.
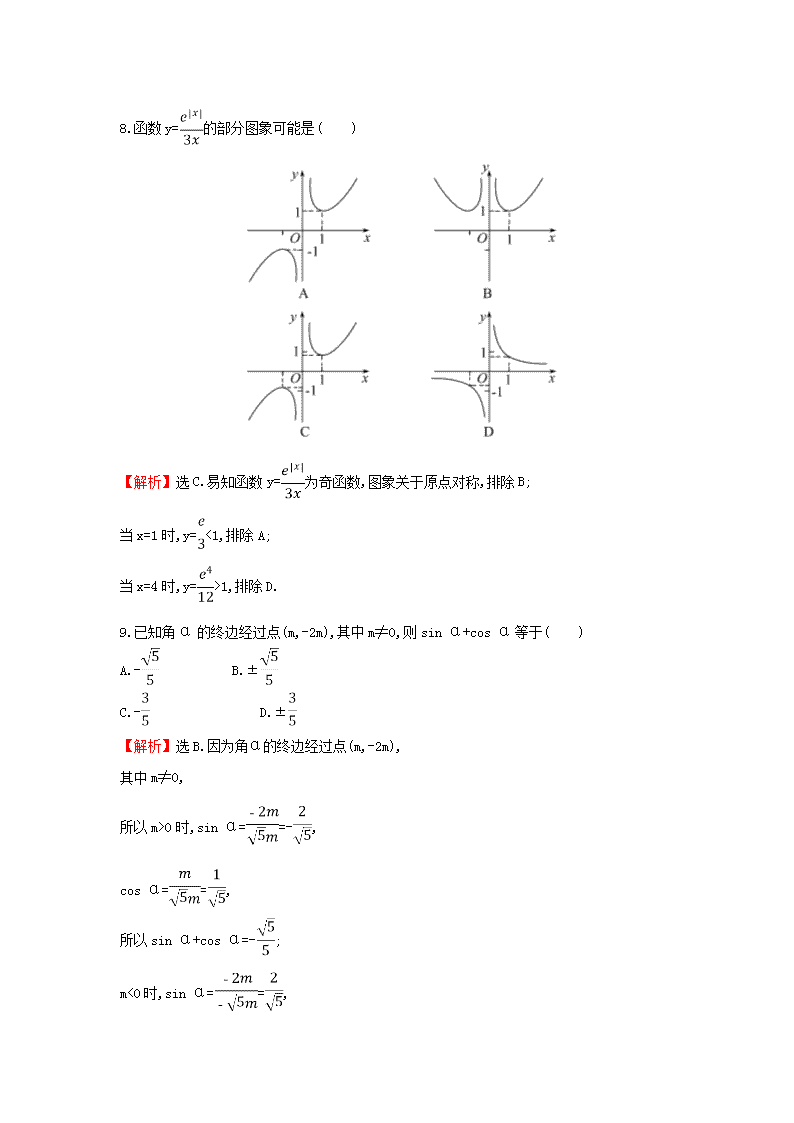
8.函数y=的部分图象可能是 ( )
【解析】选C.易知函数y=为奇函数,图象关于原点对称,排除B;
当x=1时,y=<1,排除A;
当x=4时,y=>1,排除D.
9.已知角α的终边经过点(m,-2m),其中m≠0,则sin α+cos α等于( )
A.- B.±
C.- D.±
【解析】选B.因为角α的终边经过点(m,-2m),
其中m≠0,
所以m>0时,sin α==-,
cos α==,
所以sin α+cos α=-;
m<0时,sin α==,
cos α==-,
所以sin α+cos α=;
所以sin α+cos α=± .
10.执行如图所示的程序框图,则输出的S= ( )
A. B. C. D.
【解析】选B.运行程序如下:S=,n=4,4<19.
S=+,n=6,6<19.
S=++,n=8,8<19.
……
S=+++…+,n=20,20>19.
S=+++…+=-+-+…+-=.
11.若函数f(x)=sin(π-ωx)+sin+ωx(ω>0),且f(α)=2,
f(β)=0,|α-β|的最小值是,则f(x)的单调递增区间是 ( )
A.(k∈Z)
B.(k∈Z)
C.(k∈Z)
D.(k∈Z)
【解析】选A.由题意可得f(x)=sin(π-ωx)+sin+ωx=sin ωx+
cos ωx=2sinωx+,由f(α)=2,f(β)=0,|α-β|的最小值是,所以=·=,所以ω=1,f(x)=2sinx+.
令2kπ-≤x+≤2kπ+,k∈Z,求得2kπ-≤x≤2kπ+,
故函数的增区间为(k∈Z).
12.已知函数f(x)=若数列{an}满足an=f(n)(n∈N*),且{an}是递减数列,则实数a的取值范围是 ( )
A. B.
C. D.
【解析】选C.由已知可得1-2a<0,0a13=1,解得0)的焦点,过F作倾斜角为30°的直线l与抛物线E交于A,B两点,过A,B向E的准线作垂线,垂足分别为C,D,设CD的中点为M,则|MF|=________.
【解析】直线的方程为y-0=x-
=x-p,
联立直线和抛物线的方程得4x2-28px+p2=0,
设A(x1,y1),B(x2,y2),
则x1+x2=7p,
所以AB的中点N的横坐标为=p,
所以N的纵坐标为y=×p-p=p.
所以|MF|==2p.
答案:2p
15.在△ABC中,sin B=3sin A,BC=,且C=,则AB边上的高为________.
【解析】根据正弦定理可得b=3a,由BC=可得AC=6,由余弦定理:
cos =⇒c=,设AB边上的高为h,由等面积法可得:absin C=ch⇒h=,故AB边上的高为.
答案:
16.已知函数f(x)=sin(ωx+φ),若f=f=0,则f(π)=________.
【解析】因为周期T=,
0<ω<3,所以T=>.
因为-=,
因为f=f=0,
所以,为相邻的平衡点.
所以T==×2=π,
所以ω=2.所以f(x)=sin(2x+φ) .
因为f=0,
所以sin=sin=0,
所以-+φ=kπ,
所以φ=+kπ(k∈Z).
因为|φ|<,所以φ=.
所以f(x)=sin,
所以f(π)=sin=sin=.
答案: