2018届二轮复习空间中位置关系的判断与证明问题课件文（全国通用）

2018届二轮复习空间中位置关系的判断与证明问题课件文（全国通用）

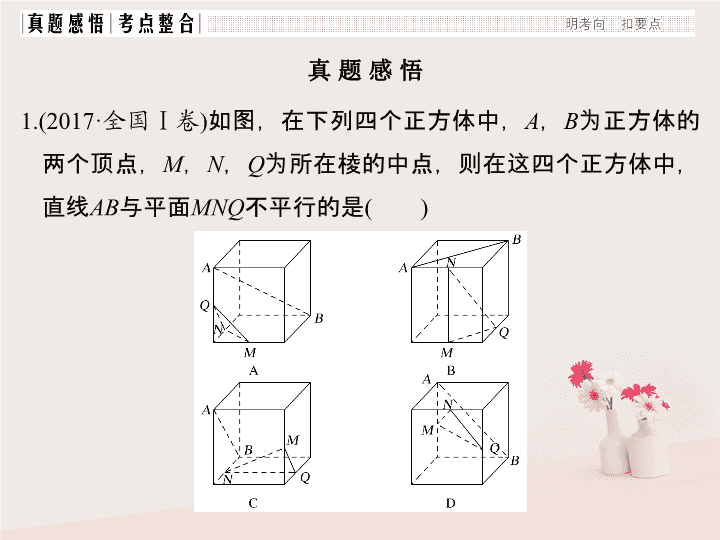
第 2 讲　空间中位置关系的判断与证明问题 高考定位　 1. 以几何体为载体考查空间点、线、面位置关系的判断，主要以选择、填空题的形式，题目难度较小； 2. 以解答题的形式考查空间平行、垂直的证明，并常与几何体的表面积、体积相渗透 . 真 题 感 悟 1. (2017· 全国 Ⅰ 卷 ) 如图，在下列四个正方体中， A ， B 为正方体的两个顶点， M ， N ， Q 为所在棱的中点，则在这四个正方体中，直线 AB 与平面 MNQ 不平行的是 ( 　　 ) 解析　法一 　 对于选项 B ，如图 (1) 所示，连接 CD ，因为 AB ∥ CD ， M ， Q 分别是所在棱的中点，所以 MQ ∥ CD ，所以 AB ∥ MQ ，又 AB ⊄ 平面 MNQ ， MQ ⊂ 平面 MNQ ，所以 AB ∥ 平面 MNQ . 同理可证选项 C ， D 中均有 AB ∥ 平面 MNQ . 因此 A 项不正确 . 图 (1) 　　　　　　图 (2) 法二 　 对于选项 A ，其中 O 为 BC 的中点 ( 如图 (2) 所示 ) ，连接 OQ ，则 OQ ∥ AB ，因为 OQ 与平面 MNQ 有交点，所以 AB 与平面 MNQ 有交点，即 AB 与平面 MNQ 不平行 .A 项不正确 . 答案　 A 2. (2016· 全国 Ⅱ 卷 ) α ， β 是两个平面， m ， n 是两条直线，有下列四个命题： ① 如果 m ⊥ n ， m ⊥ α ， n ∥ β ，那么 α ⊥ β . ② 如果 m ⊥ α ， n ∥ α ，那么 m ⊥ n . ③ 如果 α ∥ β ， m ⊂ α ，那么 m ∥ β . ④ 如果 m ∥ n ， α ∥ β ，那么 m 与 α 所成的角和 n 与 β 所成的角相等 . 其中正确的命题有 ________( 填写所有正确命题的编号 ). 解析　 当 m ⊥ n ， m ⊥ α ， n ∥ β 时，两个平面的位置关系不确定，故 ① 错误，经判断知 ②③④ 均正确，故正确答案为 ②③④ . 答案　 ②③④ 解析　 如图所示，设平面 CB 1 D 1 ∩ 平面 ABCD ＝ m 1 ，因为 α ∥ 平面 CB 1 D 1 ，所以 m 1 ∥ m ， 答案　 A 4. (2017· 全国 Ⅰ 卷 ) 如图，在四棱锥 P － ABCD 中， AB ∥ CD ，且 ∠ BAP ＝ ∠ CDP ＝ 90°. (1) 证明　 ∵∠ BAP ＝ ∠ CDP ＝ 90° ， ∴ AB ⊥ PA ， CD ⊥ PD . ∵ AB ∥ CD ， ∴ AB ⊥ PD . 又 ∵ PA ∩ PD ＝ P ， PA ， PD ⊂ 平面 PAD ， ∴ AB ⊥ 平面 PAD . ∵ AB ⊂ 平面 PAB ， ∴ 平面 PAB ⊥ 平面 PAD . (2) 解　 取 AD 的中点 E ， 连接 PE . ∵ PA ＝ PD ， ∴ PE ⊥ AD . 由 (1) 知， AB ⊥ 平面 PAD ， 故 AB ⊥ PE ， AB ⊥ AD ，可得 PE ⊥ 平面 ABCD . 考 点 整 合 1. 直线、平面平行的判定及其性质 (1) 线面平行的判定定理： a ⊄ α ， b ⊂ α ， a ∥ b ⇒ a ∥ α . (2) 线面平行的性质定理： a ∥ α ， a ⊂ β ， α ∩ β ＝ b ⇒ a ∥ b . (3) 面面平行的判定定理： a ⊂ β ， b ⊂ β ， a ∩ b ＝ P ， a ∥ α ， b ∥ α ⇒ α ∥ β . (4) 面面平行的性质定理： α ∥ β ， α ∩ γ ＝ a ， β ∩ γ ＝ b ⇒ a ∥ b . (1) 线面垂直的判定定理： m ⊂ α ， n ⊂ α ， m ∩ n ＝ P ， l ⊥ m ， l ⊥ n ⇒ l ⊥ α . (2) 线面垂直的性质定理： a ⊥ α ， b ⊥ α ⇒ a ∥ b . (3) 面面垂直的判定定理： a ⊂ β ， a ⊥ α ⇒ α ⊥ β . (4) 面面垂直的性质定理： α ⊥ β ， α ∩ β ＝ l ， a ⊂ α ， a ⊥ l ⇒ a ⊥ β . 2. 直线、平面垂直的判定及其性质 热点一　空间点、线、面位置关系的判定 【例 1 】 　 (2017· 成都诊断 ) 已知 m ， n 是空间中两条不同的直线， α ， β 是两个不同的平面，且 m ⊂ α ， n ⊂ β . 有下列命题： ① 若 α ∥ β ，则 m ∥ n ； ② 若 α ∥ β ，则 m ∥ β ； ③ 若 α ∩ β ＝ l ，且 m ⊥ l ， n ⊥ l ，则 α ⊥ β ； ④ 若 α ∩ β ＝ l ，且 m ⊥ l ， m ⊥ n ，则 α ⊥ β . 其中真命题的个数是 ( 　　 ) A.0 B.1 C.2 D.3 解析　 ① 若 α ∥ β ，则 m ∥ n 或 m ， n 异面，不正确； ② 若 α ∥ β ，根据平面与平面平行的性质，可得 m ∥ β ，正确； ③ 若 α ∩ β ＝ l ，且 m ⊥ l ， n ⊥ l ，则 α 与 β 不一定垂直，不正确； ④ 若 α ∩ β ＝ l ，且 m ⊥ l ， m ⊥ n ， l 与 n 不一定相交，不能推出 α ⊥ β ，不正确 . 答案　 B 探究提高　 判断与空间位置关系有关的命题真假的方法 (1) 借助空间线面平行、面面平行、线面垂直、面面垂直的判定定理和性质定理进行判断 . (2) 借助空间几何模型，如从长方体模型、四面体模型等模型中观察线面位置关系，结合有关定理，进行肯定或否定 . (3) 借助于反证法，当从正面入手较难时，可利用反证法，推出与题设或公认的结论相矛盾的命题，进而作出判断 . 【训练 1 】 (2017· 广东省际名校联考 ) 已知 α ， β 为平面， a ， b ， c 为直线，下列命题正确的是 ( 　　 ) A. a ⊂ α ，若 b ∥ a ，则 b ∥ α B. α ⊥ β ， α ∩ β ＝ c ， b ⊥ c ，则 b ⊥ β C. a ⊥ b ， b ⊥ c ，则 a ∥ c D. a ∩ b ＝ A ， a ⊂ α ， b ⊂ α ， a ∥ β ， b ∥ β ，则 α ∥ β 解析　 选项 A 中， b ⊂ α 或 b ∥ α ，不正确 . B 中 b 与 β 可能斜交， B 错误 . C 中 a ∥ c ， a 与 c 异面，或 a 与 c 相交， C 错误 . 利用面面平行的判定定理，易知 D 正确 . 答案　 D 热点二　空间平行、垂直关系的证明 【例 2 】 　如图，在四棱锥 P － ABCD 中， AB ∥ CD ， AB ⊥ AD ， CD ＝ 2 AB ，平面 PAD ⊥ 底面 ABCD ， PA ⊥ AD ， E 和 F 分别是 CD 和 PC 的中点，求证： (1) PA ⊥ 底面 ABCD ； (2) BE ∥ 平面 PAD ； (3) 平面 BEF ⊥ 平面 PCD . 证明　 (1) ∵ 平面 PAD ⊥ 底面 ABCD ， 且 PA 垂直于这两个平面的交线 AD ， PA ⊂ 平面 PAD ， ∴ PA ⊥ 底面 ABCD . (2) ∵ AB ∥ CD ， CD ＝ 2 AB ， E 为 CD 的中点， ∴ AB ∥ DE ，且 AB ＝ DE . ∴ 四边形 ABED 为平行四边形 . ∴ BE ∥ AD . 又 ∵ BE ⊄ 平面 PAD ， AD ⊂ 平面 PAD ， ∴ BE ∥ 平面 PAD . (3) ∵ AB ⊥ AD ，而且 ABED 为平行四边形 . ∴ BE ⊥ CD ， AD ⊥ CD ， 由 (1) 知 PA ⊥ 底面 ABCD . ∴ PA ⊥ CD ，且 PA ∩ AD ＝ A ， PA ， AD ⊂ 平面 PAD ， ∴ CD ⊥ 平面 PAD ，又 PD ⊂ 平面 PAD ， ∴ CD ⊥ PD . ∵ E 和 F 分别是 CD 和 PC 的中点， ∴ PD ∥ EF . ∴ CD ⊥ EF ，又 BE ⊥ CD 且 EF ∩ BE ＝ E ， ∴ CD ⊥ 平面 BEF ，又 CD ⊂ 平面 PCD ， ∴ 平面 BEF ⊥ 平面 PCD . 【 迁移探究 1 】　在本例条件下，证明平面 BEF ⊥ 平面 ABCD . 【 迁移探究 2 】　在本例条件下，若 AB ＝ BC ，求证： BE ⊥ 平面 PAC . 证明　 连接 AC ， AC ∩ BE ＝ O . AB ∥ CD ， CD ＝ 2 AB ，且 E 为 CD 的中点 . ∴ AB 綉 CE . 又 ∵ AB ＝ BC ， ∴ 四边形 ABCE 为菱形， ∴ BE ⊥ AC . 又 ∵ PA ⊥ 平面 ABCD ，又 BE ⊂ 平面 ABCD ， ∴ PA ⊥ BE ，又 PA ∩ AC ＝ A ， PA ， AC ⊂ 平面 PAC ， ∴ BE ⊥ 平面 PAC . 探究提高　 垂直、平行关系证明中应用转化与化归思想的常见类型 . (1) 证明线面、面面平行，需转化为证明线线平行 . (2) 证明线面垂直，需转化为证明线线垂直 . (3) 证明线线垂直，需转化为证明线面垂直 . (4) 证明面面垂直，需转化为证明线面垂直，进而转化为证明线线垂直 . 热点三　平面图形中的折叠问题 【例 3 】 　 (2016· 全国 Ⅱ 卷 ) 如图，菱形 ABCD 的对角线 AC 与 BD 交于点 O ，点 E ， F 分别在 AD ， CD 上， AE ＝ CF ， EF 交 BD 于点 H ，将 △ DEF 沿 EF 折到 △ D ′ EF 的位置 . 探究提高　 1. 解决与折叠有关的问题的关键是搞清折叠前后的变化量和不变量，一般情况下，线段的长度是不变量，而位置关系往往会发生变化，抓住不变量是解决问题的突破口 . 一般地翻折后还在同一个平面上的图形的性质不发生变化，不在同一个平面上的图形的性质发生变化 . 2. 在解决问题时，要综合考虑折叠前后的图形，既要分析折叠后的图形，也要分析折叠前的图形，善于将折叠后的量放在原平面图形中进行分析求解 . 1. 空间中点、线、面的位置关系的判定 (1) 可以从线、面的概念、定理出发，学会找特例、反例 . (2) 可以借助长方体，在理解空间点、线、面位置关系的基础上，抽象出空间线、面的位置关系的定义 . 2. 垂直、平行关系的基础是线线垂直和线线平行，常用方法如下： (1) 证明线线平行常用的方法：一是利用平行公理，即证两直线同时和第三条直线平行；二是利用平行四边形进行平行转换：三是利用三角形的中位线定理证线线平行；四是利用线面平行、面面平行的性质定理进行平行转换 . (2) 证明线线垂直常用的方法： ① 利用等腰三角形底边中线即高线的性质； ② 勾股定理； ③ 线面垂直的性质：即要证两线垂直，只需证明一线垂直于另一线所在的平面即可， l ⊥ α ， a ⊂ α ⇒ l ⊥ a . 3. 解决平面图形的翻折问题，关键是抓住平面图形翻折前后的不变 “ 性 ” 与 “ 量 ” ，即两条直线的平行与垂直关系以及相关线段的长度、角度等 .