2018届二轮复习（文科数学）不等式课件（全国通用）

2018届二轮复习（文科数学）不等式课件（全国通用）

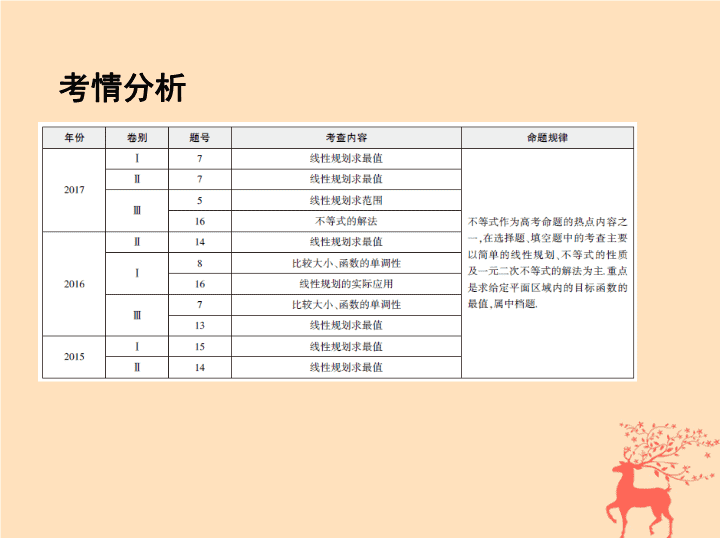
第3讲　不等式 考情分析 总纲目录 考点一  不等式的解法及应用 考点二 基本不等式及其应用 考点三 简单的线性规划问题（高频考点） 考点一  不等式的解法及应用 1.一元二次不等式的解法 把一元二次不等式先化为一般形式 ax 2 + bx + c >0( a ≠ 0),再求相应一元二 次方程 ax 2 + bx + c =0( a ≠ 0)的根,最后根据相应二次函数图象与 x 轴的位置 关系,确定一元二次不等式的解集. 2.简单分式不等式的解法 (1)   >0(<0) ⇔ f ( x ) g ( x )>0(<0); (2)   ≥ 0( ≤ 0) ⇔ f ( x ) g ( x ) ≥ 0( ≤ 0)且 g ( x ) ≠ 0. 3.指数不等式、对数不等式及抽象函数不等式,可利用函数的单调性求 解. 典型例题 (1)若函数 f ( x )=   则 f ( x ) ≥ 2的解集为   (　　) A.(- ∞ ,0] ∪ [4,+ ∞ )　    B.(- ∞ ,-1] ∪ [0,+ ∞ ) C.(- ∞ ,-1) ∪ (4,+ ∞ )　    D.(- ∞ ,-1] ∪ [4,+ ∞ ) (2)已知偶函数 f ( x )在[0,+ ∞ )上单调递减, f (2)=0.若 f ( x -1)>0,则 x 的取值范 围是 　　　     . 答案 　(1)D　(2)(-1,3) 解析 　(1)当 x ≤ 1时, 由   ≥ 2=   ,得 x ≤ -1; 当 x >1时, 由log 2 x ≥ 2=log 2 4,得 x ≥ 4. 故不等式 f ( x ) ≥ 2的解集为(- ∞ ,-1] ∪ [4,+ ∞ ). (2)∵ f (2)=0, f ( x -1)>0,∴ f ( x -1)> f (2), 又∵ f ( x )是偶函数, ∴ f (| x -1|)> f (2),又∵ f ( x )在[0,+ ∞ )上单调递减, ∴| x -1|<2,∴-2< x -1<2, ∴-1< x <3,∴ x ∈(-1,3). 不等式的求解技巧 (1)对于与函数有关的不等式,可先利用函数的单调性进行转化;(2)求解 一元二次不等式的步骤:第一步,二次项系数化为正数;第二步,解对应的 一元二次方程;第三步,若有两个不相等的实根,则利用“大于在两边,小 于夹中间”得不等式的解集;(3)含参数的不等式的求解,要对参数进行 分类讨论. 方法归纳 跟踪集训 1.设函数 f ( x )=   若 f ( x 0 )>2,则 x 0 的取值范围是   (　　) A.(- ∞ ,-1) ∪ (2,+ ∞ )　    B.(- ∞ ,-1) ∪   C.(- ∞ ,-1) ∪   　    D.(- ∞ ,-1) ∪ [2,+ ∞ ) 答案     B　不等式 f ( x 0 )>2可化为   或   解得 x 0 >   或 x 0 <-1,故选B. 2.(2017安徽合肥模拟)设函数 f ( x )=   ,则使 f ( a )+1 ≥ f ( a +1)成立的 a 的取 值范围是   (　　) A.(- ∞ ,-2)　     B.(-1,+ ∞ ) C.(- ∞ ,-2) ∪ (-1,+ ∞ )　    D.(- ∞ ,-1) 答案     C     f ( a )+1 ≥ f ( a +1) ⇔   +1 ≥   ⇔   +   ≥ 0 ⇔   ≥ 0. ∵ a 2 +3 a +4>0对一切 a ∈R恒成立, ∴原不等式等价于( a +1)( a +2)>0, ∴ a <-2或 a >-1, 故所求 a 的取值范围是(- ∞ ,-2) ∪ (-1,+ ∞ ). 考点二    基本不等式及其应用 1.三个重要不等式 (1) a , b ∈R + , a + b ≥ 2   ,当且仅当 a = b 时取等号. (2) a , b ∈R, a 2 + b 2 ≥ 2 ab ,当且仅当 a = b 时取等号. (3) a , b ∈R, ab ≤   ≤   ,当且仅当 a = b 时取等号. 2.利用基本不等式求最大值、最小值的基本法则 (1)如果 x >0, y >0, xy = p (定值),当 x = y 时, x + y 有最小值2   .(简记:积定,和有 最小值) (2)如果 x >0, y >0, x + y = s (定值),当 x = y 时, xy 有最大值   s 2 .(简记:和定,积有最 大值) 典型例题 　　(1)(2017山东,12,5分)若直线   +   =1( a >0, b >0)过点(1,2),则2 a + b 的 最小值为 　　　     . (2)(2017天津,13,5分)若 a , b ∈R, ab >0,则   的最小值为 　　　     . 答案 8 4 解析 　(1)由题设可得   +   =1,∵ a >0, b >0, ∴2 a + b =(2 a + b )   =2+   +   +2 ≥ 4+2   =8   . 故2 a + b 的最小值为8. (2)∵ a 4 +4 b 4 ≥ 2 a 2 ·2 b 2 =4 a 2 b 2 (当且仅当 a 2 =2 b 2 时“=”成立), ∴   ≥   =4 ab +   , 由于 ab >0,∴4 ab +   ≥ 2   =4   当且仅当4 ab =   时“=”成立   , 故当且仅当   时,   的最小值为4. 利用基本不等式求最值应注意的问题 (1)利用基本不等式必须注意“一正二定三相等”的原则. (2)基本不等式在解题时一般不能直接应用,而是需要根据已知条件和 基本不等式的“需求”寻找“结合点”,即把研究对象化成适用基本不 等式的形式,常见的转化方法有: ① x +   = x - a +   + a ( x > a ); ②若   +   =1,则 mx + ny =( mx + ny )·1=( mx + ny )·   = ma + nb +   +   ≥ ma + nb +2   (字母均为正数). (3)两次连用基本不等式,要注意等号取得条件的一致性. 方法归纳 跟踪集训 1.若 a , b 都是正数,则    的最小值为   (　　) A.7　    B.8　    C.9　    D.10 答案     C　∵ a , b 都是正数,∴    =5+   +   ≥ 5+2   =9, 当且仅当 b =2 a >0时取等号.故选C. 2.已知正数 x , y 满足 x 2 +2 xy -3=0,则2 x + y 的最小值是 　　　     . 答案 　3 解析 　由题意得, y =   (0< x <   ), ∴2 x + y =2 x +   =   =     ≥ 3,当且仅当 x = y =1时,等号成立. 考点三    简单的线性规划问题(高频考点) 命题点 1.求可行域的面积. 2.求目标函数的最值. 3.由最优解情况或可行域情况确定参数的值(范围). 1.平面区域的确定方法 平面区域的确定方法是“直线定界、特殊点定域”,二元一次不等式组 所表示的平面区域是各个不等式所表示的区域的交集. 2.线性目标函数 z = ax + by 最值的确定方法 线性目标函数 z = ax + by 中的 z 不是直线 ax + by = z 在 y 轴上的截距,把目标函 数化为 y =-   x +   可得   是直线 ax + by = z 在 y 轴上的截距,要根据 b 的符号确 定目标函数在什么情况下取得最大值、什么情况下取得最小值. 典型例题 　　(1)(2017课标全国Ⅲ,5,5分)设 x , y 满足约束条件   则 z = x - y 的取值范围是   (　　) A.[-3,0]　     B.[-3,2] C.[0,2]　     D.[0,3] (2)(2017湖北四校第一次联考)若变量 x , y 满足约束条件   则 z =( x -1) 2 + y 2 的最大值为   (　　) A.4　     B.   C.17　     D.16 (3)(2017江西五市部分学校第三次联考)已知实数 x , y 满足不等式组   若点 P (2 a + b ,3 a - b )在该不等式组所表示的平面区域内,则   的取值范围是   (　　) A.[-12,-7]　    B.   C.   　    D.[-12,-2] 解析 　(1)由题意,画出可行域(如图中阴影部分所示),易知 A (0,3), B (2,0). 由图可知,目标函数 z = x - y 在点 A , B 处分别取得最小值与最大值, z min =0-3= -3, z max =2-0=2,故 z = x - y 的取值范围是[-3,2].故选B.   (2) z =( x -1) 2 + y 2 表示平面区域内的点( x , y )与点 P (1,0)间距离的平方.画出约 答案 　(1)B　(2)C　(3)C 束条件所表示的平面区域如图中阴影部分所示,易知 P (1,0)与 A (2,4)间 的距离最大,因此 z max =(2-1) 2 +4 2 =17.   (3)因为点 P (2 a + b ,3 a - b )在不等式组   所表示的平面区域内,所以   即   其表示的平面区域是以 A   , B   , C   为顶点的三角形区域(包括边界).   可看作是可行域内的点 与点 M (1,-2)连线的斜率,所以 k MB ≤   ≤ k MC ,即-12 ≤   ≤ -   . 解决线性规划应注意的问题 (1)首先要找到可行域,再注意目标函数所表示的几何意义,找到目标函 数达到最值时可行域的顶点(或边界上的点),但要注意作图一定要准确, 整点问题要验证解决. (2)画可行域时应注意区域是否包含边界. (3)对目标函数 z = Ax + By 中 B 的符号,一定要注意 B 的正负与 z 的最值的对 应,要结合图形分析. 方法归纳 跟踪集训 1.(2017课标全国Ⅰ,7,5分)设 x , y 满足约束条件   则 z = x + y 的最大 值为   (　　) A.0　    B.1　    C.2　    D.3 答案     D　作出约束条件表示的可行域如图:   平移直线 x + y =0,可得目标函数 z = x + y 在 A (3,0)处取得最大值, z max =3,故选 D. 2.(2017广东惠州第三次调研)已知 x , y 满足约束条件   若 z = ax + y 的最大值为4,则 a =   (　　) A.3　    B.2　    C.-2　    D.-3 答案 　    B　作出可行域如图.   ①当 a <0时,显然 z = ax + y 的最大值不为4;②当 a =0时, z = y 在 B (1,1)处取得最 大值,为1,不符合题意;③当0< a <1时, z = ax + y 在 B (1,1)处取得最大值, z max = a +1=4,故 a =3,舍去;④当 a =1时, z = x + y 的最大值为2,不符合题意;⑤当 a >1 时, z = ax + y 在 A (2,0)处取得最大值, z max =2 a =4,得 a =2,符合题意.综上, a =2. 1.已知关于 x 的不等式( ax -1)( x +1)<0的解集是(- ∞ ,-1) ∪   ,则 a =   (　　) A.2　    B.-2　    C.-   　    D.   随堂检测 答案     B　根据一元二次不等式与其对应方程的关系知-1,-   是一元 二次方程 ax 2 +( a -1) x -1=0的两个根,所以-1 ×   = -   ,所以 a =-2,故选B. 2.(2017山东理,7,5分)若 a > b >0,且 ab =1,则下列不等式成立的是   (　　) A. a +   <   0, b >0,若不等式   -   -   ≤ 0恒成立,则 m 的最大值为   (　　) A.4　    B.16　    C.9　    D.3 答案     B　∵ a >0, b >0,∴由   -   -   ≤ 0恒成立得 m ≤   (3 a + b )= 10+   +   恒成立.∵   +   ≥ 2   =6,当且仅当 a = b 时等号成立,故1 0+   +   ≥ 16,∴ m ≤ 16,即 m 的最大值为16.故选B. 4.(2017课标全国Ⅱ,7,5分)设 x , y 满足约束条件   则 z =2 x + y 的 最小值是   (　　) A.-15　    B.-9　    C.1　    D.9 答案     A　根据线性约束条件画出可行域,如图.   作出直线 l 0 : y =-2 x .平移直线 l 0 ,当经过点 A 时,目标函数取得最小值. 由   得点 A 的坐标为(-6,-3). ∴ z min =2 × (-6)+(-3)=-15.故选A.