2018届二轮复习 三角函数的图象与性质 课件（全国通用）

2018届二轮复习 三角函数的图象与性质 课件（全国通用）

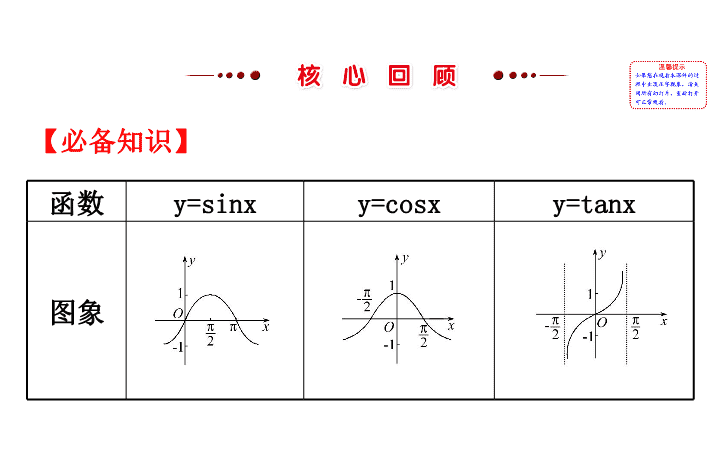
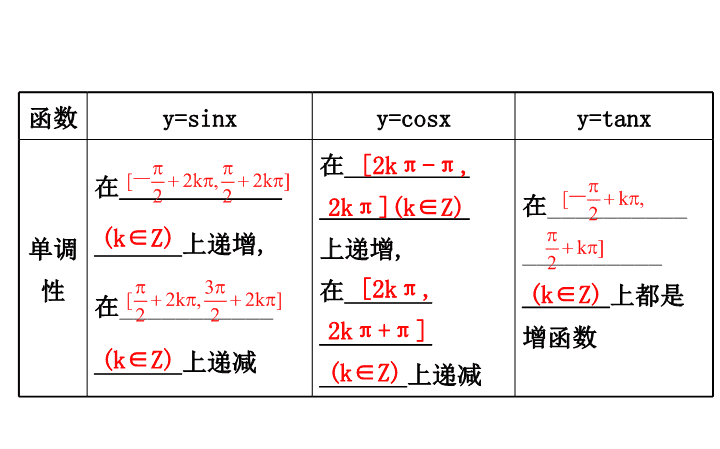
第一讲 　 三角函数的图象与性质 【 必备知识 】 函数 y=sinx y=cosx y=tanx 图象 函数 y=sinx y=cosx y=tanx 单调性 在 _____________ _______ 上递增 , 在 ___________ _______ 上递减 在 __________ ____________ 上递增 , 在 _______ _________ _______ 上递减 在 __________ __________ _______ 上都是 增函数 (k∈Z) (k∈Z) [2kπ-π, 2kπ](k∈Z) [2kπ, 2kπ+π] (k∈Z) (k∈Z) 函数 y=sinx y=cosx y=tanx 对称中 心坐标 _____________ __________ __________ 对称轴 方程 渐近线 ___________ ___________ x=_______ (k∈Z) (kπ,0),k∈Z x=kπ,k∈Z 2. 三角函数图象的两种变换方法 横坐标 横坐标 纵坐标 | φ | 纵坐标 【 真题体验 】 1.(2017 · 全国卷 Ⅲ) 设函数 f(x)= 则下列结论错误的是 ( 　　 ) A.f(x) 的一个周期为 -2π B.y=f(x) 的图象关于直线 x= 对称 C.f(x+π) 的一个零点为 x= 　 D.f(x) 在 单调递减 【 解析 】 选 D. 当 x∈ 时， x+ 函数在该区间内不单调 . 2.(2016 · 全国卷 Ⅱ) 若将函数 y=2sin2x 的图象向左平 移 个单位长度，则平移后图象的对称轴为 ( 　　 ) A.x= - (k∈Z) B.x= + (k∈Z) C.x= - (k∈Z) D.x= + (k∈Z) 【 解析 】 选 B. 平移后图象的解析式为 y=2sin2 令 2 =kπ+ ， k∈Z ， 得对称轴方程： x= + (k∈Z). 3.(2015· 全国卷 Ⅰ) 函数 f(x)=cos(ωx+ φ ) 的部分图象如图所示 , 则 f(x) 的单调递减区间为　 ( 　　 ) 【 解析 】 选 D. 由五点作图知 , 解得 ω=π, φ = , 所以 f(x)=cos , 令 2kπ<πx+ <2kπ+π,k∈Z, 解得 2k- 0) 在 上仅有 1 个最值，且为最大值，则实数 ω 的值不可能为 ( 　　 ) 【 解析 】 选 C. 依题意，函数 f(x)=sinωx+cosωx= 又函数 f(x) 在 x∈ 上仅有 1 个最 值，且为最大值，根据三角函数的图象与性质知， 当 k=0 时，经检验 ω= 时不在上面的公共区域 . 【 加练备选 】 1. 设 x,y∈R, 则 (3-4y-cosx) 2 +(4+3y+ sinx) 2 的最小值为　 ( 　　 ) A.4 B.16 　 C.5 D.25 【 解析 】 选 B.(3-4y-cosx) 2 +(4+3y+sinx) 2 =(3-4y) 2 - 2(3-4y)cosx+cos 2 x+(4+3y) 2 +2(4+3y)sinx+sin 2 x =25y 2 +2(4y-3)cosx+2(3y+4)sinx+26=25y 2 + 10 sin(x+θ)+26≥25y 2 -10 +26, 其中 tanθ= , 设 t= (t≥1), 则 z=25y 2 -10 +26=25t 2 -10t+1=(5t-1) 2 , 当 t=1 时原式取得最小值 16. 2. 已知函数 f(x)=sin 2 x-sin 2 ,x∈R, 则 f(x) 在区 间 上的最大值与最小值的和为 ________. 【 解析 】 由已知 , 有 f(x)= 因为 f(x) 在区间 上是减函数 , 在区间 上是增函数 , 所以 f(x) 在区间 上的最大值为 , 最小值为 - . 所以最大值与最小值的和为 . 答案 : 热点考向二　三角函数的性质及应用 命题解读 : 主要考查三角函数的奇偶性及对称性、周期性或求函数的单调区间 , 以及根据函数的单调性、奇偶性、周期性求参数值或取值范围 . 以选择题、填空题为主 . 【 典例 2】 (1)(2016· 全国卷 Ⅰ) 已知函数 f(x)= sin(ωx+ φ ) , 为 f(x) 的零 点 ,x= 为 y=f(x) 图象的对称轴 , 且 f(x) 在 上单调 , 则 ω 的最大值为　世纪金榜导学号 92494039 ( 　　 ) A.11 B.9 C.7 D.5 (2) 若函数 f(x)=asinωx+bcosωx(0<ω<5,ab≠0) 图 象的一条对称轴方程是 x= , 函数 f′(x) 图象的一个 对称中心是 , 则 f(x) 的最小正周期是　 ( 　　 ) A. B. C.π D.2π 【 解题导引 】 (1) 根据零点和对称轴确定 ω 的取值范围 , 再根据 f(x) 的单调性结合选项从大到小验证得答案 . (2) 根据三角函数对称中心和对称轴需要满足的等量条件列出等式 , 求出 ω, 从而求出周期 . 【 规范解答 】 (1) 选 B. 由题意知 : 则 ω=2k+1, 其中 k∈Z. 因为 f(x) 在 上单调 , 所以 接下来用排除法 . 若 ω=11, φ =- , 此时 f(x)=sin , f(x) 在 上单调递增 , 在 上单调递减 , 不 满足 f(x) 在 上单调 , 若 ω=9, φ = , 此时 f(x)=sin , 满足 f(x) 在 上单调递减 . (2) 选 C. 由 f(x)= sin(ωx+ φ ) 的对称 轴方程是 x= 可知 , +kπ(k∈Z)⇒ φ = +kπ(k∈Z), 即 =tan φ =1⇒a=b, 又 f′(x)= aωcosωx-bωsinωx 的对称中心是 , 则 f′ =0⇒aω =0⇒ω=2, 即 T= =π. 【 规律方法 】 求解三角函数的性质问题的常用方法及技巧 (1) 求单调区间的两种方法 : ① 代换法 : 求形如 y=Asin(ωx+ φ )( 或 y=Acos(ωx+ φ )) (A,ω, φ 为常数 ,A≠0,ω>0) 的单调区间时 , 令 ωx+ φ =z, 则 y=Asinz( 或 y=Acosz), 然后由复合函数的单调性求得 . ② 图象法 : 画出三角函数的图象 , 结合图象求其单调区间 . (2) 判断对称中心与对称轴 : 利用函数 y=Asin(ωx+ φ ) 的对称轴一定经过图象的最高点或最低点 , 对称中心一定是函数值等于零的点这一性质 , 通过检验 f(x 0 ) 的值进行判断 . (3) 三角函数的周期的求法 :① 定义法 .② 公式法 : y=Asin(ωx+ φ ) 和 y=Acos(ωx+ φ ) 的最小正周期为 ,y=tan(ωx+ φ ) 的最小正周期为 .③ 利用图象 . 【 变式 1+1】 1.(2017· 长沙二模 ) 已知函数 f(x)=2sin(ωx+ φ ) +1 f(α)=-1,f(β)=1, 若 |α-β| 的最小 值为 , 且 f(x) 的图象关于点 对称 , 则函数 f(x) 的单调递增区间是　 ( 　　 ) 【 解析 】 选 B. 由题设条件可知 f(x) 的周期 T=4|α- β| min =3π, 所以 ω= 又 f(x) 的图象关于点 对称 , 从而 f =1, 即 sin =0. 因为 | φ | < , 所以 φ =- , 故 f(x)=2sin +1, 再由 - +2kπ≤ +2kπ,k∈Z, 得 - +3kπ≤x≤π +3kπ,k∈Z. 2.( 新题预测 ) 函数 f(x)=sin 的图象与函数 g(x) 的图象关于 x= 对称 , 则 g(x) 具有的性质是　 ( 　　 ) A. 最大值为 1, 图象关于直线 x= 对称 B. 在 上单调递减 , 为奇函数 C. 在 上单调递增 , 为偶函数 D. 周期为 π, 图象关于点 对称 【 解析 】 选 B. 由题意得 ,g(x)= = sin(-2x)=-sin2x, 最大值为 1, 而 g =0, 图象不关于 直线 x= 对称 , 故 A 错误 ; 当 x∈ 时 ,2x∈ , 满 足单调递减 , 显然 g(x) 也是奇函数 , 故 B 正确 ,C 错误 ; 周 期 T= 故图象不关于点 对称 , 故 D 错误 . 3.( 新题预测 ) 下列函数是以 π 为最小正周期的偶函数的是　 ( 　　 ) A.y=sin|x| B.y=|cos2x| C.y=|sin2x| D.y=|tanx| 【 解析 】 选 D.A 是偶函数但不具有周期性 ;B 是偶函数 , 但最小正周期是 ;C 是偶函数 , 但最小正周期是 ;D 以 π 为最小正周期且是偶函数 . 【 加练备选 】 (2017· 石家庄二模 ) 已知函数 f(x)= sinωx+cosωx(ω>0),x∈R. 若函数 f(x) 在区间 (-ω,ω) 内单调递增 , 且函数 y=f(x) 的图象关于直线 x=ω 对称 , 则 ω 的值为 __________. 【 解析 】 f(x)=sinωx+cosωx= 因为 f(x) 在区间 (-ω,ω) 内单调递增 , 且函数图象关 于直线 x=ω 对称 , 所以 f(ω) 必为一个周期上的最大值 , 所以有 ω · ω+ =2kπ+ ,k∈Z, 所以 ω 2 = +2kπ,k∈Z. 又 ω-(-ω)≤ , 即 ω 2 ≤ , 所以 ω 2 = , 所以 ω= . 答案 : 热点考向三　三角函数的图象及应用 类型一 三角函数的图象变换及应用 【 典例 3】 (1)(2017· 佛山二模 ) 若将函数 f(x)= cos 的图象向左平移 φ ( φ >0) 个单位 , 所得图 象关于原点对称 , 则 φ 最小时 ,tan φ = 　 ( 　　 ) (2)(2017· 全国卷 Ⅰ) 已知曲线 C 1 :y=cosx,C 2 :y = sin , 则下面结论正确的是　 ( 　　 ) 世纪金榜导学号 92494040 A. 把 C 1 上各点的横坐标伸长到原来的 2 倍 , 纵坐标不变 , 再把得到的曲线向右平移 个单位长度 , 得到曲线 C 2 B. 把 C 1 上各点的横坐标伸长到原来的 2 倍 , 纵坐标不变 , 再把得到的曲线向左平移 个单位长度 , 得到曲线 C 2 C. 把 C 1 上各点的横坐标缩短到原来的 倍 , 纵坐标不 变 , 再把得到的曲线向右平移 个单位长度 , 得到曲 线 C 2 D. 把 C 1 上各点的横坐标缩短到原来的 倍 , 纵坐标不 变 , 再把得到的曲线向左平移 个单位长度 , 得到曲 线 C 2 【 解题导引 】 (1) 利用平移变换结合奇函数求解 . (2) 首先把曲线 C 1 ,C 2 统一为同一三角函数名 , 可将 C 1 :y=cosx 用诱导公式处理 ,y=cosx= 再进行变换即可 . 【 规范解答 】 (1) 选 B. 函数向左平移后得到 y= cos , 其图象关于原点对称 , 为奇函数 , 故 2 φ + ， k∈Z, 即 (2) 选 D.C 1 :y=cosx,C 2 :y= , 首先把曲线 C 1 ,C 2 统一为同一三角函数名 , 可将 C 1 :y= cosx 用诱导公式处理 . y=cosx= 横坐标变换需将 ω=1 变成 ω=2, 即 y=sin 注意 ω 的系数 , 在左右平移时需将 ω=2 提到括号外面 , 这时 x+ 平移至 x+ , 根据 “ 左加右减 ” 原则 , “ x+ ” 到 “ x+ ” 需加上 , 即再向左平移 . 【 母题变式 】 1. 若例 (1) 中的函数 f(x) 的图象向左平移 φ 个单位 , 得 到函数 y=g(x) 的图象 , 其中锐角 φ 的终边经过点 P(m, ), 且 cos φ = , 则函数 y=g(x) 的图象的对称中心 是 ________. 【 解析 】 cos φ = 又 φ 为锐角 , 所以 m=1, φ = , 所以 g(x)=cos , 所以 2x+ =k π + ,k ∈ Z ⇒ x= k ∈ Z. 答案 : ,k∈Z 2. 若例 (1) 中将函数 f(x) 图象上的点 P 向右平移 m(m>0) 个单位得到点 P′, 若 P′ 位于函数 y=cos2x 的 图象上 , 则 m 的最小值为 ________. 【 解析 】 由题可知 t= 点 P′ 的坐标为 , 因为点 P′ 位于函数 y=cos2x 的 图象上 , 所以 所以 +2m=2kπ+ 或 2kπ+ (k∈Z), 解得 m=kπ+ 或 kπ+ (k∈Z), 又 m>0, 所以当 k=0 时 ,m 取得最小值 , 且最小值 为 . 答案 : 类型二 三角函数的图象及解析式的综合应用 【 典例 4】 (1) 函数 f(x)=sin(πx+θ) 的部分 图象如图 , 且 f(0)=- , 则图中 m 的值为　 ( 　　 ) (2) 已知向量 m =(2sinωx,sinωx), n =(cosωx, -2 sinωx)(ω>0), 函数 f(x)= m · n + , 直线 x=x 1 , x=x 2 是函数 y=f(x) 的图象的任意两条对称轴 , 且 |x 1 - x 2 | 的最小值为 . 世纪金榜导学号 92494041 ① 求 ω 的值 ; ② 求函数 f(x) 的单调递增区间 ; ③ 若 f(α)= , 求 sin 的值 . 【 解题导引 】 (1) 根据图象的特点求值 . (2)① 由向量数量积写出解析式 , 根据对称轴确定周期 , 进一步确定参数 ω; ② 根据正弦函数的单调性求出单调区间 ; ③ 根据诱导公式及倍角公式求函数值 . 【 规范解答 】 (1) 选 B.f(0)=sinθ=- , 又 |θ|< , 所以 θ=- , 所以 由图象可知 , mπ- (2)① 已知向量 m =(2sinωx,sinωx), n =(cosωx, -2 sinωx)(ω>0), 所以函数 f(x)= m · n + =2sinωx · cosωx+sinωx(-2 sinωx)+ =sin2ωx-2 sin 2 ωx+ =sin2ωx+ cos2ωx =2sin 因为直线 x=x 1 ,x=x 2 是函数 y=f(x) 的图象的任意两条 对称轴 , 且 |x 1 -x 2 | 的最小值为 , 所以函数 f(x) 的最 小正周期为 ×2=π, 即 =π, 得 ω=1; ② 由①知 ,f(x)=2sin , 令 2kπ- ≤2x+ ≤ 2kπ+ (k∈Z), 解得 kπ- ≤x≤kπ+ (k∈Z), 所以函数 f(x) 的单调递增区间为 k∈Z; ③ 由已知条件 , 得 f(α)= 所以 所以 cos 所以 【 规律方法 】 1. 函数表达式 y=Asin(ωx+ φ )+B 的确定方法 字母 确定途径 说　　明 A 由最值确定 A= B 由最值确定 B= 字母 确定途径 说　　明 ω 由函数的 周期确定 利用图象中最高、最低点 , 与 x 轴交点的横坐标确定周期 φ 由图象上的特殊点确定 代入图象上某一个已知点的坐标 , 表示出 φ 后 , 利用已知范围求 φ 2. 三角函数图象平移问题处理策略 (1) 看平移要求 : 首先要看题目要求由哪个函数平移得到哪个函数 , 这是判断移动方向的关键点 . (2) 看移动方向 : 移动的方向一般记为“正向左 , 负向右” , 看 y=Asin(ωx+ φ ) 中 φ 的正负和它的平移要求 . (3) 看移动单位 : 在函数 y=Asin(ωx+ φ ) 中 , 周期变换 和相位变换都是沿 x 轴方向的 , 所以 ω 和 φ 之间有一定 的关系 , φ 是初相 , 再经过 ω 的压缩 , 最后移动的单位 是 . 【 通关 1+1】 1.(2017· 衡水一模 ) 如图是函数 f(x)=Asin(2x+ φ ) 图象的一部分 , 对不同的 x 1 ,x 2 ∈[a,b], 若 f(x 1 )=f(x 2 ), 有 f(x 1 +x 2 )= , 则　 ( 　　 ) 世纪金榜导学号 92494042 A.f(x) 在区间 内单调递增 B.f(x) 在区间 内单调递减 C.f(x) 在区间 内单调递增 D.f(x) 在区间 内单调递减 【 解析 】 选 A. 根据图象得出 :A=2, 对称轴方程为 x= , 所以 2sin(x 1 +x 2 + φ )=2⇒x 1 +x 2 + φ = , 所以 x 1 +x 2 = - φ , 因为 f(x 1 +x 2 )= , 所以 2sin 即 sin(π- φ )= , 因为 | φ |≤ , 所以 φ = , 所以 f(x)=2sin , 因 为 k∈Z, 所以 - +kπ≤x ≤ +kπ,k∈Z, 即为 f(x) 的单调递增区间 . 2.( 新题预测 ) 将函数 g(x)= 的图象 上各点的横坐标伸长为原来的 2 倍 ( 纵坐标不变 ) 后得 到 h(x) 的图象 , 设 f(x)= x 2 +h(x), 则 f′(x) 的图象 大致为　 ( 　　 ) 【 解析 】 选 A. 因为 g(x)= =cos2x, 所以 h(x)=cosx, 所以 f(x)= x 2 +cosx, 可得 :f′(x)= x-sinx, 显然 f′(x) 为奇函数 , 排除 B,D, 又当 x= 时 , >0, 结合选项中函数的 图象 , 排除 C. 【 加练备选 】 (2017· 福州一模 ) 已知函数 f(x)= Asin(ωx+ φ )(A>0,ω>0,0< φ <π) 的部分图象如图 所示 , 则 f(x) 的单调递减区间为　 ( 　　 ) A.[8k+1,8k+5](k∈Z) B.[8k-1,8k+5](k∈Z) C.[8k-5,8k+1](k∈Z) D.[8k+3,8k+5](k∈Z) 【 解析 】 选 A. 由图象可知 A=2,T=2×(7-3)=8, 又由 =8 得 ω= , 所以 f(x)=2sin , 又 0< φ < π, 结合 f(3)=0, 即 2sin =0, 得 φ = , 故 f(x)= 2sin , 由 (k∈Z) 得 8k+1≤x≤8k+5(k∈Z). 故函数 f(x) 的单调递减区间 为 [8k+1,8k+5](k∈Z).