- 2021-06-24 发布 |
- 37.5 KB |
- 16页


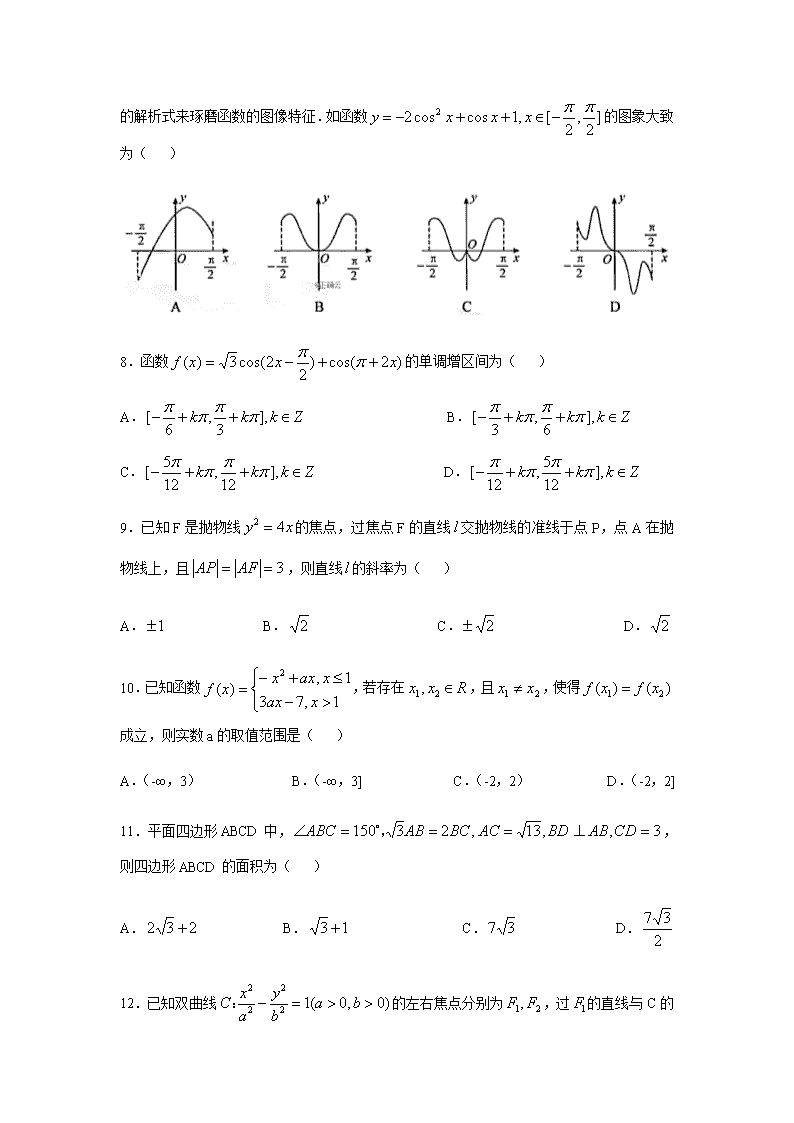
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
湖北省荆州市公安县第三中学2020届高三下学期4月线上调研考试数学(文)试卷
文科数学试卷 本试卷共5页,23题(含选考题)。全卷满分150分。考试用时120分钟。 注意事项: 1.考试过程中,请考生自觉遵守考试纪律等相关规定,诚信应考,不得有作弊、泄露试题等行为。请家长做好监考工作。 2.请确保网络环境、考试环境良好,备好答题所用的白纸和笔。 3.登录好分数APP,点击“作业测试”,进入对应考试科目。“试卷”将根据考试时间准时显示。开考后:考生首先在白纸上手写答题。答题结束后点击“填写答题卡”,进入到“在线答题卡”。将事先准备好的答案,填写至在线答题卡上(选择题、多选题及判断题,直接在“在线答题卡”上勾选答案;主观题按照要求将手写的答案竖向拍照,并分别上传),然后点击“提交答题卡” 完成提交。答题卡上传提交后考试时间范围内还能继续提交覆盖,为了避免大家都在考试最后快结束的时间上传造成拥堵,建议提前上传。 备注:主观题要确保答案及照片清晰,干净、完整;为留取拍照时间,考试将延长10分钟。 4.此次全省联考是检测复课前线上备考成效的一次重要考试,有利于调整和优化复课后备考策略,请考生和家长高度重视。考试结束后,考试组织方将为所有考生免费提供《考试成绩和学情分析报告》。请考生或家长及时扫描右方二维码,关注“育路通”微信公众号。依次点击“高考测评一查看报告”,即可免费查询。 一、选择题:本大题共 12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合,集合,则A∩B=( ) A. B. C. D. 2.已知,其中i为虚数单位,则复数 在复平面内对应的点在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 3.已知,则( ) A.y<x<z B.y<z<x C.z<x<y D.z<y<x 4.已知平面向量均为单位向量,若向量的夹角为,则=( ) A.37 B.25 C. D.5 5.若不等式,对恒成立,则实数m的最大值为( ) A.7 B.8 C.9 D.10 6.某城市在进行创建文明城市的活动中,为了解居民对“创建文明城”的满意程度,组织居民给活动打分(分数为整数,满分100分),从中随机抽取一个容量为120的样本,发现所给数据均在[40,100]内.现将这些分数分成以下6组并画出样本的频率分布直方图,但不小心污损了部分图形,如图所示.观察图形则下列说法中有错误的是( ) A.第三组的频数为18人 B.根据频率分布直方图估计众数为75分 C.根据频率分布直方图估计样本的平均数为75分 D.根据频率分布直方图估计样本的中位数为75分 7.我国著名数学家华罗庚先生曾说:“数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.”在数学的学习和研究中,常用函数的图像研究函数的性质,也常用函数的解析式来琢磨函数的图像特征.如函数的图象大致为( ) 8.函数的单调增区间为( ) A. B. C. D. 9.已知F是抛物线的焦点,过焦点F的直线交抛物线的准线于点P,点A在抛物线上,且,则直线的斜率为( ) A. B. C. D. 10.已知函数,若存在,且,使得成立,则实数a的取值范围是( ) A.(-∞,3) B.(-∞,3] C.(-2,2) D.(-2,2] 11.平面四边形ABCD中,,则四边形ABCD的面积为( ) A. B. C. D. 12.已知双曲线的左右焦点分别为,过 的直线与C的两条渐近线分别交于A、B两点,若以为直径的圆过点B,且A为的中点,则C的离心率为( ) A. B.2 C. D. 二、填空题:本大题共4小题,每小题5分,共20分. 13.设曲线y=ex+1上点P处的切线平行于直线,则点P的坐标是 . 14.已知为锐角,且,则tan = . 15.已知A,B,C是球O球面上的三点,AC=BC=6,AB=,且四面体OABC的体积为24.则球O的表面积为 . 16.自湖北爆发新型冠状病毒肺炎疫情以来湖北某市医护人员和医疗、生活物资严重匮乏,全国各地纷纷驰援.某运输队接到从武汉送往该市物资的任务,该运输队有8辆载重为6t的A型卡车,6辆载重为10t的B型卡车,10名驾驶员,要求此运输队每天至少运送240t物资.已知每辆卡车每天往返的次数为A型卡车5次,B型卡车4次,每辆卡车每天往返的成本A型卡车1200元,B型卡车1800元,则每天派出运输队所花的成本最低为 . 三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17题~第21题为必考题,每个试题考生都必须作答.第22题~第23题为选考题,考生根据要求作答. (一)必考题:共 60分. 17.(本小题满分12分) 已知函数的图像经过点A(2,1)和B(5,2),. (1)求; (2)设数列的前n项和为S n ,,求的前n项和T n . 18.(本小题满分12分) 2020年春节期间,新型冠状病毒(2019-nCoV)疫情牵动每一个中国人的心,危难时刻全国人民众志成城.共克时艰,为疫区助力.我国S省Q市共100家商家及个人为缓解湖北省抗疫消毒物资压力,募捐价值百万的物资对口输送湖北省H市. (1)现对100家商家抽取5家,其中2家来自A地,3家来自B地,从选中的这5家中,选出3家进行调研.求选出3家中1家来自A地,2家来自B地的概率. (2)该市一商家考虑增加先进生产技术投入,该商家欲预测先进生产技术投入为49千元的月产增量.现用以往的先进技术投入(千元)与月产增量(千件)(i=1,2,3,…,8)的数据绘制散点图,由散点图的样本点分布,可以认为样本点集中在曲线的附近,且:,,,,,其中,,,根据所给的统计量,求y关于x回归方程,并预测先进生产技术投入为49千元时的月产增量. 附:对于一组数据,其回归直线 的斜率和截距的最小二乘法估计分别为 19.(本小题满分12分) 如图,在四棱锥S -ABCD中,侧面SCD为钝角三角形且垂直于底面ABCD,CD =SD,点M是SA的中点,AD// BC,∠ABC =90°,AB =AD=BC=a. (1)求证:平面MBD⊥平面SCD; (2)若∠SDC=120°,求三棱锥C—MBD的体积 20.(本小题满分12分) 已知椭圆: (a>b>0)过点E(,1),其左、右顶点分别为A,B,左、右焦点为F1,F2,其中F1(,0). (1)求栖圆C的方程: (2)设M(x0,y0)为椭圆C上异于A,B两点的任意一点,MN⊥AB于点N,直线,设过点A与x轴垂直的直线与直线l交于点P,证明:直线BP经过线段MN的中点. 21.(本小题满分12分) 已知函数 (1)求函数f(x)的奇偶性.并证明当时函数f(x)只有一个极值点; (2)当时,求f(x)的最小值; (二)选考题:共10分.请考生在22,23题中任选一题作答.如果多做,则按所做的第一题计分.作答时写清题号. 22.[选修4-4:坐标系与参数方程](10分) 在平面直角坐标系xOy中,曲线的参数方程为(θ为参数),以原点为极点,x轴非负半轴为极轴,建立极坐标系,曲线的极坐标方程为. (1)求曲线的极坐标方程以及曲线的直角坐标方程; (2)若直线与曲线、曲线在第一象限交于P、Q,且,点M的直角坐标为,求的面积. 23.[选修4-5:不等式选讲](10分) 已知实数a,b满足. (1)求的取值范围; (2)若ab>0,求证:.查看更多