- 2021-06-24 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020届二轮复习数列(一)学案(全国通用)
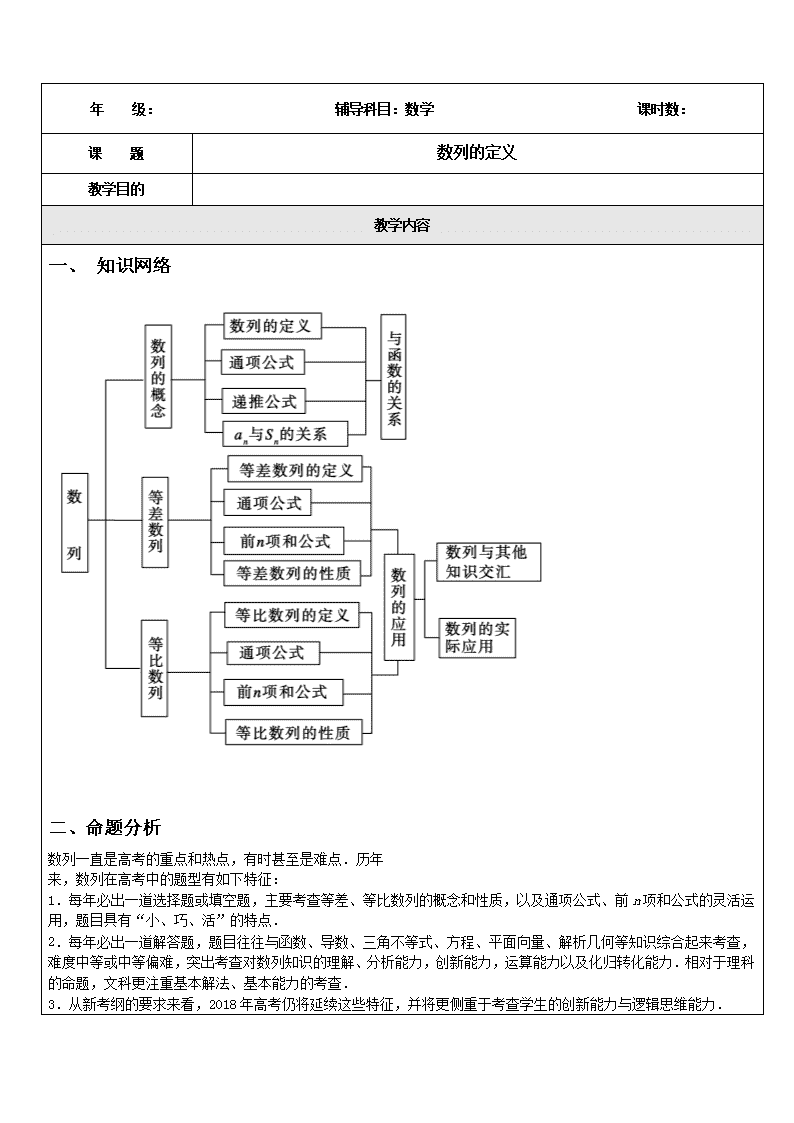
年 级: 辅导科目:数学 课时数: 课 题 数列的定义 教学目的 教学内容 一、 知识网络 二、命题分析 数列一直是高考的重点和热点,有时甚至是难点.历年 来,数列在高考中的题型有如下特征: 1.每年必出一道选择题或填空题,主要考查等差、等比数列的概念和性质,以及通项公式、前n项和公式的灵活运用,题目具有“小、巧、活”的特点. 2.每年必出一道解答题,题目往往与函数、导数、三角不等式、方程、平面向量、解析几何等知识综合起来考查,难度中等或中等偏难,突出考查对数列知识的理解、分析能力,创新能力,运算能力以及化归转化能力.相对于理科的命题,文科更注重基本解法、基本能力的考查. 3.从新考纲的要求来看,2018年高考仍将延续这些特征,并将更侧重于考查学生的创新能力与逻辑思维能力. 三、复习建议 针对新课标考试“强调基础,淡化技巧,提高能力”的特征,复习本单元时应注意以下几点: 1.重视对等差数列、等比数列的概念的理解,掌握它们的通项公式,前n项和公式及其性质. 2.重视运算能力的提高,涉及的解不等式、解方程问题以及等式的相加减、相乘除等运算,力求熟练而准确. 3.重视知识的综合,深刻领悟蕴藏在数列概念及方法中的数学思想,对其中的函数与方程、数形结合、分类讨论、等价转化等数学思想要在解题中进行感受和体会. 四、知识讲解 第一节 数列的概念与简单表示法 (一)高考目标 考纲解读 1.了解数列的概念和几种简单的表示方法(列表、图像、通项公式). 2.了解数列是自变量为正整数的一类函数. 考向预测 1.已知数列的通项公式或递推关系,求数列的各项. 2.以数列的前几项为背景,考查“归纳—推理”思想. 3.由数列的递推关系式求数列的通项公式的是本节重点,也是本节难点. (二)课前自主预习 知识梳理 1.数列的定义 按照 排成的一列数称为数列,数列中的每一个数叫做这个数列的 排在第一位的数称为这个数列的第1项(通常也叫做 ). 2.数列与函数的关系 在函数意义下,数列是定义域为N+(或它的 )的函数,f(n)是当自变量n从1开始依次取 时所对应的一列 f(1),f(2),…,f(n)……通常用an代替f(n),故数列的一般形式为 ,简记为{an},其中an是数列的第 项. 3.数列的分类 分类 原则 类型 满足条件 项数 有穷数列 项数 无穷数列 项数 项与项间的大小关系 递增数列 其中n∈N* 递减数列 常数列 an+1=an 其他 摆动数列 从第2 标准 项起,有些项大于它的前一项,有些项小于它的前一项 4.数列的表示法 (1)数列的一般形式可以写成: (2)数列的表示法分别为 、 5.数列的通项公式 如果数列{an}的第n项an与 之间的关系可以用一个式子来表示,那么这个公式叫做这个数列的通项公式. 6.数列的递推公式 若一个数列首项确定,其余各项用an与an-1的关系式表示(如an=2an-1+1,n>1),则这个关系式就称为数列的递推公式. (三)基础自测 1.(2018·安徽文)设数列{ɑn}的前n项和Sn=n2,则a8的值为( ) A.15 B.16 C.49 D.64 [答案] A [解析] a8=S8-S7=64-49=15,a8=15. 2.数列,-,,-,…的一个通项公式是( ) A.an=(-1)n+1 B.an=(-1)n C.an=(-1)n+1 D.an=(-1)n [答案] C 3.若数列{an}(n∈N*)的首项为14,前n项的和为Sn,点(an,an+1)在直线x-y-2=0上,那么下列说法正确的是( ) A.当且仅当n=1时,Sn最小 B.当且仅当n=8时,Sn最大 C.当且仅当n=7或8时,Sn最大 D.Sn有最小值,无最大值 [答案] C [解析] 由题意得:an-an+1-2=0,则an+1-an=-2,所以数列{an}是以a1=14,d=-2的等差数列, 则Sn=14n+×(-2)=-n2+15n,所以当且仅当n=7或8时,Sn最大. 4.数列{an}的前n项和为Sn,若an=,则S5等于( ) A.1 B. C. D. [答案] B [解析] S5=++…+ =++…+=1-=. 5.将全体正整数排成一个三角形数阵: 1 2 3 4 5 6 7 8 9 10 … … … … … … … 按照以上排列的规律,第n行(n≥3)从左向右的第3个数为________. [解析] 前n-1行共有正整数1+2+…+(n-1)个,即个,因此第n行第3个数是全体正整数中 第+3个,即为. [答案] 6.已知数列{an}的首项a1=,且满足=+5(n∈N*),则a2018=________. [答案] [解析] 由-=5知,数列是以=3为首项,以5为公差的等差数列, 故=+2018d=3+10055=10058. 7.写出分别满足下列条件的数列的前4项,并归纳出通项公式: (1)a1=0,an+1=an+(2n-1)(n∈N+); (2)a1=3,an+1=3an(n∈N+). [解析] (1)由条件得a1=0,a2=0+1=1=12, a3=1+(2×2-1)=4=22,a4=4+(2×3-1)=9=32,归纳通项公式为an=(n-1)2. (2)由条件得a1=3,a2=3a1=32,a3=3a2=33,a4=3a3=34,归纳通项公式为an=3n. (四)典型例题 1.命题方向:有数列的前几项探索数列的通项公式 [例1] 根据数列的前几项,写出下列各数列的一个通项公式: (1),,,,…; (2)1,3,6,10,15,…; (3),,-,,-,,…; (4)3,33,333,3333,…. [分析] 先观察各项的特点,然后归纳出其通项公式,要注意项与项数的关系及项与前后项之间的联系. [解析] (1)注意到前四项中两项分子均为4,不妨把分子都统一为4,即,,,,…, 因而有an=. (2)注意到6=2×3,10=2×5,15=3×5,规律还不明显,再把各项同乘以2,即,,,,,…,因而有an=. (3)各项的分母分别为21,22,23,24,…易看出第2,3,4项的分子分别比分母少3,因此把第1项变为-, 至此原数列已化为-,,-,,…,∴an=(-1)n·. (4)将数列各项改写为:,,,,…,分母都是3,而分子分别是10-1,102-1,103-1,104-1,…, ∴an=(10n-1). [点评] 根据数列的前几项写出数列的一个通项公式,解决这一问题的关键是通过观察、分析、比较去发现项与项之间的关系.如果关系不明显,可将项适当变形,让规律突显出来以便于找出通项公式. 跟踪练习1: 根据下面各数列的前几项的值,写出数列的一个通项公式: (1)1,,,,,… (2)-,,-,,-,,… (3),,,,,…; (4),-1,,-,,-,…. (5)1,3,7,15,31,… [解析] (1)将数列写成: ,,,,,… 观察分子、分母与项数n之间的联系,易知: 其通项公式为an=. (2)这是一个与(-1)n有关的数列,可将数列写成 -,,-,,-,,… 可知分母组成以3为公差的等差数列,分子为以3为首项,1为公差的等差数列,因此其通项公式为: an=(-1)n. (3)每一项的分子比分母少1,而分母组成数列21,22,23,24,…,所以an=. (4)偶数项为负,奇数项为正,故通项公式必含因子(-1)n+1,观察各项绝对值组成的数列,从第3项到第6项可见,分母分别由奇数7,9,11,13组成,而分子则是32+1,42+1,52+1,62 +1,按照这样的规律第1、2两项可改写为,-,所以an=(-1)n+1·. (5)考虑数列的差分数列{an+1-an}. a2-a1=2 a3-a2=4, a4-a3=8, …… an-=2n-1.(n≥2) 将这n-1个式子累加,得 an-=2+22+23+…+2n-1=2n-2 (n≥2) ∴ an=+2n-2=1+2n-2=2n-1. (n≥2) 当n=1时,此式仍成立,故所求通项公式为an=2n-1. [点评] 根据数列的前几项写通项时,所求的通项公式不是惟一的.其中常用方法是观察法.观察an与n之间的联系,用归纳法写出一个通项公式,体现了由特殊到一般的思维规律.联想与转换是有效的思维方法,它是由已知认识未知、将未知转化为已知的重要思维方法. 2.命题方向:由与的关系求通项 [例2] 已知数列{an}的前n项和为Sn,Sn=(an-1)(n∈N*). (1)求a1,a2,a3的值; (2)求an的通项公式及S10. [解析] (1)由a1=S1=(a1-1)得a1=-. 又a1+a2=S2=(a2-1),解得a2=.同理a3=- (2)n≥2时,an=Sn-Sn-1=(an-1)-(an-1-1), 得=-. ∴数列{an}是首项为-,公比为-的等比数列.即an=(-)n,∴S10==. (2)n≥2时,an=Sn-Sn-1=(an-1)-(an-1-1),得=-. ∴数列{an}是首项为-,公比为-的等比数列.即an=(-)n,∴S10==. [点评] 数列的通项an与前n项和Sn的关系是: an=. 此公式经常使用,应引起重视.当n=1时,a1若适合Sn-Sn-1,则n=1的情况可并入n≥2时的通项an;当n=1时,a1若不适合Sn-Sn-1,则用分段函数的形式表示. 跟踪练习2: 已知数列{an}的前n项和Sn,求{an}的通项公式.(1)Sn=2n2-3n;(2)Sn=3n+b. [解析] 利用数列的通项an与前n项和Sn的关系 an=. 解 (1)当n=1时,a1=S1=-1, 当n≥2时,an=Sn-Sn-1=4n-5. 又∵a1=-1,适合,an=4n-5, ∴an=4n-5. (2)当n=1时,a1=S1=3+b. n≥2时,an=Sn-Sn-1=2·3n-1, 因此,当b=-1时,a1=2适合an=2·3n-1, ∴an=2·3n-1. 当b≠-1时,a1=3+b不合适an=2·3n-1, ∴an=. 综上可知,当b=-1时,an=2·3n-1; 当b≠-1时,an= 3.命题方向:根据递推公式求通项公式 [例3] 根据下列条件,写出数列的通项公式. (1)a1=2,an+1=an+n;(2)a1=1,2n-1an=an-1. [分析] (1)将递推关系写成n-1个等式累加. (2)将递推关系写成n-1个等式累乘,或逐项迭代也可. [解析] (1)当n=1,2,3,…,n-1时,可得n-1个等式: an-an-1=n-1,an-1-an-2=n-2,…,a2-a1=1, 将其相加,得an-a1=1+2+3+…+(n-1), ∴an=a1+=2+=. (2)方法一:∵an=···…···a1=n-1·n-2·…·2·1·a1 =1+2+…+(n-1)=, ∴an=. 方法二:由2n-1an=an-1得an=n-1an-1 ∴an=n-1an-1=n-1·n-2an-2=…=n-1·n-2·…·1a1=(n-1)+(n-2)+…+2+1=. [点评] 1.已知a1且an-an-1=f(n)(n≥2),可以用“累加法”,即an-an-1=f(n),an-1-an-2=f(n-1),…,a3-a2=f(3),a2-a1=f(2). 所有等式左右两边分别相加,代入a1得an. 2.已知a1且=f(n)(n≥2),可以用“累乘法”, 即=f(n),=f(n-1),…,=f(3),=f(2),所有等式左右两边分别相乘,代入a1得an. 提醒:并不是每一个数列都有通项公式,如果一个数列有通项公式,那么它的通项公式在形式上也可以不止一个. 跟踪练习3: 根据下列各个数列{an}的首项和基本关系式,求其通项公式. (1)a1=1,an=an-1+3n-1(n≥2); (2)a1=1,an=an-1(n≥2). [解析] (1)∵an=an-1+3n-1, ∴an-an-1=3n-1, an-1-an-2=3n-2, an-2-an-3=3n-3, … a2-a1=31. 以上n-1个等式两边分别相加得 an=a1+31+32+…+3n-1=1+3+32+…+3n-1=. a2=a1. 以上n-1个式子等式两边分别相乘得an=a1···…·==. 4.命题方向:函数与方程思想在数列中的应用 [例4] 已知数列{an}的通项公式an=(n+1)·()n,求n为何值时,an取最大值. [分析] 已知数列{an}的通项公式,要求n为何值时an取最大值,则需满足.因为涉及an-1,所以应先讨论a1是否为最大值,然后再由不等式组去求使an最大时n的取值. [解析] 易知a1不是数列{an}中的最大的项, ∴an若取最大值应满足(n≥2), 由已知中an=(n+1)·()n,则有 an-an+1=(n+1)·()n-(n+2)·()n+1=()n·[n+1-(n+2)]=()n·. 由an-an+1≥0,即()n·≥0, 解不等式,得n≥8; an-an-1=(n+1)·()n-(n-1+1)·()n-1=()n-1·[(n+1)·-n]=()n-1·, 当an-an-1≥0,即()n-1·≥0, 解不等式,得n≤9; ∴同时满足不等式组的正整数n的取值只能是8,9, 又a8=9×()8,a9=10×()9, 即a8=a9=. ∴当n=8或n=9时,a8=a9两项都是数列{an}中的最大项. [点评] 数列是特殊的函数,因此数列中一些问题的研究与函数有一定的联系.如:数列中的最大、最小项问题;数列的单调性问题等都可以借助于函数知识研究,当然也有差别.高考对本考点的考查主要以选择、填空的形式出现,有时也出现在解答题的某一问中,主要同函数、不等式等内容结合,结合性较强,有一定的难度.备考中应从函数的角度把握数列中最大、最小项的求法以及数列单调性的判断方法. 跟踪练习4: 已知函数f(x)=,数列{an}满足f()=-2n. (1)求数列{an}的通项公式; (2)求证:数列{an}是递减数列. [解析] (1)解:f(x)=, ∴f(log2an)=2log2an-2-log2an=an-, ∴an-=-2n,∴an2+2n·an-1=0. 又an>0,∴an=-n. (2)证明:∵an>0,且an=-n, ∴==<1. ∴an+1查看更多