2020届二轮复习数列极限与函数极限学案（全国通用）

2020届二轮复习数列极限与函数极限学案（全国通用）

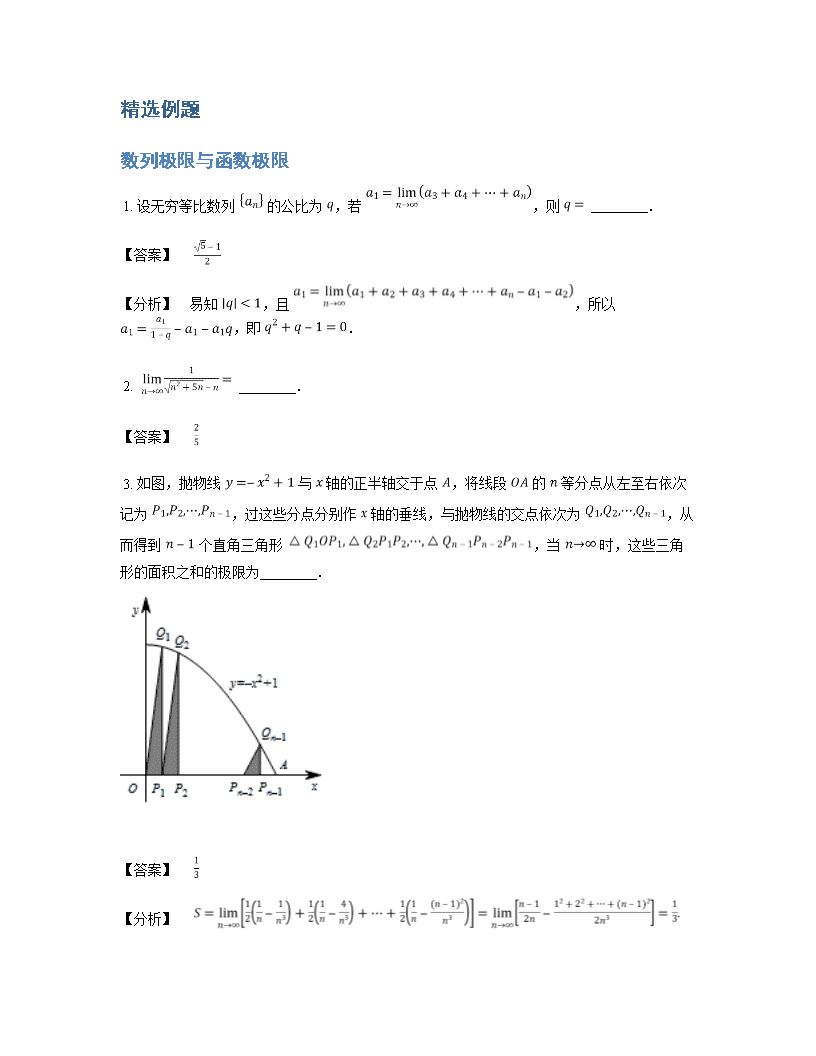
· ‎2020届二轮复习 数列极限与函数极限 学案（全国通用）‎ · 数列极限 设 为实数数列， 为常数．若对任意给定的正数 ，总存在正整数 ，使得当 时，有 ，则称数列 收敛于 ，常数 称为数列 的极限．并记作 ‎ 读作 “ 当 趋于无穷大时， 的极限等于 ”．若数列 没有极限，则称 不收敛，或称 为发散数列​​​．对于收敛数列有以下两个基本性质，即收敛数列的唯一性和有界性：定理1：如果数列 ​​ 收敛，则其极限是唯一的；定理2：如果数列 收敛，则其一定是有界的，即对于一切 ​​，总可以找到一个正数 ，使得 ．​‎ · 函数极限 函数极限可以分成 三种． 设函数 在点 的某一去心邻域，即 内有定义，如果存在常数 ，对于任意给定的正数 （无论它多么小），总存在正数 ，使得当 满足不等式 时，对应的函数值 都满足不等式 ，那么常数 就叫做函数 当 时的极限，记作 ‎ ‎ ​设 为定义在 上的函数， 为常数．若对于任意给定的正数 ​，存在正数 ，使得当 时，有 ，则称函数 当 趋于正无穷时以 为极限，记作 ‎ 与此类似．​​‎ 精选例题 数列极限与函数极限 ‎ 1. 设无穷等比数列 的公比为 ，若 ，则  ．‎ ‎【答案】     ‎ ‎【分析】    易知 ，且 ，所以 ，即 ．‎ ‎ 2.  ．‎ ‎【答案】     ‎ ‎ 3. 如图，抛物线 与 轴的正半轴交于点 ，将线段 的 等分点从左至右依次记为 ，过这些分点分别作 轴的垂线，与抛物线的交点依次为 ，从而得到 个直角三角形 ，当 时，这些三角形的面积之和的极限为  ．‎ ‎【答案】     ‎ ‎【分析】     ‎ ‎ 4. 计算：  ．‎ ‎【答案】     ‎ ‎ 5.  ．‎ ‎【答案】     ‎ ‎ 6. ，则常数  ．‎ ‎【答案】     ‎ ‎ 7.  ．‎ ‎【答案】     ‎ ‎ 8.  ．‎ ‎【答案】     ‎ ‎ 9.  ．‎ ‎【答案】     ‎ ‎10.  ．‎ ‎【答案】     ‎ ‎11. 有一列正方体，棱长组成以 为首项， 为公比的等比数列，体积分别记为 ，则  ．‎ ‎【答案】     ‎ ‎12. 若函数 在 处连续，则  ，  ．‎ ‎【答案】     ； ‎ ‎13. =  ．‎ ‎【答案】     ‎ ‎14. 设函数 ，点 表示坐标原点，点 ，若向量 ， 是 与 的夹角，（其中 ），设 ，则  ．‎ ‎【答案】     ‎ ‎【分析】     ．由题意，得 是 与 轴正方向 的夹角，从而 ．运用裂项相消法，得 ．‎ ‎15. 设等差数列 的前 项和为 ，若 ，则  ‎ ‎【答案】     ‎ ‎【分析】     故 ，所以 ，．‎ ‎16.  ．‎ ‎【答案】     ‎ ‎17. 计算  ．‎ ‎【答案】     ‎ ‎18. (1)若 ，则常数  ．‎ ‎(2)  ．‎ ‎【答案】     ； ‎ ‎19. 已知无穷等比数列 的各项和为 ，则首项 的取值范围是  ．‎ ‎【答案】     ‎ ‎20. 已知函数 在 处连续，则实数 的值为  ．‎ ‎【答案】     ‎ ‎21. 设函数 在 处连续，求 的值．‎ ‎【解】        ‎ 而 ，所以 ‎ ‎ ‎ ‎22. 已知 ，求 的值．‎ ‎【解】        解法一：∵ ，‎ ‎    ∴ 为方程 的根．‎ ‎    ∴ ．‎ ‎    又 ，‎ ‎    ∴ ．‎ ‎    ∴ ．‎ ‎     ‎ ‎    解法二： ‎ ‎ ∴ ．‎ ‎    同上可得 ．‎ ‎23. 在数列 中，若 ， 是正整数，且 ， 则称 为“绝对差数列”．‎ ‎    (1)举出一个前五项不为零的"绝对差数列"（只要求写出前十项）；‎ ‎【解】         ，，，，，，，，，．（答案不唯一）‎ ‎    (2)若“绝对差数列” 中，，，试求出通项 ；‎ ‎【解】        因为在绝对差数列 中，，，‎ ‎    所以该数列是 ，，，，，，，，．‎ ‎    即自第 项开始，每三个相邻的项周期地取值 ，，，‎ ‎    所以 ‎ ‎    (3)证明：任何“绝对差数列”中总含有无穷多个为零的项．‎ ‎【解】        根据定义，数列 必在有限项后出现零项，证明如下：‎ ‎    假设 中没有零项，由于 ，所以对于任意的 ，都有 ，从而 ‎    当 时，；‎ ‎    当 时，；‎ ‎    即 的值要么比 至少小 ，要么比 至少小 ．‎ ‎    令 ．‎ ‎    则 ．‎ ‎    由于 是确定的正整数，这样减少下去，必然存在某项 ，‎ ‎    这与 矛盾，从而 必有零项．‎ ‎    若第一次出现的零项为第 项，记 ，则自第 项开始，每三个相邻的项周期地取值 ，，，即 ‎     ‎ ‎    所以绝对差数列 中有无穷多个为零的项．‎ ‎24. 已知数列 的通项公式为 ，求 的值．‎ ‎【解】        因为 ‎ ‎ 所以 ‎ ‎ ‎ ‎25. 已知数列 中， 为其前 项的和，求 的值．‎ ‎【解】         ‎ ‎     ‎ ‎     ‎ ‎26. 已知数列 ，其中 ，， ．记数列 的前 项和为 ，数列 的前 项和为 ．‎ ‎    (1)求 ；‎ ‎【解】        由题意，得 是首项为 、公差为 的等差数列，则其前 项和 从而 因此 ‎    (2)设 ，，（其中 为 的导函数），计算 ．‎ ‎【解】        由（1），得 则 从而 ‎ ‎ 因此 ‎ ‎ ‎ ‎27. 已知等差数列 的前三项为 ，，，前 项和为 ，且 ．‎ ‎    (1)求 及 的值；‎ ‎【解】         ‎ ‎     数列 是首项为 ，公差为 的等差数列．‎ ‎     ‎ ‎    即 、 的值分别为 、 ．‎ ‎    (2)求 的值．‎ ‎【解】         ‎ ‎     ‎ ‎     ‎ ‎     ‎ ‎28. 已知数列 的前 项和 ，数列 满足 ，，记数列 的前 项和为 ．‎ ‎    (1)证明： 为等比数列；‎ ‎【解】        因为数列 的前 项和 ，‎ ‎    所以 ．‎ ‎    因为 时，，也适合上式，‎ ‎    所以 ．‎ ‎    因为 ，‎ ‎    所以数列 是首项为 ，公比为 的等比数列．‎ ‎    (2)求 ；‎ ‎【解】        当 时，，将其变形为 ，即 ．‎ ‎    所以数列 是首项为 ，公差为 的等差数列．‎ ‎    所以 ．‎ ‎    所以 ．‎ ‎    因为 ，‎ ‎    所以 ．‎ ‎    两式相减得 ．‎ ‎    整理得 ．‎ ‎    (3)设 ，若对于任意 ，都有 成立，求实数 的取值范围．‎ ‎【解】        由 ，得 ．‎ ‎    于是 化为 ‎ ‎    （i）当 是正奇数时， 式可化为 ，显然， 大于 ，且随着正奇数 的增大而减小．‎ ‎    由于 式对任意正奇数 恒成立，‎ ‎    所以 ．‎ ‎    （ii）当 是正偶数时， 式可化为 ，显然， 随着正偶数 的增大而减小．‎ ‎    由于 式对任意正偶数 恒成立，‎ ‎    所以 ．‎ ‎    综上，实数 的取值范围 ．‎ ‎29. 设函数 ，其中 ，已知对一切 ，有 和 ，求证：．‎ ‎【解】        由于 则 所以 由于 ‎ ‎ 故有 ．‎ ‎30. 已知公比为 的无穷等比数列 各项的和为 ，无穷等比数列 各项的和为 ．‎ ‎    (1)求数列 的首项 和公比 ；‎ ‎【解】        依题意可知，‎ ‎ ‎ ‎    (2)对给定的 ，设 是首项为 ，公差为 的等差数列，求 的前 项之和；‎ ‎【解】        由（1）知，，所以数列 的的首项为 ，公差 ，‎ ‎     ，即数列 的前 项之和为 ．‎ ‎    (3)设 为数列 的第 项，，求 ，并求正整数 ，使得 存在且不等于零．‎ ‎    （注：无穷等比数列各项的和即当 时该无穷等比数列前 项和的极限）‎ ‎【解】        ‎ 所以 令 因为 所以 故 当 时，‎ 当 时，，所以当 时， 存在且不等于零．‎ ‎31. 已知在 轴上有一点列：，，，，，，点 分有向线段 所成的比为 ，其中 ， 为常数，，．‎ ‎    (1)设 ，求数列 的通项公式；‎ ‎【解】        由题意得 ，又 ，‎ ‎     ，‎ ‎    又 ，‎ ‎     数列 是首项为 、公比为 的等比数列，‎ ‎     ．‎ ‎    (2)设 ，当 变化时，求 的取值范围．‎ ‎【解】         因为 ‎ ．‎ ‎     ，．‎ ‎     当 时，．‎ ‎32. 已知函数 数列 满足 ．‎ ‎    (1)求数列 的通项公式；‎ ‎【解】         ，所以 所以 所以 ‎ ‎ 将这 个式子相加，得 ‎ ，‎ ‎     ，所以 ‎    (2)设 轴，直线 与函数 的图象所围成的封闭图形的面积为 ，求 ；‎ ‎【解】         为一直角梯形（ 时为直角三角形）的面积，该梯形的两底边的长分别为 ，，高为 ，所以 ‎ ‎ ‎ ‎    (3)在集合 中，是否存在正整数 ，使得不等式 对一切 恒成立？若存在，则这样的正整数 共有多少个？并求出满足条件的最小的正整数 ；若不存在，请说明理由．‎ ‎【解】        设满足条件的正整数 存在，则 又 ，‎ ‎     均满足条件．‎ ‎    它们构成首项为 ，公差为 的等差数列．‎ ‎    设共有 个满足条件的正整数 ，则 解得 ‎ 中满足条件的正整数 存在，共有 个，所以 ‎    (4)请构造一个与 有关的数列 ，使得 存在，并求出这个极限值．‎ ‎【解】        设 ，即 则 显然，其极限存在，并且 注：（c为非零常数）， 等都能使 存在．‎ ‎33. 已知 ，且 ，函数 ．‎ ‎    (1)求函数 的定义域，并判断 的单调性；‎ ‎【解】        由题意知 ，当 时， 的定义域是 ‎ ‎ 当 时， 的定义域是 ‎ 因为 ‎ 由此，‎ ‎    当 时， ，因为 ， ，则 ‎ 所以 在 上是减函数．‎ ‎    当 时， ，因为 ， ，则 ‎ 所以 在 上是减函数．‎ ‎    (2)若 ，求 ；‎ ‎【解】        因为 ‎ ‎ 所以 ‎ ‎ 由函数定义域知 ，因为 是正整数，则 ，所以 ‎ ‎    (3)当 （ 为自然对数的底数）时，设 ，若函数 的极值存在，求实数 的取值范围以及函数 的极值．‎ ‎【解】        由 ，所以 ‎ ‎ 令 ，即 ‎ ‎ 由题意应有 ，即 ‎ ‎ ①当 时， 有实根 ‎ 在 点左右两侧均有 ，故 无极值．‎ ‎    ②当 时， 有两个实根 ‎ ‎ 当 变化时， 、 的变化情况如下表所示： ‎ ‎ 所以 的极大值为 ‎ ‎ 的极小值为 ‎ ‎ ③当 时, 在定义域内有一个实根 ‎ ‎ 同上可得 的极大值为 ‎ 综上所述，‎ ‎    当 时 的极大值为 ， 的极小值为 ；‎ ‎    当 时， 的极大值为 ．‎ ‎34. 已知 是直角坐标系平面 到自身的一个映射，点 在映射 下的象为点 ，记作 ．设 ，，，，， 如果存在一个圆，使所有的点 都在这个圆内或圆上，那么称这个圆为点 的一个收敛圆．特别地，当 时，则称点 为映射 下的不动点．若点 在映射 下的象为点 ．‎ ‎    (1)求映射 下不动点的坐标；‎ ‎【解】        设不动点的坐标为 ，由题意，得 解得 所以此映射 下不动点为 ．‎ ‎    (2)若 的坐标为 ，求证：点 存在一个半径为 的收敛圆．‎ ‎【解】        由 ，得 所以 因为 ，，所以 ，，所以 由等比数列定义，得数列 是公比为 ，首项为 的等比数列，所以 则 同理，．‎ ‎    所以 ．‎ ‎    设 ，则 因为 ，所以 ，所以 故所有的点 都在以 为圆心， 为半径的圆内，即点 存在一个半径为 的收敛圆．‎ ‎35. 设 是定义在 上的偶函数，其图象关于直线 对称，对任意 ，都有 ，且 ．‎ ‎    (1)求 ；‎ ‎【解】        因为对任意 ，都有 ，‎ ‎    所以 ．‎ ‎     ‎ ‎     ， ．‎ ‎    (2)证明 是周期函数；‎ ‎【解】        依题设 关于直线 对称，故 ，即 又由 是偶函数知 ， ．‎ ‎    将上式中 以 代换，得 这表明 是 上的周期函数，且 是它的一个周期．‎ ‎    (3)记 ，求 ．‎ ‎【解】        由（1）知 ，‎ ‎     ‎ ‎ ，‎ ‎     ． 的一个周期是 ‎ ‎     ，因此 ．‎ ‎     ．‎ ‎36. 已知点 ，，…，（ 为正整数）都在函数 的图象上，其中 是以 为首项， 为公差的等差数列．‎ ‎    (1)求数列 的通项公式，并证明数列 是等比数列；‎ ‎【解】         ，，， （定值）， 数列 是等比数列．‎ ‎    (2)设数列 的前 项的和为 ，求 ；‎ ‎【解】         是等比数列，且公比 ， ，．‎ ‎    当 时，；‎ ‎    当 时，．‎ ‎    因此，．‎ ‎    (3)设 ，当 时，问 的面积是否存在最大值？若存在，求出最大值；若不存在，请说明理由；‎ ‎【解】         ，，设 ，当 最大时，则 ，解得 ，， 时， 取得最大值 ，因此 的面积存在最大值为 ．‎ ‎37. 如图，已知 中，，，，在 内有一系列正方形，求所有这些正方形面积之和．‎ ‎【解】        设正方形 、 、 的边长分别为 ，‎ ‎     ，，．‎ ‎    由相似三角形的知识可得 ，．‎ ‎    同理，可得 ‎ ‎     是以 为首项，以 为公比的等比数列．‎ ‎    设 是第 个正方形的面积，则 是以 为首项， 为公比的等比数列．‎ ‎     ‎ ‎    即所有这些正方形面积之和为 ．‎ ‎38. 已知数列 是等差数列，公差为 ，，．‎ ‎    (1)用 表示 ；‎ ‎【解】        因为数列 是公差为 的等差数列，所以 去分母，得 由 ，得 ‎    (2)若 ，且 ，求 的值；‎ ‎【解】        ‎ 当 时，‎ 这与已知矛盾，所以 ，‎ ‎    当 时，‎ 综上，．‎ ‎    (3)在（2）的条件下，求数列 的前 项和．‎ ‎【解】        当 ，由已知，得 解得 令 则 两式相减，得 从而 而 因此，数列 的前 项和 ‎39. 讨论函数 在 处的左极限、右极限以及在 处的极限．‎ ‎【解】        函数 的图象如图所示：‎ ‎    ‎ ‎    当 时，函数无限接近于 即 ‎ ‎    当 时，函数无限接近于 即 ‎ ‎    综上，可知 ．‎ ‎     函数 在 处极限不存在．‎ ‎40. 已知 ，数列 满足 ，，．‎ ‎    (1)已知数列 极限存在且大于零，求 （将 用 表示）；‎ ‎【解】        由 存在，且 对 两边取极限得 解得 又 ，所以 ‎    (2)设 ，，证明：；‎ ‎【解】        由 ，，得 所以 即 对 都成立．‎ ‎    (3)若 对 都成立，求 的取值范围．‎ ‎【解】        令 ，根据（1）（2）得 解得 现证明当 时， 对 都成立．‎ ‎    （i）当 时结论成立（已验证）．‎ ‎    （ii）假设当 时结论成立，即 那么 则只须证明 即证 对 成立．由于 而当 时，‎ 所以 从而 即 故当 时，‎ 即 时结论成立．‎ ‎    根据（i）和（ii）可知结论对一切正整数都成立．‎ ‎    故 对 都成立的 的取值范围为 ‎ 课后练习 ‎ 1. 无限循环小数可以化为有理数，如 ，，，，请你归纳出  （表示成最简分数 ，且 ，）．‎ ‎ 2. 计算：  ．‎ ‎ 3. 已知 ，则  ，  ．‎ ‎ 4. 已知函数 是连续函数，则实数 的值是  ．‎ ‎ 5. 计算：  ．‎ ‎ 6. 若 ，则  ．‎ ‎ 7.  ．‎ ‎ 8.  ．‎ ‎ 9. 计算：  ．‎ ‎10. 若 展开式的第三项为 ，则  ．‎ ‎11. 已知函数 是连续函数，则实数 的值是  ．‎ ‎12. 等差数列 的前 项的和为 ，前 项的和为 ，则其首项为  ，若数列 的前 项的和为 ，则  ．‎ ‎13. 已知 在定义域 上可导，导函数为 ，若 ，，则  ．（用 ， 表示）．‎ ‎14. 已知定义在正实数集上的连续函数 ，则实数 的值为  ．‎ ‎15.  ．‎ ‎16.  ．‎ ‎17. (limlimits limits_{x o 1} left(dfrac{1}{{x - 1}} - dfrac{2}{{{x^2} - 1}} ight)=)  ．‎ ‎18.  ．‎ ‎19. 等比数列 ，其前 项和为 ，则  ．‎ ‎20. 计算  ．‎ ‎21. 已知数列 的前 项和 ．‎ ‎    (1)求 ；‎ ‎    (2)证明：．‎ ‎22. 函数 定义在 上，满足 且 ，在每个区间 上， 的图象都是平行于 轴的直线的一部分．‎ ‎    (1)求 及 的值，并归纳出 的表达式；‎ ‎    (2)设直线 轴及 的图象围成的矩形的面积为 ，求 ， 及 的值．‎ ‎23. 已知定义在 上的函数 和数列 满足下列条件：‎ ‎ ，‎ ‎ ‎ 其中 为常数， 为非零常数．‎ ‎    (1)令 ，证明数列 是等比数列；‎ ‎    (2)求数列 的通项公式；‎ ‎    (3)当 时，求 ‎ ‎24. 已知 ．‎ ‎    (1)当 时，求数列 的前 项和 ；‎ ‎    (2)求 ．‎ 数列极限与函数极限-出门考 姓名                                                                 成绩                                  ‎ ‎ 1. 若 ，则常数  ．‎ ‎ 2. 的值等于  ．‎ ‎ 3. 设等差数列 的公差 是 ，前 项的和为 ，则  ．‎ ‎ 4. 的值等于  ．‎ ‎ 5. 极限  ．‎ ‎ 6. 各项均为正数的等比数列 的公比为 ，前 项和为 ．若 ，则  ，若 ，则  ．‎ ‎ 7. 设常数 ， 展开式中 的系数为 ，则  ，  ．‎ ‎ 8. 设 是 展开式中 的系数，则 =  ．‎ ‎ 9.  ．‎ ‎10. 设函数 在 处连续，则实数 的值为  ．‎ ‎11. 若 ，则  ，  ．‎ ‎12.  ．‎ ‎13. 等比数列 ，，，， 所有项的和为  ．‎ ‎14. 若 ，则实数  ．‎ ‎15. 已知函数 ，若 在 上连续，则  ．此时  ．‎ ‎16. 已知点 ， 和点 ，记 的中点为 ，取 和 中的一条，记其端点为 ，，使之满足 ，记 的中点为 ，取 和 中的一条，记其端点为 ，，使之满足 ．依次下去，得到 ，，，，，则  ．‎ ‎17. 在二项式 的展开式中，含 项的系数记为 ，则 的值为  ．‎ ‎18. 若 的展开式中各项系数的和是 ， 的二项式系数和为 ，则  ．‎ ‎19. 已知数列 的前 项和 ，则  ．‎ ‎20. 已知点 ，其中 为正整数．设 表示 外接圆的面积，则  ．‎