黑龙江省大庆中学2019-2020学年高一下学期期中考试数学试题

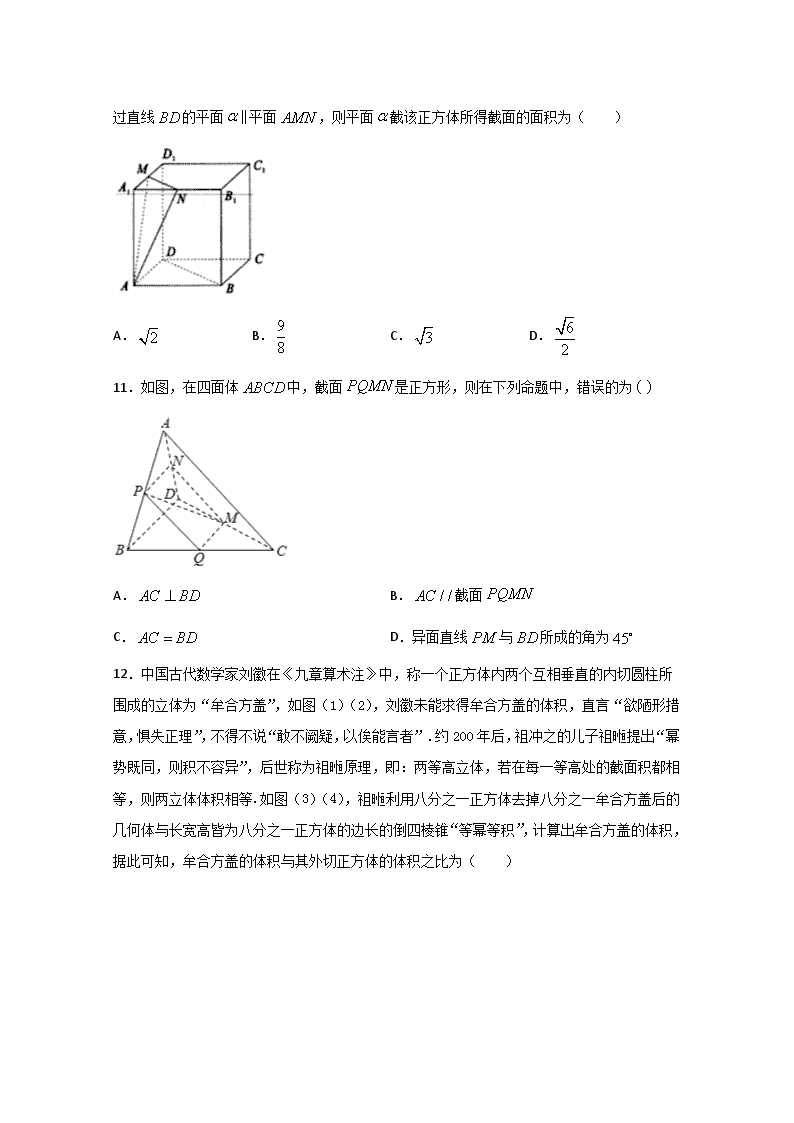
黑龙江省大庆中学2019-2020学年高一下学期期中考试数学试题

大庆中学2019---2020学年度下学期阶段性检测 高一年级数学试题 ‎ ‎ 一、选择题（本大题共12个小题，每题5分，共60分）‎ ‎1．不等式的解集为（ ）‎ A． B．或 C．或 D．‎ ‎2．一个几何体的三视图如图所示，则该几何体的体积为（ ）‎ A． B． C． D．‎ ‎3．设.若是与的等比中项，则的最小值（ ）‎ A． B． C． D．‎ ‎4．已知x，y满足约束条件，则的最小值是（ ）‎ A．8 B．‎6 ‎C．3 D．3‎ ‎5．空间中，是三个互不重合的平面，是一条直线，则下列命题中正确的是（ ）‎ A．若，，则 B．若，，则 C．若，，则 D．若，，则 ‎6．把按斜二测画法得到（如图所示），其中，，那么是一个（ ）‎ A．等边三角形 B．直角三角形 C．等腰三角形 D．三边互不相等的三角形 ‎7．在正方体中，E为棱的中点，则异面直线AE与所成角的余弦值为（ ）‎ A． B． C． D．‎ ‎8．如图，在直三棱柱中，为等边三角形，，，则三棱柱的外接球的表面积为（ ）‎ A． B．‎ C． D．‎ ‎9．一竖立在水平面上的圆锥物体的母线长为‎2m，一只蚂蚁从圆锥的底面圆周上的点P出发，绕圆锥表面爬行一周后回到P点，蚂蚁爬行的最短路径为，则圆锥的底面圆半径为（ ）‎ A．‎1m B． C． D．‎ ‎10．如图，在棱长为1的正方体中，，分别是，‎ 的中点，过直线的平面平面，则平面截该正方体所得截面的面积为（ ）‎ A． B． C． D．‎ ‎11．如图，在四面体中，截面是正方形，则在下列命题中，错误的为 A． B．截面 C． D．异面直线与所成的角为 ‎12．中国古代数学家刘徽在《九章算术注》中，称一个正方体内两个互相垂直的内切圆柱所围成的立体为“牟合方盖”，如图（1）（2），刘徽未能求得牟合方盖的体积，直言“欲陋形措意，惧失正理”，不得不说“敢不阙疑，以俟能言者”.约200年后，祖冲之的儿子祖暅提出“幂势既同，则积不容异”，后世称为祖暅原理，即：两等高立体，若在每一等高处的截面积都相等，则两立体体积相等.如图（3）（4），祖暅利用八分之一正方体去掉八分之一牟合方盖后的几何体与长宽高皆为八分之一正方体的边长的倒四棱锥“等幂等积”，计算出牟合方盖的体积，据此可知，牟合方盖的体积与其外切正方体的体积之比为（ ）‎ A． B． C． D．‎ 二、解答题（本大题共2个小题，每题20分，共40分)‎ ‎13．已知数列为等差数列，公差，且，.‎ ‎（1）求数列的通项公式；‎ ‎（2）令，求数列的前项和.‎ ‎14．如图，已知四棱锥中，底面为平行四边形，点，，分别是，，的中点．‎ ‎（1）求证：平面；‎ ‎（2）求证：平面平面．‎ 大庆中学2019---2020学年度阶段性检测 高一年级数学答案 ‎ ‎2020年6月8日 星期一 一、选择题（本大题共12个小题，每题5分，共60分）‎ ‎1． ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 直接解出即可.‎ ‎【详解】‎ 由可得，所以或 故选：B ‎【点睛】‎ 本题考查的是一元二次不等式的解法，较简单.‎ ‎2． ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 由三视图可得该几何体为圆柱的一半,进而求解即可.‎ ‎【详解】‎ 由图,该几何体为圆柱的一半,‎ 则,‎ 故选:B ‎【点睛】‎ 本题考查由三视图还原几何体,考查圆柱的体积.‎ ‎3． ‎ ‎【答案】C ‎【解析】‎ 由题意可得：，则：‎ ‎，‎ 当且仅当时等号成立，‎ 综上可得：的最小值是4.‎ 本题选择C选项.‎ 点睛：在应用基本不等式求最值时，要把握不等式成立的三个条件，就是“一正——各项均为正；二定——积或和为定值；三相等——等号能否取得”，若忽略了某个条件，就会出现错误．‎ ‎4．‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 根据约束条件画出可行域，然后将目标函数化为斜截式，得到过点时，直线的截距最小，从而得到答案.‎ ‎【详解】‎ 画出不等式组表示的平面区域，如图中阴影部分所示，‎ 易求得， ‎ ‎，则，‎ 当直线过点时，z取到最小值，‎ 所以的最小值是，‎ 故选：B．‎ ‎【点睛】‎ 本题考查线性规划求最值，属于简单题.‎ ‎5． ‎ ‎【答案】C ‎【解析】‎ 若l∥α，l∥β，则α与β可能平行也可能相交(此时交线与l平行)，故A错误；‎ 若，，则l∥α或l⊂α，故B错误；‎ 若，，则l与β可能平行也可能相交，故D错误；‎ 若l∥β，则存在直线m⊂β，使得l∥m，又由l⊥α可得m⊥α，故α⊥β，故C正确；‎ 本题选择C选项.‎ ‎6．‎ A．等边三角形 B．直角三角形 C．等腰三角形 D．三边互不相等的三角形 ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据斜二侧画法还原在直角坐标系的图形，进而分析出△ABC的形状．‎ ‎【详解】‎ 根据斜二侧画法还原在直角坐标系的图形，如下图所示：‎ 由图易得，故为等边三角形，故选A．‎ ‎【点睛】‎ 本题考查的知识点是斜二侧画法，三角形形状的判断，解答的关键是斜二侧画法还原在直角坐标系的图形．‎ ‎7． ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 连接，易知等于异面直线与所成的角，设正方体的棱长为2，利用余弦定理，即可得答案；‎ ‎【详解】‎ 连接，易知为异面直线与所成的角.‎ 设正方体的棱长为2，‎ 在中，，‎ 由余弦定理可知，‎ 所以异面直线与所成角的余弦值为．‎ 故选：C.‎ ‎【点睛】‎ 本题考查异面直线AE与所成角，考查空间想象能力、运算求解能力，求解时注意余弦定理的应有.‎ ‎8． ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 直三棱柱中，上下底面平行且全等，可得直三棱柱外接球的球心为上下底面外接圆圆心连线的中点，求出底面外接圆半径，即可求解.‎ ‎【详解】‎ 如下图所示，取，的外接圆的圆心分别为，‎ 连接，取的中点，‎ 则是三棱柱的外接球的球心，‎ 设的外接圆的半径为，‎ 三棱柱的外接球的半径为，‎ 由正弦定理得，∵，‎ ‎∴，即，又，‎ 所以，所以，‎ 所以外接球的表面积为.‎ 故选：B.‎ ‎【点睛】‎ 本题考查多面体与球的“外接”“内切”问题，确定球心位置是解题关键，属于中档题.‎ ‎9． ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 将圆锥展开后的扇形画出，结合母线及最短距离，即可确定圆心角大小；进而求得弧长，即为底面圆的周长，由周长公式即可求得底面圆的半径.‎ ‎【详解】‎ 将圆锥侧面展开得半径为‎2m的一扇形，蚂蚁从爬行一周后回到（记作），作，如下图所示：‎ 由最短路径为，即，‎ 由圆的性质可得，即扇形所对的圆心角为，‎ 则圆锥底面圆的周长为，‎ 则底面圆的半径为，‎ 故选：B.‎ ‎【点睛】‎ 本题考查了了圆锥侧面展开图、扇形弧长公式的简单应用，属于基础题.‎ ‎10． ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 取的中点为，可证得平面平面，即的面积即为所求，然后利用梯形的面积公式求解即可.‎ ‎【详解】‎ 取的中点为.‎ 易知，，所以四边形为平行四边形，所以.‎ 又和为平面的两条相交直线，所以平面平面，即的面积即为所求.‎ 由，，所以四边形为梯形，高为.‎ 所以面积为：.‎ 故选B.‎ ‎【点睛】‎ 本题主要考查的知识点是空间立体几何中截面的形状的判断，面面平行性质，四棱柱的结构特征，解答本题的关键是画出截面，并分析其几何特征，属于中档题.‎ ‎11． ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 首先由正方形中的线线平行推导线面平行，再利用线面平行推导线线平行，将AC、BD平移到正方形内，即可利用平面图形知识作出判断．‎ ‎【详解】‎ 因为截面PQMN是正方形，所以PQ∥MN、QM∥PN，‎ 则PQ∥平面ACD、QM∥平面BDA，‎ 所以PQ∥AC，QM∥BD，‎ 由PQ⊥QM可得AC⊥BD，故A正确；‎ 由PQ∥AC可得AC∥截面PQMN，故B正确；‎ 异面直线PM与BD所成的角等于PM与QM所成的角，故D正确；‎ 综上C是错误的．‎ 故选C．‎ ‎【点睛】‎ 本题主要考查线面平行的性质与判定，考查了异面直线所成角的定义及求法，属于基础题．‎ ‎12． ‎ ‎【答案】B ‎【解析】‎ 设正方体的边长为，因为，，所以 ‎，故选B．‎ 二、解答题（本大题共2个小题，每题20分，共40分)‎ ‎13．‎ ‎【答案】（1）；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）利用题目所给两个已知条件求出首项和公差，由此求得数列的通项公式.（2）由（1）求得的表达式，再利用裂项求和法求得数列的前项和.‎ ‎【详解】‎ ‎（1）由题意可知，，.‎ 又， ，，，，‎ ‎.故数列的通项公式为.‎ ‎（2）由（1）可知， ，‎ ‎.‎ ‎【点睛】‎ 本小题主要考查等差数列通项公式的求解，考查裂项求和法求数列的前项和.求等差数列通项公式的题目，往往会给两个条件，将两个条件解方程组，可求得，由此可求得等差数列的通项公式.如果数列是两个等差数列乘积的倒数的形式，那么可以利用裂项求和法求得前项和.‎ ‎14．‎ ‎【答案】（1）见解析（2）见解析 ‎【解析】‎ ‎【试题分析】（1）根据三角形的中位线，可得，由此证得平面.（2）利用中位线证明,，故，由（1）得，由此可得平面平面.‎ ‎【试题解析】‎ ‎（1）由题意：四棱锥的底面为平行四边形，点，，分别是，，的中点，‎ ‎∴是的中点，‎ ‎∴，‎ 又∵平面，平面，‎ ‎∴平面．‎ ‎（2）由（1），知，‎ ‎∵，分别是，的中点，‎ ‎∴，‎ 又∵平面，平面，，平面，平面，，‎ ‎∴平面平面． ‎ ‎【点睛】本题主要考查线面平行的判定定理，考查面面平行的判定定理.要证明线面平行，需在平面内找到一条直线和要证的直线平行，一般寻找的方法有三种：一是利用三角形的中位线，二是利用平行四边形，三是利用面面平行.要证面面平行，则需证两条相交直线和另一个平面平行.‎