2018届二轮复习圆锥曲线的方程课件（全国通用）(1)

2018届二轮复习圆锥曲线的方程课件（全国通用）(1)

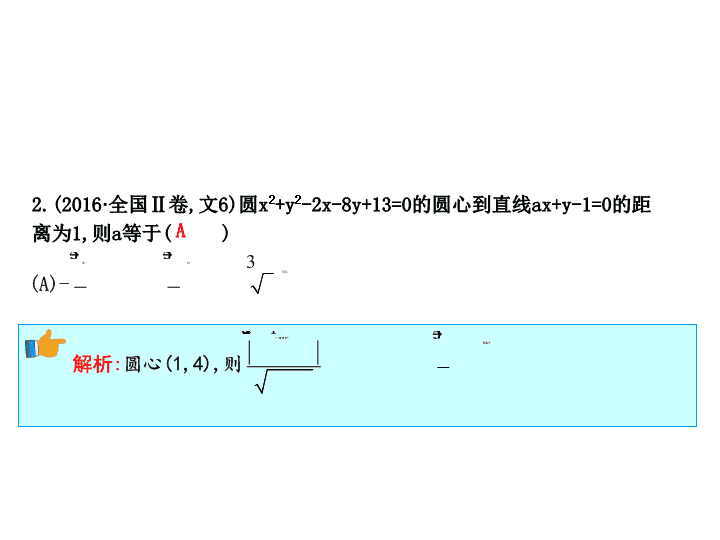
圆锥曲线的方程 B 2 .(2016 · 全国 Ⅱ 卷 , 文 6) 圆 x 2 +y 2 -2x-8y+13=0 的圆心到直线 ax+y-1=0 的距离为 1, 则 a 等于 ( 　 　 ) A B D 解析 : 由题知 P(1,2),k=2. 故选 D. D 【 教师备用 】 (2014 · 全国 Ⅰ 卷 , 文 10) 已知抛物线 C:y 2 =x 的焦点为 F,A(x 0 ,y 0 ) 是 C 上一点 ,|AF|= x 0 , 则 x 0 等于 ( 　 　 ) (A)1 (B)2 (C)4 (D)8 A 6. (2015 · 全国 Ⅰ 卷 , 文 20) 已知过点 A(0,1) 且斜率为 k 的直线 l 与圆 C:(x-2) 2 +(y-3) 2 =1 交于 M,N 两点 . (1) 求 k 的取值范围 ; 高考感悟 1. 考查角度 高考对直线与圆这部分内容主要考查圆的方程及应用、直线与圆的位置关系 , 而对直线的倾斜角和斜率、直线的方程、两直线的平行与垂直、点到直线的距离等一般很少单独考查 , 高考对圆锥曲线主要考查椭圆、双曲线、抛物线的定义、方程与性质 . 2. 题型及难易度 选择、填空题 . 难度为中档 . 热点突破 剖典例 · 促迁移 直线、圆的方程及应用 热点一 答案 : (x-2) 2 +y 2 =9 【 方法技巧 】 (1) 在求解直线相关问题时 , 要注意其方程的形式 , 如在应用点到直线的距离公式 d= 时 , 一定要将直线方程化成一般形式 , 正确写出 A,B,C 的值 , 此处符号易出现错误 . (2) 求圆的方程一般有两类方法 :① 几何法 , 通过研究圆的性质、直线和圆、圆与圆的位置关系 , 进而求得圆的基本量 ;② 代数法 , 即用待定系数法先设出圆的方程 , 再由条件列出方程组求得各系数 . 热点训练 1:(1) (2014 · 福建卷 , 文 6) 已知直线 l 过圆 x 2 +(y-3) 2 =4 的圆心 , 且与直线 x+y+1=0 垂直 , 则 l 的方程是 ( 　　 ) (A)x+y-2=0 (B)x-y+2=0 (C)x+y-3=0 (D)x-y+3=0 解析 : (1) 依题意 , 得直线 l 过点 (0,3), 斜率为 1, 所以直线 l 的方程为 y-3=x-0, 即 x-y+3=0. 故选 D. (2) (2015 · 北京卷 , 文 2) 圆心为 (1,1) 且过原点的圆的方程是 ( 　　 ) (A)(x-1) 2 +(y-1) 2 =1 (B)(x+1) 2 +(y+1) 2 =1 (C)(x+1) 2 +(y+1) 2 =2 (D)(x-1) 2 +(y-1) 2 =2 直线、圆的位置关系 热点二 考向 1 　直线和圆的位置关系 【 例 2】 (2016 · 全国 Ⅰ 卷 , 文 15) 设直线 y=x+2a 与圆 C:x 2 +y 2 -2ay-2=0 相交于 A,B 两点 , 若 |AB|=2 , 则圆 C 的面积为 　　　　 .   答案 : 4π 考向 2 　圆与圆的位置关系 【 例 3】 (2016 · 山东卷 , 文 7) 已知圆 M:x 2 +y 2 -2ay=0(a>0) 截直线 x+y=0 所得线段的长度是 2 . 则圆 M 与圆 N:(x-1) 2 +(y-1) 2 =1 的位置关系是 ( 　　 ) (A) 内切 (B) 相交 (C) 外切 (D) 相离 【 方法技巧 】 研究直线与圆的位置关系主要通过圆心到直线的距离和半径的比较实现 , 两个圆的位置关系的判断依据是两圆心距离与两半径差与和的比较 . 热点训练 2: (2015 · 安徽卷 , 文 8) 直线 3x+4y=b 与圆 x 2 +y 2 -2x-2y+1=0 相切 , 则 b 的值是 ( 　　 ) (A)-2 或 12 (B)2 或 -12 (C)-2 或 -12 (D)2 或 12 圆锥曲线的定义与标准方程 热点三 考向 1 　圆锥曲线的定义及应用 【 方法诠释 】 在圆锥曲线中求最值问题通常根据圆锥曲线定义及平面几何中两点之间线段最短的原理 , 把要求式转化为某个最值使问题解决 . 考向 2 　圆锥曲线的方程 【 方法技巧 】 (1) 对于圆锥曲线的定义不仅要熟记 , 还要深入理解细节部分 , 比如椭圆的定义中要求 |PF 1 |+|PF 2 |>|F 1 F 2 |, 双曲线的定义中要求 ||PF 1 |-|PF 2 ||<|F 1 F 2 |, 抛物线上的点到焦点的距离与到准线的距离相等的转化 . (2) 重视定义在解题中的应用 , 灵活地进行抛物线上的点到焦点的距离与到准线距离的等价转化 , 是解决抛物线焦点弦有关问题的重要途径 . 圆锥曲线的几何性质 热点四 答案 : (1)A 答案 : (2)2 【 方法技巧 】 解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于 a,b,c 的方程 ( 组 ) 或不等式 ( 组 ), 再根据 a,b,c 的关系消掉 b 得到 a,c 的关系式 . 建立关于 a,b,c 的方程 ( 组 ) 或不等式 ( 组 ), 要充分利用椭圆和双曲线的几何性质、点的坐标的范围等 .