- 2021-06-24 发布 |
- 37.5 KB |
- 2页

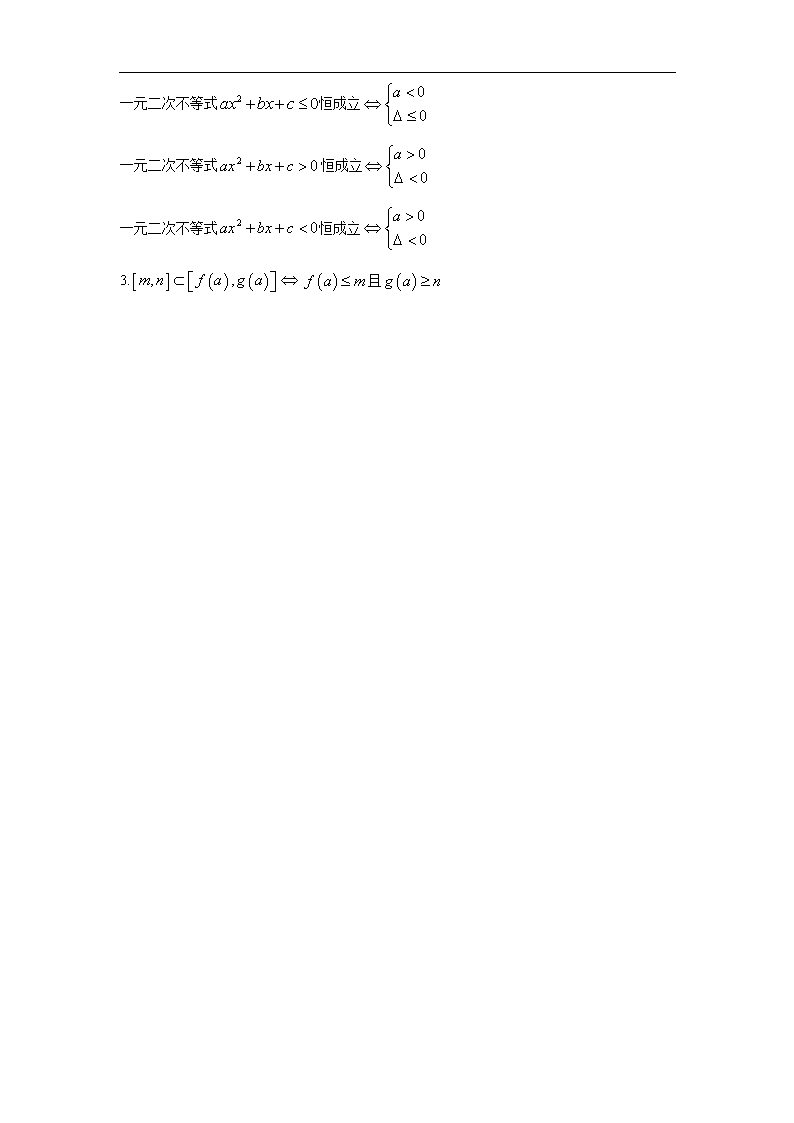
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学专题复习教案: 恒成立问题
不等式恒成立问题 主标题:不等式恒成立问题 副标题:为学生详细的分析不等式恒成立的高考考点、命题方向以及规律总结。 关键词:不等式,不等式恒成立,知识总结 难度:3 重要程度:5 考点剖析:会已知一个变量的取值范围,求另一个变量的取值范围. 命题方向: “含参不等式恒成立问题”把不等式、函数、三角、几何等内容有机地结合起来,其以覆盖知识点多,综合性强,解法灵活等特点而倍受高考命题者的青睐。另一方面,在解决这类问题的过程中涉及的“函数与方程”、“化归与转化”、“数形结合”、“分类讨论”等数学思想对锻炼学生的综合解题能力,培养其思维的灵活性、创造性都有着独到的作用。 规律总结: 解决不等式恒成立问题常见的方法: 一、 分离参数 在给出的不等式中,如果能通过恒等变形分离出参数,即:若恒成立,只须求出,则;若恒成立,只须求出,则,转化为函数求最值。 二、 分类讨论 在给出的不等式中,如果两变量不能通过恒等变形分别置于不等式的两边,则可利用分类讨论的思想来解决。 三、 确定主元 在给出的含有两个变量的不等式中,学生习惯把变量看成是主元(未知数),而把另一个变量看成参数,在有些问题中这样的解题过程繁琐。如果把已知取值范围的变量作为主元,把要求取值范围的变量看作参数,则可简化解题过程。 四、 利用集合与集合间的关系 在给出的不等式中,若能解出已知取值范围的变量,就可利用集合与集合之间的包含关系来求解,即:,则且,不等式的解即为实数的取值范围。 五、 数形结合 数形结合法是先将不等式两端的式子分别看作两个函数,且正确作出两个函数的图象,然后通过观察两图象(特别是交点时)的位置关系,列出关于参数的不等式。 知识点总结: 1. 恒成立 恒成立 2. 一元二次不等式恒成立 一元二次不等式恒成立 一元二次不等式恒成立 一元二次不等式恒成立 3.且查看更多