第08章 检测B卷（理）-2020年领军高考数学一轮复习（文理通用） Word版含解析

第08章 检测B卷（理）-2020年领军高考数学一轮复习（文理通用） Word版含解析

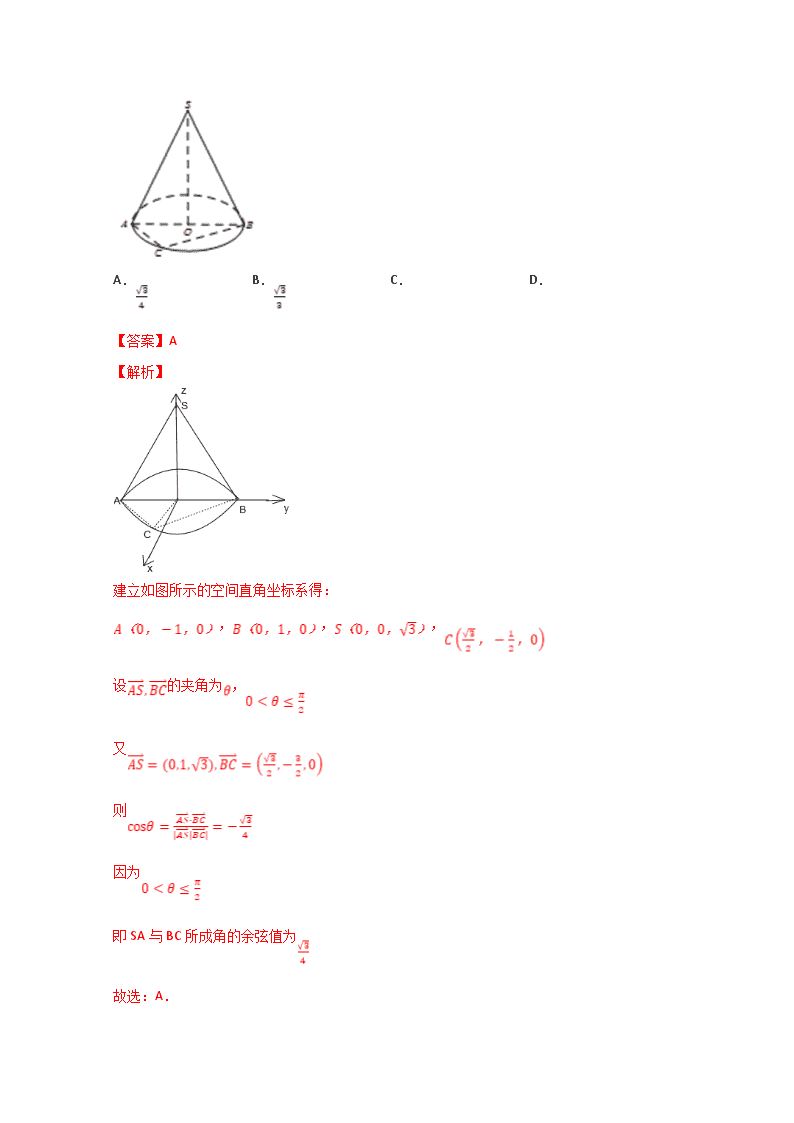
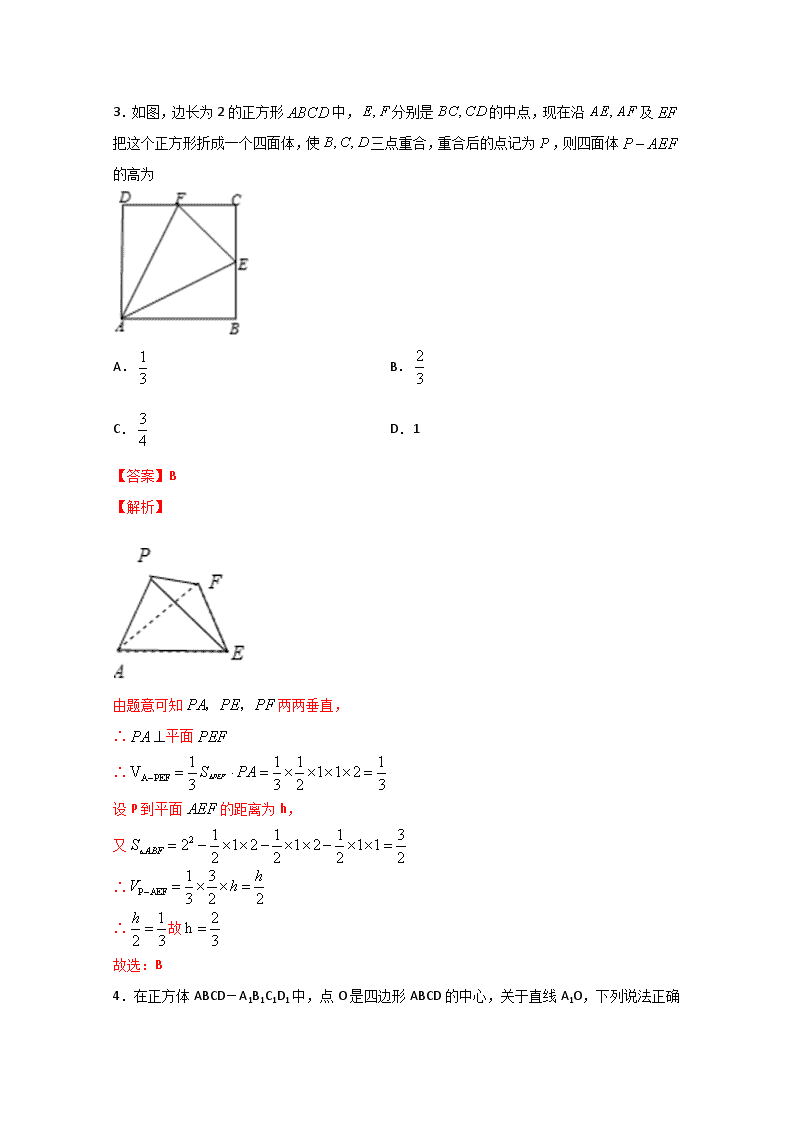
立体几何与空间向量（理科数学） 章节验收测试卷B卷 姓名 班级 准考证号 1．平面四边形中，，，且，现将沿对角线翻折成，则在折起至转到平面的过程中，直线与平面所成最大角的正切值为（ ）‎ A．2 B． C． D．‎ ‎【答案】D ‎【解析】‎ 取BD的中点O,则即平面,从而平面平面,因此在平面的射影在直线上，即为直线与平面所成角，因为，，且，所以,即最大值为，因此直线与平面所成最大角的正切值为，选D.‎ ‎ 2．如图圆锥的高，底面直径是圆上一点，且，则与所成角的余弦值为（　　）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】‎ 建立如图所示的空间直角坐标系得：‎ ‎，，，‎ 设的夹角为， ‎ 又 ‎ 则 ‎ 因为 即SA与BC所成角的余弦值为 故选：A． ‎ ‎3．如图，边长为2的正方形中，分别是的中点，现在沿及把这个正方形折成一个四面体，使三点重合，重合后的点记为，则四面体的高为 A． B．‎ C． D．1‎ ‎【答案】B ‎【解析】‎ 由题意可知两两垂直，‎ ‎∴平面 ‎∴ ‎ 设P到平面的距离为h，‎ 又 ‎∴‎ ‎∴故 ‎ 故选：B 4．在正方体ABCD－A1B‎1C1D1中，点O是四边形ABCD的中心，关于直线A1‎ O，下列说法正确的是（ ）‎ A．A1O∥DC B．A1O⊥BC C．A1O∥平面BCD D．A1O⊥平面ABD ‎【答案】C ‎【解析】‎ ‎∵由异面直线的判定定理可得A1O与DC是异面直线，故A错误；‎ 假设A1O⊥BC，结合A‎1A⊥BC可得BC⊥A1ACC1，则可得BC⊥AC，显然不正确，故假设错误，即B错误；‎ ‎∵在正方体ABCD﹣A1B‎1C1D1中，点O是四边形ABCD的中心，‎ ‎∴A1D∥B‎1C，OD∥B1D1，‎ ‎∵A1D∩DO＝D，B1D1∩B‎1C＝B1，‎ ‎∴平面A1DO∥平面B1CD1，‎ ‎∵A1O⊂平面A1DO，∴A1O∥平面B1CD1．故C正确；‎ 又A‎1A⊥平面ABD，过一点作平面ABD的垂线有且只有一条，则D错误，‎ 故选：C．‎ ‎ 5．某几何体的三视图如图所示，则该几何体的表面积为（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】‎ 由三视图知，该几何体的直观图为多面体，如图所示 其中四边形是边长为4的正方形，所以，‎ 四边形和为全等的直角梯形，‎ 所以，，‎ 四边形是菱形，其对角线长分别为和，‎ 所以，‎ 所以该几何体的表面积为，故选C.‎ ‎ 6．在三棱锥中，面，则三棱锥的外接球表面积是（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】‎ 因为面，所以，又，‎ 解得：，又，满足，所以.‎ 由此可得三棱锥是长方体中的一个几何体，如下图：‎ 长方体的外接球就是三棱锥的外接球，‎ 长方体的体对角线长就是外接球的直径，即，‎ 所以三棱锥的外接球表面积是：‎ 故选B 7．一个动点从正方体的顶点处出发，经正方体的表面，按最短路线到达顶点位置，则下列图形中可以表示正方体及动点最短路线的正视图是（ ）‎ A．①② B．①③ C．②④ D．③④‎ ‎【答案】C ‎【解析】‎ 由点A经正方体的表面，按最短路线爬行到定点位置，共有6种展开方式，‎ 若把平面和平面展开到同一个平面内，在矩形中连接会经过的中点，故此时的正视图为②；‎ 若把平面和平面展到同一个平面内，在矩形中连接会经过的中点，此时的正视图为④‎ 其中其它几种展开方式所对应的正视图在题中没有出现或已在②④中，故选C. 8．已知，, 为三条不同的直线，，，为三个不同的平面，则下列说法正确的是（ ）‎ A．若，，则 B．若，，，则 C．若，，则 D．若，，，，则 ‎【答案】D ‎【解析】‎ A, 若，,则或，故A不正确.‎ B, 若，，，则或与相交，故B不正确.‎ C，若，，则或，故C不正确.‎ D,如图，由可得，易证，故D正确.‎ ‎ 9．已知点在同一个球的球面上，，若四面体外接球的球心恰好在侧棱上，，则四面体的体积为（　　）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】‎ 由，可知，‎ 取的中点，则点为外接圆的圆心，又为四面体外接球球心，‎ 所以平面，且为的中位线，‎ 所以平面，‎ 故三棱锥的体积为．‎ 故选：C． 10．如图，网格纸上小正方形的边长为1,粗线画出的是某四棱锥的三视图，则该四棱锥的体积为( )‎ A．6 B．‎8 ‎C． D．‎ ‎【答案】B ‎【解析】‎ 由三视图可得四棱锥为如图所示的长方体中的四棱锥，其中在长方体中，，点分别为的中点．‎ 由题意得，所以可得，‎ 又，‎ 所以平面 即线段即为四棱锥的高．‎ 所以.‎ 故选B． 11．如图所示，边长为a的空间四边形ABCD中，∠BCD＝90°，平面ABD⊥平面BCD，则异面直线AD与BC所成角的大小为（　　）‎ A．30° B．45° C．60° D．90°‎ ‎【答案】C ‎【解析】‎ 由题意得BC＝CD＝a，∠BCD＝90°，‎ ‎∴BD＝，∴∠BAD＝90°，‎ 取BD中点O，连结AO，CO，‎ ‎∵AB＝BC＝CD＝DA＝a，‎ ‎∴AO⊥BD，CO⊥BD，且AO＝BO＝OD＝OC＝，‎ 又∵平面ABD⊥平面BCD，平面ABD∩平面BCD＝BD，AO⊥BD，‎ ‎∴AO⊥平面BCD，‎ 延长CO至点E，使CO＝OE，连结ED，EA，EB，‎ 则四边形BCDE为正方形，即有BC∥DE，‎ ‎∴∠ADE（或其补角）即为异面直线AD与BC所成角，‎ 由题意得AE＝a，ED＝a，‎ ‎∴△AED为正三角形，∴∠ADE＝60°，‎ ‎∴异面直线AD与BC所成角的大小为60°．‎ 故选：C．‎ ‎ 12．如图，在正方体，点在线段上运动，则下列判断正确的是（ ）‎ ‎①平面平面 ‎②平面 ‎③异面直线与所成角的取值范围是 ‎④三棱锥的体积不变 A．①② B．①②④ C．③④ D．①④‎ ‎【答案】C ‎【解析】‎ 对于①，连接DB1，根据正方体的性质，有DB1⊥面ACD1 ，DB1⊂平面PB1D，从而可以证明平面PB1D⊥平面ACD1，正确．‎ ‎②连接A1B，A‎1C1容易证明平面BA‎1C1∥面ACD1，从而由线面平行的定义可得 A1P∥平面ACD1，正确．‎ ‎③当P与线段BC1的两端点重合时，A1P与AD1所成角取最小值，‎ 当P与线段BC1的中点重合时，A1P与AD1所成角取最大值，‎ 故A1P与AD1所成角的范围是，错误；‎ ‎④=，C到面AD1P的距离不变，且三角形AD1P的面积不变．‎ ‎∴三棱锥A﹣D1PC的体积不变，正确；‎ 正确的命题为①②④．‎ 故选：B．‎ ‎ 13．如图，在四棱锥中，底面四边形是矩形，，是等边三角形，平面平面，点，分别在线段，上，若平面，且，则点到平面的距离为_____．‎ ‎【答案】‎ ‎【解析】‎ 取AD的中点为，过点作的平行线 因为是等边三角形，‎ 所以，‎ 平面平面，‎ 平面平面，‎ 平面，‎ 所以平面，‎ 故垂直于，‎ 又垂直于，‎ 故以为原点，为轴，过点作的平行线为轴，为轴，建立空间直角坐标系，‎ 设，，，，，，‎ 设，，，‎ 则，‎ ‎∴，，‎ 设平面的法向量，‎ 则，‎ 解得，，‎ 取，得，‎ ‎∵平面，‎ ‎∴，‎ 解得，‎ ‎∴点到平面的距离.‎ 故答案为：． 14．已知正三棱柱底面边长为，高为3，圆是三角形的内切圆，点 是圆上任意一点，则三棱锥的外接球的体积为__________．‎ ‎【答案】‎ ‎【解析】‎ ‎∵正三棱柱底面边长为，‎ ‎∴等边三角形的内切圆的半径为，‎ 的外接圆的半径为．‎ 设球心到上下底面的距离分别为，，‎ 则，解得．‎ ‎∴．‎ 则三棱锥的外接球的体积为． 15．如图，正方体的棱长为，动点在对角线上，过点作垂直于的平面，记这样得到的截面多边形（含三角形）的周长为，设，则当时，函数的值域为______．‎ ‎【答案】‎ ‎【解析】‎ 当时，截面多边形是六边形HIJKLM，‎ 设==λ，则==1﹣λ，‎ ‎∴HI+IJ=，‎ ‎∴截面六边形的周长为；‎ 故答案为： 16．类比圆的内接四边形的概念，可得球的内接四面体的概念.已知球的一个内接四面体中，，过球心，若该四面体的体积为1，且，则球的表面积的最小值为______.‎ ‎【答案】‎ ‎【解析】‎ 设,结合体积为1时,,故所以,所以,结合 ‎,建立方程,得到,令 ‎,结合二次函数的性质可知在递减,递增 令,结合复合函数的单调性可知,在递增,在递减,而始终递减,故在递减,在递增,故当,取到最小值为38‎ 所以面积最小值为 17．如图，在三棱柱中，平面，是的中点，，，.‎ ‎（1）证明：；‎ ‎（2）若，求二面角的余弦值.‎ ‎【答案】（1）证明见解析；（2）.‎ ‎【解析】‎ ‎（1）证明：连接，，‎ 因为在中，，，．‎ 所以．‎ 所以，‎ 因为．‎ 所以，‎ 又平面，且平面，‎ 所以，，‎ 所以平面，‎ 因为平面，‎ 所以．‎ ‎（2）以为原点建立如图所示空间直角坐标系，‎ 则，，，，‎ 所以，，，‎ 设平面的法向量为，设平面的法向量为，‎ 则，取，‎ 则，‎ 取．‎ 所以，‎ 即二面角的平面角的余弦值为． 18．如图，已知四棱锥中，四边形为矩形，，，.‎ ‎（1）求证：平面；‎ ‎（2）设，求平面与平面所成的二面角的正弦值.‎ ‎【答案】（1）见证明；（2）‎ ‎【解析】‎ ‎（1）证明： BCSD ，BCCD 则BC平面SDC, 又 则AD平面SDC，平面SDC ‎ SCAD 又在△SDC中，SC=SD=2, DC=AB，故SC2+SD2=DC2‎ 则SCSD ，又 所以 SC平面SAD ‎ ‎（2）解：作SOCD于O，因为BC平面SDC,‎ 所以平面ABCD平面SDC，故SO平面ABCD 以点O为原点，建立坐标系如图. ‎ 则S(0,0,),C(0，,0), A(2，-,0),B(2，,0) ‎ 设E(2,y,0),因为 所以 即E((2,,0) ‎ 令，则，‎ ‎，令，则，‎ 所以所求二面角的正弦值为 19．在五边形AEBCD中，，C，，，（如图）.将△ABE沿AB折起，使平面ABE⊥平面ABCD，线段AB的中点为O(如图）.‎ ‎（1）求证：平面ABE⊥平面DOE；‎ ‎（2）求平面EAB与平面ECD所成的锐二面角的大小.‎ ‎【答案】（1）见解析（2）45°‎ ‎【解析】‎ ‎（1）由题意，O是线段AB的中点，则.‎ 又，则四边形OBCD为平行四边形，又，则，‎ 因，，则.‎ ‎，则AB⊥平面EOD.‎ 又平面ABE，故平面ABE⊥平面EOD. ‎ ‎（2）由（1）易知OB，OD，OE两两垂直，以O为坐标原点，以OB，OD，OE所在直线分别为轴建立如图所示的空间直角坐标系，‎ ‎△EAB为等腰直角三角形，且AB=2CD=2BC，‎ 则，取，‎ 则O（0，0，0），A（-1，0，0），B（1，0，0），C（1，1，0），D（0，1，0），‎ E（0，0，1），则，，‎ 设平面ECD的法向量为，‎ 则有取，得平面ECD的一个法向量，‎ 因OD⊥平面ABE.则平面ABE的一个法向量为，‎ 设平面ECD与平面ABE所成的锐二面角为θ，则 ‎，‎ 因为，所以，‎ 故平面ECD与平面ABE所成的镜二面角为45°. ‎ ‎ 20．如图，在以为顶点的五面体中，面为正方形，，，且二面角与二面角都是.‎ ‎（1）证明：平面；‎ ‎（2）求直线与平面所成角的正弦值.‎ ‎【答案】（1）证明见解析；‎ ‎（2）.‎ ‎【解析】‎ ‎（1）面ABEF为正方形 又，而,‎ 面,面 面 ‎（2），则由（1）知面平面，过作，垂足为，平面．‎ 以为坐标原点，的方向为轴正方向，为单位长度，建立如图所示的空间直角坐标系． ‎ 由（1）知为二面角的平面角，故，又，则，，，，． ‎ 由已知，，平面．又平面平面，‎ 故，．由，可得平面，‎ 为二面角的平面角，．．‎ ‎，，．‎ 设是平面的法向量，则，即，‎ 可取 . ‎ 则．‎ 直线与平面BCE所成角的正弦值为 . ‎ ‎ 21．如图，四棱锥P-ABCD中，底面ABCD是边长为3的菱形，∠ABC=60°．PA⊥面ABCD，且PA=3．F在棱PA上，且AF=1，E在棱PD上．‎ ‎（Ⅰ）若CE∥面BDF，求PE：ED的值；‎ ‎（Ⅱ）求二面角B-DF-A的大小．‎ ‎【答案】（Ⅰ）见解析；（Ⅱ）arctan ‎【解析】‎ ‎（Ⅰ）过E作EG∥FD交AP于G，连接CG，连接AC交BD于O，连接FO．‎ ‎∵EG∥FD，EG⊄面BDF，FD⊂面BDF，∴EG∥面BDF，又EG∩CE=E，CE∥面BDF，EG，CE⊂面CGE，‎ ‎∴面CGE∥面BDF，又CG⊂面CGE，∴CG∥面BDF，‎ 又面BDF∩面PAC=FO，CG⊂面PAC，∴FO∥CG．‎ 又O为AC中点，∴F为AG中点，且AF=1，∴AF=FG=1，∵PA=3，∴FG=GP=1，‎ ‎∴E为PD中点，PE：ED=1：1．‎ ‎（Ⅱ）过点B作BH⊥直线DA交DA延长线于H，过点H作HI⊥直线DF交DF于I，‎ ‎∵PA⊥面ABCD，∴面PAD⊥面ABCD，∴BH⊥面PAD，由三垂线定理可得DI⊥IB，‎ ‎∴∠BIH是二面角B-DF-A的平面角．由题易得AH=，BH=，HD=，‎ 且=，∴HI=，∴tan∠BIH=×=，‎ ‎∴二面角B-DF-A的大小为arctan．‎ ‎ 22．如图，矩形所在平面，，、分别是、的中点.‎ ‎（1）求证：平面平面；‎ ‎（2）若直线与平面所成角的正弦值为，求二面角的正弦值.‎ ‎【答案】（1）见解析（2）‎ ‎【解析】‎ 如图，取中点，连接，.‎ ‎（1）证明：∵，，为中点，‎ ‎∴，，‎ ‎∴是平行四边形，，‎ 又∵，，‎ ‎∴面，∴面面.‎ ‎∵，为中点，面，‎ ‎∴面，∵面，‎ ‎∴平面平面.‎ ‎（2）建立如图所示坐标系，‎ ‎，，，，，，.‎ 由（1）知面，‎ ‎∴，.‎ ‎∵直线与平面所成角的正弦值为，‎ ‎∴由得.‎ 设为面的法向量，则，.‎ 由得，，‎ ‎∵面，，设二面角为，为锐角，‎ 则，‎ ‎∴. ‎