- 2021-06-24 发布 |
- 37.5 KB |
- 5页

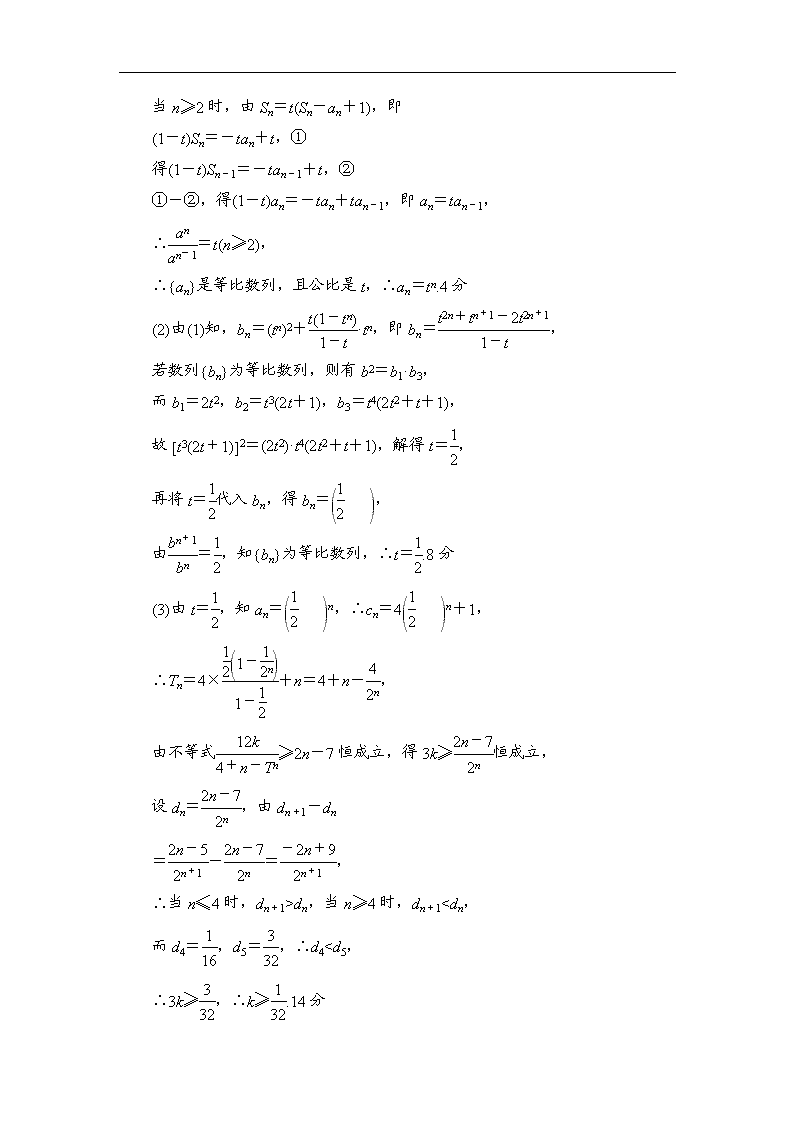

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学 17-18版 第7章 热点探究训练4
热点探究训练(四) A组 基础过关 1.(2017·苏州期中)设数列{an}的前n项和为Sn,满足2Sn=an+1-2n+1+1,且a1,a2+5,a3成等差数列. (1)求a1,a2的值; (2)求证:数列{an+2n}是等比数列,并求数列{an}的通项公式. [解] (1)由已知,得2a1=a2-3 ①, 2(a1+a2)=a3-7 ②, 又因为a1,a2+5,a3成等差数列, 所以a1+a3=2a2+10 ③, 解①②③,得a1=1,a2=54分 (2)由已知,n∈N+时,2(Sn+1-Sn)=an+2-an+1-2n+2+2n+1, 即an+2=3an+1+2n+1, 即an+1=3an+2n(n≥2),8分 由(1)得,a2=3a1+2,∴an+1=3an+2n(n∈N+). 从而有an+1+2n+1=3an+2n+2n+1=3an+3×2n=3(an+2n). 又a1+2>0,∴an+2n>0,∴=3. ∴数列{an+2n}是等比数列,且公比为3. ∴an+2n=(a1+2)×3n-1=3n,即an=3n-2n.14分 2.(2017·泰州中学高三模底考试)已知数列{an}的前n项和Sn满足:Sn=t(Sn-an+1)(t为常数,且t≠0,t≠1). (1)求{an}的通项公式; (2)设bn=a+Sn·an,若数列{bn}为等比数列,求t的值; (3)在满足条件(2)的情形下,设cn=4an+1,数列{cn}的前n项和为Tn,若不等式≥2n-7对任意的n∈N+恒成立,求实数k的取值范围. 【导学号:62172212】 [解] (1)当n=1时,S1=t(S1-a1+1),得a1=t. 当n≥2时,由Sn=t(Sn-an+1),即 (1-t)Sn=-tan+t,① 得(1-t)Sn-1=-tan-1+t,② ①-②,得(1-t)an=-tan+tan-1,即an=tan-1, ∴=t(n≥2), ∴{an}是等比数列,且公比是t,∴an=tn.4分 (2)由(1)知,bn=(tn)2+·tn,即bn=, 若数列{bn}为等比数列,则有b=b1·b3, 而b1=2t2,b2=t3(2t+1),b3=t4(2t2+t+1), 故2=(2t2)·t4(2t2+t+1),解得t=, 再将t=代入bn,得bn=, 由=,知{bn}为等比数列,∴t=.8分 (3)由t=,知an=n,∴cn=4n+1, ∴Tn=4×+n=4+n-, 由不等式≥2n-7恒成立,得3k≥恒成立, 设dn=,由dn+1-dn =-=, ∴当n≤4时,dn+1>dn,当n≥4时,dn+1查看更多