高中数学：《绝对值不等式的解法》课件（新人教a版选修4-5）

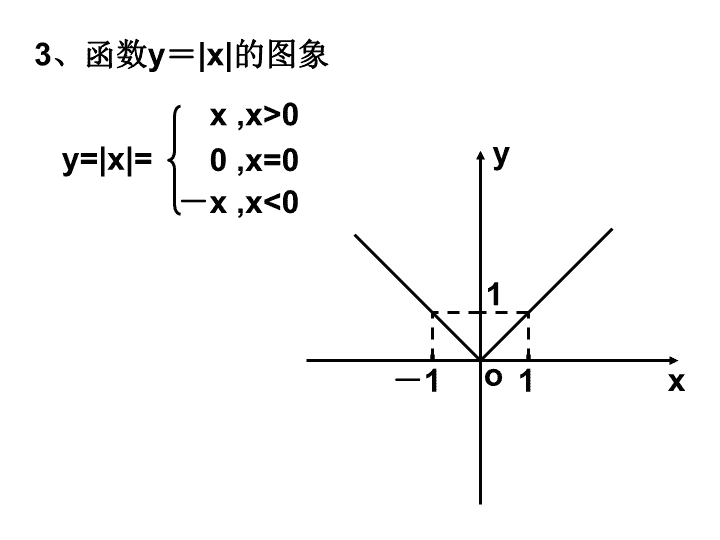
高中数学：《绝对值不等式的解法》课件（新人教a版选修4-5）

绝对值不等式的解法（一） 授课人：陈晓琳 一、知识联系 1 、绝对值的定义 |x|= x ,x>0 － x ,x<0 0 ,x=0 2 、绝对值的几何意义 0 x |x| x 1 x |x － x 1 | 3 、函数 y ＝ |x| 的图象 y=|x|= x ,x>0 － x ,x<0 0 ,x=0 o x y 1 1 － 1 二、探索解法 探索：不等式 |x|<1 的解集。 方法一： 利用绝对值的几何意义观察 方法二： 利用绝对值的定义去掉绝对值符号，需要分类讨论 方法三： 两边同时平方去掉绝对值符号 方法四： 利用函数图象观察 这是解含绝对值不等式的四种常用思路 1 2 3 4 0 -1 不等式 |x|<1 的解集表示到原点的距离小于 1 的点的集合。 1 所以，不等式 |x|<1 的解集为 {x|-1a (a>0) 的解集。 ① 不等式 |x|a 的解集为 {x|x<-a 或 x>a } 0 -a a 0 -a a 基础练习： 解下列不等式： （ 1 ） |x|>5 （ 2 ） 2|x|<5 （ 3 ） |2x|>5 （ 4 ） |x-1|<5 （ 5 ） |2x-1|<5 （ 6 ） |2x 2 -x|<1 （ 7 ） |2 x -1|<1 1 － 4 6 （ 4 ） |x-1|<5 （ 5 ） |2x-1|<5 － 2 3 解下列不等式： 巩固练习： （ 8 ） | 6 - |2 x +1| | >1 三、本节小结 本节课我们通过求不等式 |x|<1 的解集，得到了解含绝对值不等式的四种常用思路。 这四种思路将有助于我们有效地解决含绝对值不等式的问题。 方法一： 利用绝对值的几何意义观察 方法二： 利用绝对值的定义去掉绝对值符号，需要分类讨论 方法三： 两边同时平方去掉绝对值符号 方法四： 利用函数图象观察 谢谢！