2019-2020学年四川省三台中学高一上学期第三次月考数学试题 含答案

2019-2020学年四川省三台中学高一上学期第三次月考数学试题 含答案

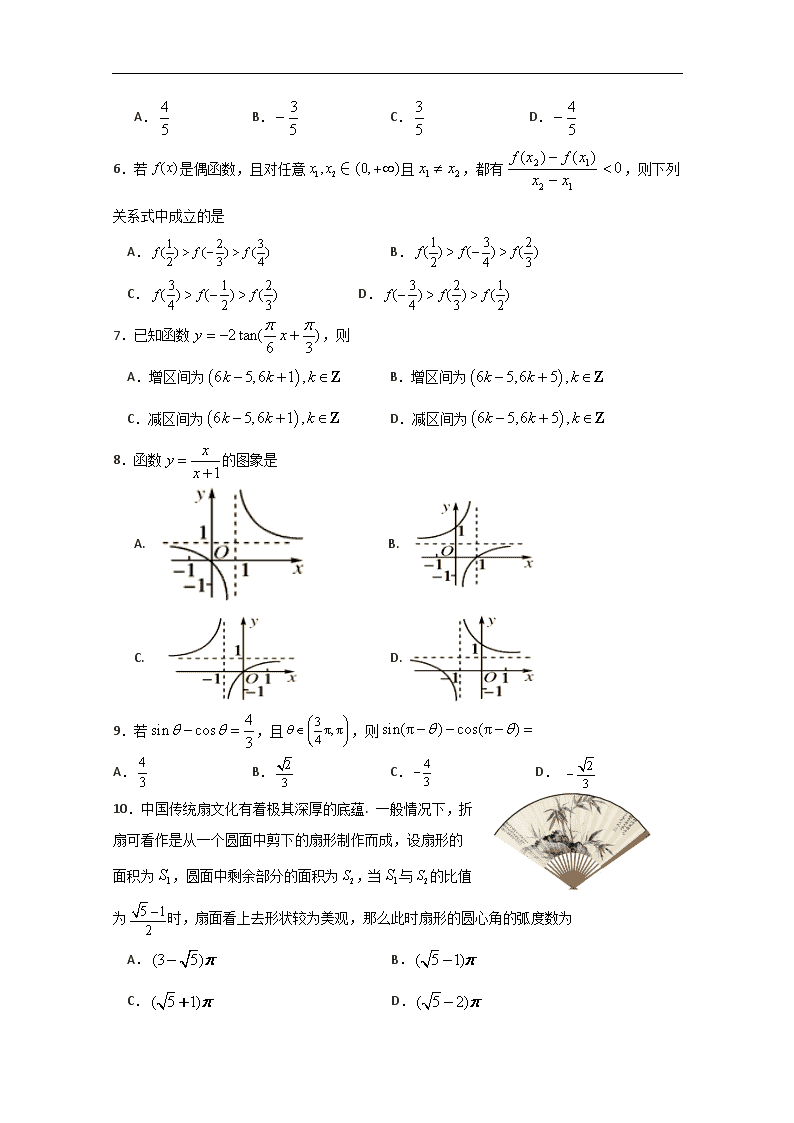
保密 ★启用前 ‎ 三台中学2019级高一上期第三次学月考试 数学试题 考试时间：100分钟 ‎ 本试卷分为试题卷和答题卡两部分，其中试题卷由第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）组成，共4页；答题卡共4页．满分100分，考试时间100分钟．‎ 注意事项：‎ ‎1．答题前，考生务必将自己的学校、班级、姓名用0.5毫米黑色签字笔填写清楚，同时用2B铅笔将考号准确填涂在“考号”栏目内．‎ ‎2．选择题使用2B铅笔填涂在答题卡对应题目标号的位置上，如需改动，用橡皮擦擦干净后再选涂其它答案；非选择题用0.5毫米黑色签字笔书写在答题卡的对应框内，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效．‎ 第Ⅰ卷（选择题，共48分）‎ 一、 选择题：本大题共12小题，每小题4分，共48分．在每小题给出的四个选项中，只有一个是符合题目要求的．‎ ‎1. ‎ A． B． C． D． ‎ ‎2.已知幂函数的图像过点，则 ‎ A． B． C． D． ‎ ‎3．已知集合，非空集合满足，则集合有 A．1个 B．2个 C．3个 D．4个 ‎4．下列各对函数中，图象完全相同的是 A．与 B. 与 C．与 D．与 ‎5．设角的终边上一点P的坐标是，则等于 A． B． C． D．‎ ‎6．若是偶函数，且对任意∈且，都有，则下列关系式中成立的是 A． B．‎ C． D．‎ ‎7．已知函数，则 ‎ A．增区间为 B．增区间为 C．减区间为 D．减区间为 ‎8．函数的图象是 ‎ A. B. ‎ C. D. ‎ ‎9．若，且，则 A． B． C． D． ‎ ‎10．中国传统扇文化有着极其深厚的底蕴. 一般情况下，折扇可看作是从一个圆面中剪下的扇形制作而成，设扇形的面积为，圆面中剩余部分的面积为，当与的比值为时，扇面看上去形状较为美观，那么此时扇形的圆心角的弧度数为 A． B． ‎ C． D．‎ ‎11．设函数，若，则 A． B． C． D． ‎ ‎12．设函数是定义在上的偶函数，对任意，都有，且当时，，若在区间内关于的方程（a>1）至少有2个不同的实数根，至多有3个不同的实数根，则的取值范围是 A. B. C. D. ‎ 第Ⅱ卷（非选择题，共52分）‎ 一、 填空题：本大题共4小题，每小题3分，共12分．把答案直接填在答题卡中的横线上．‎ ‎13．已知函数的图象过定点P，则点P的坐标为_______.‎ ‎14．已知，则_________‎ ‎15． ______.‎ ‎16．函数的图像与函数的图像的所有交点为，则_______‎ 二、 解答题：本大题共4小题，每小题10分，共40分．解答应写出文字说明．证明过程或演算步骤．‎ ‎17.已知集合，‎ ‎（Ⅰ）求 及；‎ ‎（Ⅱ）若，且，求实数的取值范围.‎ ‎18．已知函数．‎ ‎（1）求函数的最小正周期和对称轴方程；‎ ‎（2）讨论函数在上的单调性．‎ ‎19．近年来大气污染防治工作得到各级部门的重视，某企业现有设备下每日生产总成本（单位：万元）与日产量（单位：吨）之间的函数关系式为，现为了配合环境卫生综合整治，该企业引进了除尘设备，每吨产品除尘费用为万元，除尘后当日产量时，总成本.‎ ‎（1）求的值；‎ ‎（2）若每吨产品出厂价为59万元，试求除尘后日产量为多少时，每吨产品的利润最大，最大利润为多少？‎ ‎20．已知函数是上的奇函数。‎ ‎（1）求的值；‎ ‎（2）判断函数的单调性并给出证明；‎ ‎（3）若时恒成立，求的最大值.‎ ‎ ‎ 三台中学2019级高一上期第三次学月考试 数学参考答案 一选择题： 1—5．BDCCB 6—10．ACCDA 11—12 BD ‎12.解:对都有，所以是定义在上的周期为4的函数 作函数与的图象，结合图象可知，解得，‎ 二、填空题： 13． 14． 15． 16．‎ ‎16详解：如下图，画出函数 和 的图象，可知有4个交点，并且关于点 对称，所以 ， ，所以 .‎ 三：解答题 ‎17．解：（Ⅰ）解：，；‎ ‎∴ …………………………………………2分 ‎∵ ‎ ‎∴. …………………………………………5分 ‎（Ⅱ）∵故 …………………………6分 ‎∴当时成立，则； …………………………8分 当时，则； …………………………9分 综上所述，实数的取值范围是. …………………………10分 ‎18．解：（1） ， ……………………3分 因为，所以最小正周期， ……………………4分 令，所以对称轴方程为，．………5分 ‎（2）令， ………6分 得，， ………7分 设，，‎ 易知， ………………………………8分 所以，当时，在区间上单调递增；在区间上单调递减． ………………………………10分 ‎19．‎ 解：（1）由题意，除尘后，‎ ‎…………3分 当日产量时，总成本，‎ 故，‎ 解得. …………5分 ‎（2）由（1），‎ 总利润，………7分 每吨产品的利润，………8分 当且仅当，即时取等号，‎ 除尘后日产量为11吨时，每吨产品的利润最大，最大利润为6万元.‎ ‎ ……10分 ‎20．解：‎ ‎（1）∵是上的奇函数,∴,即故.‎ ‎……1分 ‎（2）不论为何实数,在定义域上单调递增. ……2分 ‎ ‎ 证明：设,则,, ……3分 由,∴,所以,,,‎ 所以,所以由定义可知,不论为何实数,在定义域上单调递增. ……5分 ‎（3）由条件可得：,即 ……6分 即恒成立, ……7分 ‎∴的最小值, ……8分 设,因为,故,又函数在上单调递减,在上单调递增，所以的最小值是, ……9分 所以,即的最大值是 ……10分 ‎ ‎