2019-2020学年宁夏石嘴山市第三中学高一上学期期中数学试题（解析版）

2019-2020学年宁夏石嘴山市第三中学高一上学期期中数学试题（解析版）

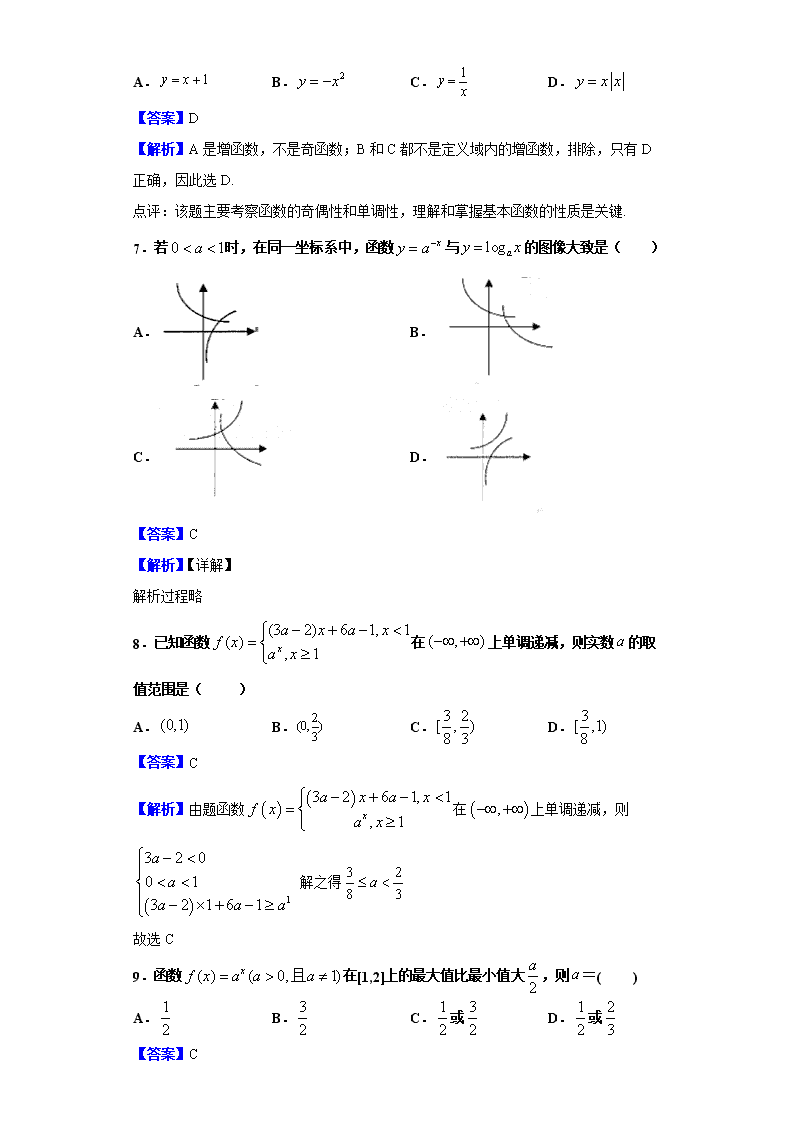
‎2019-2020学年宁夏石嘴山市第三中学高一上学期期中数学试题 一、单选题 ‎1．全集U={1，2，3，4，5，6}，集合A={1，2，5}，集合B={3，4，5}，则（∁UA）∩B等于 A．{4} B．{3，4} C．{2，3，4} D．{3}‎ ‎【答案】B ‎【解析】根据交集、补集的定义，进行交集、补集的运算即可．‎ ‎【详解】‎ 由题意，全集U={1，2，3，4，5，6}，集合A={1，2，5}，‎ ‎∴∁UA={3，4，6}，∴（∁UA）∩B={3，4，6}∩{3，4，5}={3，4}．故选B．‎ ‎【点睛】‎ 本题考查列举法表示集合的概念，以及补集和交集的运算．‎ ‎2．下列等式成立的是( )．‎ A．log2(8－4)＝log2 8－log2 4 B．＝‎ C．log2 23＝3log2 2 D．log2(8＋4)＝log2 8＋log2 4‎ ‎【答案】C ‎【解析】根据对数的运算性质进行分析、判断即可得到答案．‎ ‎【详解】‎ 根据对数的运算性质逐个进行判断可得，选项A,B,D都不符合对数的运算性质，选项C符合．所以C正确．‎ 故选C．‎ ‎【点睛】‎ 解答本题时容易出现错误，解题的关键是记清对数的三个运算性质及换底公式，属于基础题．‎ ‎3．已知函数f（x）=2x的反函数为y=g（x），则g（）的值为（　　）‎ A． B．1 C．12 D．2‎ ‎【答案】A ‎【解析】由已知函数解析式求得，再把与互换可得原函数的反函数，取得答案．‎ ‎【详解】‎ 解：∵由，得 ‎∴原函数的反函数为， ‎ 则．‎ 故选：A．‎ ‎【点睛】‎ 本题考查函数的反函数的求法，是基础题．‎ ‎4．下列函数中与函数y=x相等的函数是（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】函数的定义域为 ，而函数的定义域为 故函数与函数不相等；‎ 函数 ，故函数与函数不相等；‎ 函数的定义域为，而函数的定义域为 故函数与函数不相等；‎ 函数的定义域为，且,故函数 与函数相等.‎ 选D ‎5．三个数之间的大小关系是（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】 ，则 ‎ 故 选B ‎6．下列函数中，既是奇函数又是增函数的为（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】A是增函数，不是奇函数；B和C都不是定义域内的增函数，排除，只有D正确，因此选D.‎ 点评：该题主要考察函数的奇偶性和单调性，理解和掌握基本函数的性质是关键.‎ ‎7．若时，在同一坐标系中，函数与的图像大致是（ ）‎ A． B．‎ C． D．‎ ‎【答案】C ‎【解析】【详解】‎ 解析过程略 ‎8．已知函数在上单调递减，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】由题函数在上单调递减，则 解之得 ‎ 故选C ‎9．函数在[1,2]上的最大值比最小值大，则＝(　 　)‎ A． B． C．或 D．或 ‎【答案】C ‎【解析】对a分类讨论，根据指数函数的单调性布列方程，解之即可.‎ ‎【详解】‎ 当a＞1时，函数f（x）=ax（a＞0且a≠1）在区间[1，2]上是增函数，由题意可得 a2﹣a=，∴a=．‎ 当0＜a＜1时，函数f（x）=ax（a＞0且a≠1）在区间[1，2]上是减函数，由题意可得 a﹣a2=，解得 a=．‎ 综上，a的值为或 故选：C．‎ ‎【点睛】‎ 本题主要考查指数函数的单调性和最值，体现了分类讨论的数学思想，属于基础题．‎ ‎10．在下列区间中，函数的零点所在的区间为（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】先判断函数在上单调递增，由,利用零点存在定理可得结果.‎ ‎【详解】‎ 因为函数在上连续单调递增，‎ 且,‎ 所以函数的零点在区间内，故选C.‎ ‎【点睛】‎ 本题主要考查零点存在定理的应用，属于简单题.应用零点存在定理解题时，要注意两点：（1）函数是否为单调函数；（2）函数是否连续.‎ ‎11．已知是定义在上的偶函数，当时， ，则不等式 的解集为 A． B． C． D．‎ ‎【答案】C ‎【解析】当时， ，∴f(1)=0，‎ 又∵当x∈[0,+∞)时,f(x)为增函数，又是定义在R上的偶函数，‎ 故f(x)>0时，x>1，或x<−1，‎ 故时,>1,或 <−1，‎ 解得：x∈，‎ 故选：C 点睛：解抽象不等式的常规思路为借助单调性把问题转化为具体不等式的解法问题，在本题中，函数为偶函数，利用图象的对称性，在y轴两侧分别处理不等式即可.‎ ‎12．设函数满足对任意的都有且，则（ ）‎ A．2011 B．2010 C．4020 D．4022‎ ‎【答案】C ‎【解析】 原式 ，故选C. ‎ 二、填空题 ‎13．已知关于的函数是幂函数，则__________．‎ ‎【答案】‎ ‎【解析】关于的函数是幂函数，则 .‎ ‎14．函数（，）的图象必过定点，点的坐标为 ‎__________．‎ ‎【答案】(2,2)‎ ‎【解析】函数 的图象可以看作把 的图象向右平移一个单位再向上平移2个单位而得到， 且一定过点 ， 则 应过点 故答案为 ‎【点睛】本题考查的知识点是指数函数的图象与性质，其中根据函数的解析式，结合函数图象平移变换法则，求出平移量是解答本题的关键．‎ ‎15．方程有解，则实数的取值范围为_________..‎ ‎【答案】‎ ‎【解析】将原方程转化为，根据函数的奇偶性画出函数的图像，由与有交点列不等式，解不等式求得的取值范围.‎ ‎【详解】‎ 原方程可化为.函数为偶函数，图像关于轴对称，当时，为减函数.由此画出函数的图像如下图所示，由图可知，要使与有交点，则需，解得.‎ 故答案为：.‎ ‎【点睛】‎ 本小题根据方程有解求参数的取值范围，考查函数与方程，考查化归与转化的数学思想方法，考查数形结合的数学思想方法，属于基础题.‎ ‎16．设函数的定义域为，值域为，若的最小值为，则实数的值是_____________。‎ ‎【答案】或 ‎【解析】根据题意，利用函数图像的变换，作出的图像，根据图像特点，结合题意，分和进行讨论，列出关于的等式关系，即可求解出结果。‎ ‎【详解】‎ 如图所示，做出的图像，‎ 若，当时，时，。‎ 若时， 当时，，。‎ 综上所述，或。‎ ‎【点睛】‎ 本题主要考查了对数函数的图像以及性质，在画对数函数图像时要注意强化讨论意识，对底数是还是进行讨。作的图像，应先作出的图像，轴上方的图像保留，轴下方的图像翻折。‎ 三、解答题 ‎17．已知集合，.‎ ‎（1）求 ‎（2）求.‎ ‎【答案】（1）＜；（2）‎ ‎【解析】（1）先解指数不等式得集合A，再解对数不等式得集合B，最后根据交集定义得结果，（2）先根据补集定义求，再根据并集定义得结果.‎ ‎【详解】‎ ‎（1）由得，故；‎ 由＞得＞，故＞‎ ‎∴＜‎ ‎（2）由＞得 ‎∴‎ ‎【点睛】‎ 本题考查指数不等式、对数不等式以及集合交并补运算，考查基本求解能力，属基础题.‎ ‎18．求值：‎ ‎(1) ； ‎ ‎(2).‎ ‎【答案】（1）；（2）.‎ ‎【解析】（1）直接利用根式与分数指数幂的运算法则求解即可,化简过程注意避免出现符号错误；（2）直接利用对数的运算法则求解即可，解答过程注意避免出现计算错误.‎ ‎【详解】‎ ‎(1) ‎ ‎;‎ ‎(2)‎ ‎.‎ ‎【点睛】‎ 本题主要考查对数的运算与指数的运算，属于中档题. 指数幂运算的四个原则：（1）有括号的先算括号里的，无括号的先做指数运算；（2）先乘除后加减，负指数幂化成正指数幂的倒数；（3）底数是负数，先确定符号，底数是小数，先化成分数，底数是带分数的，先化成假分数；（4）若是根式，应化为分数指数幂，尽可能用幂的形式表示，运用指数幂的运算性质来解答（化简过程中一定要注意等价性，特别注意开偶次方根时函数的定义域）‎ ‎19．已知函数的图像经过点 ‎(1)求的值并判断的奇偶性；‎ ‎(2)判断并证明函数在的单调性，并求出最大值.‎ ‎【答案】（1），奇函数；（2）函数在上递增，证明见解析，最大值为.‎ ‎【解析】（1）利用点列方程，解方程求得的值.根据函数奇偶性的定义，判断出函数的奇偶性.‎ ‎（2）首先判断出函数在上递增，然后利用单调性的定义，证明出单调性，并根据单调性求得函数的最大值.‎ ‎【详解】‎ ‎（1）由于函数过点，故，所以.函数的定义域为，且，所以函数为奇函数.‎ ‎（2）函数在上递增，证明如下：任取，则，由于，所以，所以函数在上递增，且最大值为.‎ ‎【点睛】‎ 本小题主要求函数解析式，考查函数的奇偶性，考查利用定义证明函数的单调性，考查根据函数的单调性求最值，属于中档题.‎ ‎20．某企业常年生产一种出口产品，根据预测可知，进入2l世纪以来，该产品的产量平稳增长记2009年为第1年，且前4年中，第x年与年产量万件之间的关系如表所示：‎ x ‎1‎ ‎2‎ ‎3‎ ‎4‎ 若近似符合以下三种函数模型之一：．‎ 找出你认为最适合的函数模型，并说明理由，然后求出相应的解析式所求a或b值保留1位小数；‎ 因遭受某国对该产品进行反倾销的影响，2015年的年产量比预计减少，试根据所建立的函数模型，确定2015年的年产量．‎ ‎【答案】（1）最适合的模型解析式为；（2）2015年的实际产量为9.1万件.‎ ‎【解析】试题分析：（1）分别代人不同模型，确定a,b值，再代人第三或四个量验证是否符合（2）先按模型计算2015年的年产量，再计算实际年产量．‎ 试题解析：解：(1)符合条件的是f(x)＝ax＋b.‎ 若模型为f(x)＝2x＋a，则由f(1)＝21＋a＝4，得a＝2，即f(x)＝2x＋2，‎ 此时f(2)＝6, f(3)＝10, f(4)＝18，与已知相差太大，不符合．‎ ‎ 若模型为f(x)＝logx＋a，则f(x)是减函数，与已知不符合．‎ ‎ 由已知得解得 所以f(x)＝x＋，x∈N.‎ ‎(2)2015年预计年产量为f(7)＝×7＋＝13,2015年实际年产量为13×(1－30%)＝9.1，‎ 答：最适合的模型解析式为f(x)＝x＋，x∈N .2015年的实际产量为9.1万件．‎ ‎21．已知函数（为常数且）的图象经过点，‎ ‎（1）试求的值；‎ ‎（2）若不等式在时恒成立，求实数的取值范围.‎ ‎【答案】（1）；（2）.‎ ‎【解析】（1）利用函数图像上的两个点的坐标列方程组，解方程组求得的值.‎ ‎（2）将原不等式分离常数，利用函数的单调性，求出的取值范围.‎ ‎【详解】‎ ‎（1）由于函数图像经过，，所以，解得，所以.‎ ‎（2）原不等式为，即在时恒成立，而在时单调递减，故在时有最小值为，故.所以实数的取值范围是.‎ ‎【点睛】‎ 本小题主要考查待定系数法求函数的解析式，考查不等式恒成立问题的求解策略，考查函数的单调性以及最值，属于中档题.‎ ‎22．已知定义域为的函数是奇函数 ‎（1）求实数的值（2）判断并证明在上的单调性 ‎（3）若对任意实数,不等式恒成立,求的取值范围 ‎【答案】（1）（2）见解析（3）‎ ‎【解析】（1）由是上的奇函数，得，且，代入可得的值；（2）由的解析式，用单调性定义可以证明是定义域上的减函数；（3）对任意实数，不等式恒成立，结合奇函数可得对恒成立，即可求得的取值范围.‎ ‎【详解】‎ ‎（1）由于定义域为的函数是奇函数,‎ ‎∴‎ ‎∴经检验成立 ‎（2）在上是减函数.‎ 证明如下:设任意 ‎∵∴‎ ‎∴在上是减函数 ,‎ ‎（3）不等式,‎ 由奇函数得到所以,‎ 由在上是减函数,∴对恒成立 ‎∴或 综上:.‎ ‎【点睛】‎ 本题考查了函数的奇偶性与单调性的性质和应用，以及不等式恒成立问题.解函数不等式：首先根据函数的性质把不等式转化为的形式，然后根据函数的单调性去掉“”，转化为具体的不等式(组)，此时要注意与的取值应在外层函数的定义域内.‎