2019-2020高考真题分类汇编 专题八 立体几何 第二十三讲 空间中点、直线、平面之间的位置关系答案

2019-2020高考真题分类汇编 专题八 立体几何 第二十三讲 空间中点、直线、平面之间的位置关系答案

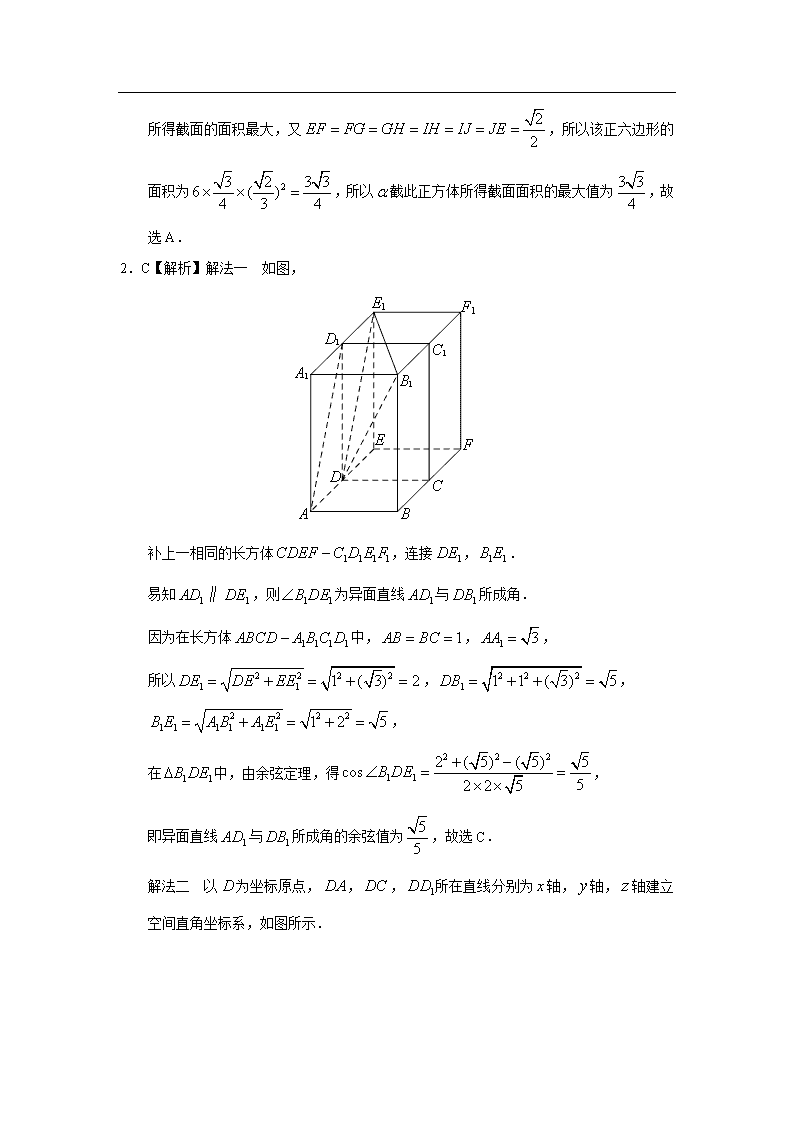
专题八 立体几何 第二十三讲 空间中点、直线、平面之间的位置关系 答案部分 ‎2019年 ‎1.解析 如图所示，联结，.‎ 因为点为正方形的中心，为正三角形，平面平面，是线段的中点，所以平面，平面，因为是中边上的中线，是中边上的中线，直线，是相交直线，设，则，，‎ 所以，， 所以．故选B．‎ ‎2.解析：对于A，内有无数条直线与平行，则与相交或，排除；‎ 对于B，内有两条相交直线与平行，则；‎ 对于C，，平行于同一条直线，则与相交或，排除；‎ 对于D，，垂直于同一平面，则与相交或，排除．‎ 故选B．‎ ‎3.证明：（1）因为D，E分别为BC，AC的中点，‎ 所以ED∥AB.‎ 在直三棱柱ABC-A1B1C1中，AB∥A1B1，[来源:学.科.网Z.X.X.K]‎ 所以A1B1∥ED.[来源:学科网]‎ 又因为ED⊂平面DEC1，A1B1平面DEC1，‎ 所以A1B1∥平面DEC1.‎ ‎（2）因为AB=BC，E为AC的中点，所以BE⊥AC.‎ 因为三棱柱ABC-A1B1C1是直棱柱，所以CC1⊥平面ABC.‎ 又因为BE⊂平面ABC，所以CC1⊥BE.‎ 因为C1C⊂平面A1ACC1，AC⊂平面A1ACC1，C1C∩AC=C，‎ 所以BE⊥平面A1ACC1.‎ 因为C1E⊂平面A1ACC1，所以BE⊥C1E.‎ ‎4.解析：由l，m是平面α外的两条不同直线，知：  由线面平行的判定定理得： 若，则．‎ 由线面平行、垂直的性质定理得，则.‎ ‎2010-2018年 ‎1．A【解析】记该正方体为，正方体的每条棱所在直线与平面所成的角都相等，即共点的三条棱，，与平面所成的角都相等，如图，‎ 连接，，，因为三棱锥是正三棱锥，所以，，与平面所成的角都相等，分别取，，，，，的中点，，，，，，连接，．，，，，易得，，，，，六点共面，平面与平面 平行，且截正方体所得截面的面积最大，又，所以该正六边形的面积为，所以截此正方体所得截面面积的最大值为，故选A．‎ ‎2．C【解析】解法一 如图，‎ ‎[来源:学科网ZXXK]‎ 补上一相同的长方体，连接，．‎ 易知，则为异面直线与所成角．‎ 因为在长方体中，，，‎ 所以，，‎ ‎，‎ 在中，由余弦定理，得，‎ 即异面直线与所成角的余弦值为，故选C．‎ 解法二 以为坐标原点，，，所在直线分别为轴，轴，轴建立空间直角坐标系，如图所示．‎ 由条件可知，，，，‎ 所以，，‎ 则由向量夹角公式，得，‎ 即异面直线与所成角的余弦值为，故选C．‎ ‎3．A【解析】若，，∥，由线面平行的判定定理知∥．若∥，，，不一定推出∥，直线与可能异面，故“∥”是“∥”的充分不必要条件．故选A．‎ ‎4．D【解析】由题意知四棱锥为正四棱锥，如图，‎ 连接，记，连接，则平面，取的中点，连接，，，易得，则，，易知．‎ 因为∥，，，所以也为与平面所成的角，即与平面所成的角，再根据最小角定理知，，所以，故选D．‎ ‎5．C【解析】如图所示，把三棱柱补成四棱柱，异面直线与所成角为 ‎,‎ ‎，，‎ ‎∴．选C．‎ ‎6．B【解析】设为三角形中心，底面如图2，过作，，，由题意可知，，，‎ 图1 图2‎ 由图2所示，以为原点建立直角坐标系，不妨设，则，，，，∵，，∴，，则直线的方程为，直线的方程为，直线 的方程为，根据点到直线的距离公式，知，，，∴，，‎ 因为，，为锐角，所以．选B ‎7．A【解析】因为过点的平面与平面平行，平面∥平面，所以∥∥，又∥平面，所以∥，则与所成的角为所求角，所以，所成角的正弦值为，选A．‎ ‎8．B【解析】由“且”推出“或”，但由“且”可推出“”，所以“”是“”的必要而不充分条件，故选B．‎ ‎9．B【解析】解法一 设，，则由题意知．‎ 在空间图形中，连结，设=．‎ 在中，．‎ 过作，过作，垂足分别为．‎ 过作，使四边形为平行四边形，则，‎ 连结，则就是二面角的平面角，所以．‎ 在中，，．‎ 同理，，，故．‎ 显然平面，故．‎ 在中，．‎ 在中，‎ ‎=‎ ‎，‎ 所以 ‎，‎ 所以（当时取等号），‎ 因为，，而在上为递减函数，‎ 所以，故选B．‎ 解法二 若，则当时，，排除D；‎ 当时，，，排除A、C，故选B．‎ ‎10．D【解析】利用正方体模型可以看出，与的位置关系不确定．选D．‎ ‎11．C【解析】选项中均可能与平面平行、垂直、斜交或在平面内，故选．‎ ‎12．B【解析】对于选项A，若，则与可能相交、平行或异面，A错误；显然选项B正确；对于选项C，若，，则或，C错误；对于选项D，若，，则或或与相交，D错误．故选B．‎ ‎13．D【解析】作，垂足为，设，则，由余弦定理，‎ ‎，‎ 故当时，取得最大值，最大值为．‎ ‎14．B【解析】直线与平面所成的角为的取值范围是 ‎，由于，‎ ‎， ‎ 所以的取值范围是．‎ ‎15．D【解析】作正方形模型，为后平面，为左侧面 ‎ 可知D正确．‎ ‎16．D【解析】A中可能平行、垂直、也可能为异面；B中还可能为异面；C中 应与中两条相交直线垂直时结论才成立，选D．‎ ‎17．B【解析】利用排除法可得选项B是正确的，∵∥，⊥，则．如选项A：‎ ‎∥，∥时，⊥或∥；选项C：若⊥，⊥，∥或；‎ 选项D：若⊥, ⊥，∥或⊥．‎ ‎18．B【解析】过点作，若存在某个位置，使得，则面，从而有，计算可得与不垂直，则A不正确；当翻折到时，因为，所以面，从而可得；若，因为，所以面，从而可得，而，所以这样的位置不存在，故C不正确；同理，D也不正确，故选B．‎ ‎19．D【解析】对于D，若平面平面，则平面内的某些直线可能不垂直于平面，即与平面的关系还可以是斜交、平行或在平面内，其余选项易知均是正确的．‎ ‎20．D【解析】D 两平行直线的平行投影不一定重合，故A错；由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可知、均错误，故选D．‎ ‎21．【解析】如图所示，‎ 设在底面的射影为，连接，．的面积为 ‎，‎ ‎∴，．∵与底面所成的角为，∴，‎ ‎．‎ ‎∴底面周长，‎ ‎∴圆锥的侧面积为．‎ ‎22．②③④【解析】对于命题①，可运用长方体举反例证明其错误：‎ 如图，不妨设为直线，为 直线,所在的平面为．‎ 所在的平面为，显然这些 直线和平面满足题目条件，但不成立．‎ 命题②正确，证明如下：设过直线的某平面与平面相交于直线，则，‎ 由，有，从知结论正确．‎ 由平面与平面平行的定义知命题③正确．‎ 由平行的传递性及线面角的定义知命题④正确．‎ ‎23．【解析】如图连接，取的中点，连接，则．‎ 则异面直线，所成的角为，由题意可知，，‎ ‎∴．又，，，∴，‎ 则．‎ ‎24．【解析】为轴，为轴，为轴建立坐标系，‎ 设正方形边长为．‎ 令 ‎，即． ‎ ‎25．②③【解析】如图为底面圆的内接正方形，设，‎ 则，‎ 即侧面均为等边三角形，∵底面，‎ 假设，由题意，当直线与成60°角时，由图可知与成60°角，所以①错，②正确；假设，可知③正确，④错．所以正确为②③．‎ ‎26．【证明】(1)在平行六面体中，．‎ 因为平面，平面，‎ 所以∥平面．‎ ‎(2)在平行六面体中，四边形为平行四边形．‎ 又因为，所以四边形为菱形，‎ 因此⊥．‎ 又因为⊥，∥，‎ 所以⊥．‎ 又因为=，平面，平面，‎ 所以⊥平面．‎ 因为平面，‎ 所以平面⊥平面．‎ ‎27．【解析】(1)由，，，，得 ‎，‎ 所以．‎ 故．‎ 由，，，，得，‎ 由，得，‎ 由，得，所以，故．‎ 因此平面．‎ ‎(2)如图，过点作，交直线于点，连结．‎ 由平面得平面平面，‎ 由得平面，‎ 所以是与平面所成的角．‎ 由，，‎ 得，，‎ 所以，故．‎ 因此，直线与平面所成的角的正弦值是．‎ 方法二 (1)如图，以的中点为原点，分别以射线，为，轴的正半轴，建立空间直角坐标系．‎ 由题意知各点坐标如下：‎ ‎，，，，，‎ 因此，，，‎ 由得．‎ 由得．‎ 所以平面．‎ ‎(2)设直线与平面所成的角为．‎ 由(1)可知，，，‎ 设平面的法向量．‎ 由，即，可取．‎ 所以．‎ 因此，直线与平面所成的角的正弦值是．‎ ‎28．【解析】（Ⅰ）如图，设PA中点为F，连结EF，FB．‎ 因为E，F分别为PD，PA中点，所以EF∥AD且，‎ 又因为BC∥AD，，所以 EF∥BC且EF=BC，‎ 即四边形BCEF为平行四边形，所以CE∥BF，‎ 因此CE∥平面PAB．‎ ‎（Ⅱ）分别取BC，AD的中点为M，N．连结PN交EF于点Q，连结MQ．‎ 因为E，F，N分别是PD，PA，AD的中点，所以Q为EF中点，‎ 在平行四边形BCEF中，MQ∥CE．‎ 由为等腰直角三角形得 PN⊥AD．‎ 由DC⊥AD，N是AD的中点得 BN⊥AD．‎ 所以AD⊥平面PBN，‎ 由BC∥AD得BC⊥平面PBN，‎ 那么，平面PBC⊥平面PBN．‎ 过点Q作PB的垂线，垂足为H，连结MH．‎ MH是MQ在平面PBC上的射影，所以∠QMH是直线CE与平面PBC所成的角．‎ 设CD=1．‎ 在中，由PC=2，CD=1，PD=得CE=，‎ 在△PBN中，由PN=BN=1，PB=得，‎ 在中，，MQ=，‎ 所以，‎ 所以，直线CE与平面PBC所成角的正弦值是．‎ ‎29．【解析】证明：（1）在平面内，因为，，所以．‎ 又因为平面，平面，所以∥平面．‎ ‎（2）因为平面⊥平面，‎ 平面平面=， ‎ 平面，，‎ 所以平面．‎ 因为平面，所以．‎ 又，，平面，平面，‎ 所以⊥平面，‎ 又因为平面，‎ 所以．‎ ‎30．【解析】（Ⅰ）因为，，‎ ‎，平面，，‎ 所以平面，‎ 又平面，‎ 所以，又，‎ 因此 ‎（Ⅱ）解法一：‎ 取的中点，连接，，．‎ 因为，‎ 所以四边形为菱形，‎ 所以．‎ 取中点，连接，，．‎ 则，，‎ 所以为所求二面角的平面角．‎ 又，所以．‎ 在中，由于，‎ 由余弦定理得，‎ 所以，因此为等边三角形，‎ 故所求的角为．‎ 解法二：‎ 以为坐标原点，分别以，，所在的直线为，，轴，建立如图所示的空间直角坐标系．‎ 由题意得，，，‎ 故，，，‎ 设是平面的一个法向量．‎ 由可得 取，可得平面的一个法向量．‎ 设是平面的一个法向量．‎ 由可得 取，可得平面的一个法向量．‎ 所以．‎ 因此所求的角为．‎ ‎31．【解析】（1）由正棱柱的定义，平面，‎ 所以平面平面，．‎ 记玻璃棒的另一端落在上点处．‎ 因为，．‎ 所以，从而．‎ 记与水平的交点为，过作，为垂足，‎ 则平面，故，‎ 从而．‎ 答：玻璃棒没入水中部分的长度为16cm．‎ ‎( 如果将“没入水中部分”理解为“水面以上部分”，则结果为24cm)‎ ‎ ‎ ‎（2）如图，，是正棱台的两底面中心．‎ 由正棱台的定义，⊥平面 ，‎ 所以平面⊥平面，⊥．‎ 同理，平面⊥平面，⊥．‎ 记玻璃棒的另一端落在上点处．‎ 过作⊥，为垂足， 则==32．[来源:学科网ZXXK]‎ 因为= 14，= 62，‎ 所以= ，从而．‎ 设则．‎ 因为，所以．‎ 在中，由正弦定理可得，解得．‎ 因为，所以．‎ 于是 ‎．‎ 记与水面的交点为，过作，为垂足，则 ⊥平面，故=12，从而 =．‎ 答:玻璃棒没入水中部分的长度为20cm．‎ ‎(如果将“没入水中部分”理解为“水面以上部分”，则结果为20cm)‎ ‎32．【解析】（Ⅰ）由已知可得，，所以平面．‎ 又平面，故平面平面．‎ ‎（Ⅱ）过作，垂足为，由（Ⅰ）知平面．‎ 以为坐标原点，的方向为轴正方向，为单位长度，建立如图所示的空间直角坐标系．‎ 由（Ⅰ）知为二面角的平面角，故，则，，可得，，，．‎ 由已知，，所以平面．‎ 又平面平面，故，．‎ 由，可得平面，所以为二面角的平面角，‎ ‎．从而可得．‎ 所以，，，．‎ 设是平面的法向量，则 ‎，即，‎ 所以可取．‎ 设是平面的法向量，则，‎ 同理可取．则．‎ 故二面角的余弦值为．‎ ‎33．【解析】（I）证明：∵，‎ ‎∴，∴．‎ ‎∵四边形为菱形，‎ ‎∴，∴，‎ ‎∴，∴．‎ ‎∵，∴；‎ 又，，∴，‎ ‎∴，∴，‎ ‎∴，∴．‎ 又∵，∴面．‎ ‎（Ⅱ）建立如图坐标系．‎ ‎，，，，‎ ‎，，，‎ 设面法向量，‎ 由得，取，∴．‎ 同理可得面的法向量，‎ ‎∴，∴．‎ ‎34．【解析】（Ⅰ）由已知得，‎ 取的中点，连接．‎ 由为中点知，． ‎ 又，故平行且等于，四边形为平行四边形，于是．‎ 因为平面，平面，所以平面．‎ ‎（Ⅱ）取的中点，连结，由得，从而，‎ 且．‎ 以为坐标原点，的方向为轴正方向，建立如图所示的空间直角坐标系，由题意知，‎ ‎，，，，‎ ‎，，‎ ‎．‎ 设为平面的法向量，则，即，‎ 可取，‎ 于是．‎ ‎35．【解析】（Ⅰ）设，连结OF，EC，‎ 由于E为AD的中点，，‎ 所以,‎ 因此四边形ABCE为菱形，所以O为AC的中点，又F为PC的中点，‎ 因此在中，可得．‎ 又平面，平面，所以∥平面．‎ ‎（Ⅱ）由题意知，，所以四边形为平行四边形，‎ 因此．又平面PCD，所以，因此．‎ 因为四边形ABCE为菱形，所以．‎ 又，AP，AC平面PAC，所以平面．‎ ‎36．【解析】（Ⅰ）∵为中点，∴DE∥PA ‎∵平面DEF，DE平面DEF，∴PA∥平面DEF ‎（Ⅱ）∵为中点，∴‎ ‎∵为中点，∴‎ ‎∴，∴，∴DE⊥EF ‎∵，∴‎ ‎∵，∴DE⊥平面ABC ‎∵DE平面BDE，∴平面BDE⊥平面ABC．‎ ‎37．【解析】（Ⅰ）连接BD交AC于点O，连结EO．‎ 因为ABCD为矩形，所以O为BD的中点．‎ 又E为PD的中点，所以EO∥PB．‎ EO平面AEC,PB平面AEC，所以PB∥平面AEC．‎ ‎（Ⅱ）因为PA平面ABCD，ABCD为矩形，所以AB，AD，AP两两垂直．‎ 如图，以A为坐标原点，的方向为x轴的正方向，为单位长，建立空间直角坐标系，‎ 则．‎ 设，则．‎ 设为平面ACE的法向量，‎ 则即，可取．[来源:Z§xx§k.Com]‎ 又为平面DAE的法向量，‎ 由题设，即，解得．‎ 因为E为PD的中点，所以三棱锥的高为．‎ 三棱锥的体积．‎ ‎38．【解析】（Ⅰ）证明：如图取PB中点M，连接MF，AM．因为F为PC中点，‎ 故MF//BC且MF=BC．由已知有BC//AD，BC=AD．又由于E为AD中点，‎ 因而MF//AE且MF=AE，故四边形AMFE为平行四边形，‎ 所以EF//AM，又AM平面PAB，而EF平面PAB，‎ 所以EF//平面PAB．‎ ‎（Ⅱ）（i）证明：连接PE，BE．因为PA=PD，BA=BD，而E为AD中点，‎ 故PEAD，BEAD，所以PEB为二面角P-AD-B的平面角．在三角形PAD中，‎ 由，可解得PE=2．‎ 在三角形ABD中，由，可解得BE=1．‎ 在三角形PEB中，PE=2，BE=1，，‎ 由余弦定理，可解得PB=，从而，即BEPB，‎ 又BC//AD，BEAD，从而BEBC，因此BE平面PBC．又BE平面ABCD，‎ 所以平面PBC平面ABCD．‎ ‎（ii）连接BF，由（i）知BE平面PBC．所以EFB为直线EF与平面PBC所成的角，‎ 由PB=，PA=，AB=得ABP为直角，而MB=PB=，可得AM=，‎ 故EF=，又BE=1，故在直角三角形EBF中，‎ 所以直线EF与平面PBC所成角的正弦值为 ‎39．【解析】（Ⅰ）设点O为AC，BD的交点，‎ 由AB＝BC，AD＝CD，得BD是线段AC的中垂线．‎ 所以O为AC的中点，BD⊥AC．‎ 又因为PA⊥平面ABCD，BD平面ABCD，‎ 所以PA⊥BD．所以BD⊥平面APC．‎ ‎（Ⅱ）连结OG．由(1)可知OD⊥平面APC，则DG在平面APC内的射影为OG，所以∠OGD是DG与平面APC所成的角．‎ 由题意得OG＝PA＝．‎ 在△ABC中，AC＝＝，‎ 所以OC＝AC＝．‎ 在直角△OCD中，OD＝＝2．‎ 在直角△OGD中，tan∠OGD＝．‎ 所以DG与平面APC所成的角的正切值为．‎ ‎（Ⅲ）连结OG．因为PC⊥平面BGD，OG平面BGD，所以PC⊥OG．‎ 在直角△PAC中，得PC＝．‎ 所以GC＝．‎ 从而PG＝，‎ 所以．‎ ‎40．【解析】（Ⅰ）由AB是圆O的直径，得AC⊥BC．‎ 由PA⊥平面ABC，BC平面ABC，得PA⊥BC，‎ 又PA∩AC=A,PA平面PAC，AC平面PAC，‎ 所以BC⊥平面PAC．‎ ‎（Ⅱ）连OG并延长交AC与M，链接QM，QO． ‎ 由G为∆AOC的重心，得M为AC中点，‎ 由G为PA中点，得QM//PC．‎ 又O为AB中点，得OM//BC．‎ 因为QM∩MO=M,QM平面QMO．‎ 所以QG//平面PBC．‎ ‎41．【解析】（Ⅰ）因为是直三棱柱，所以平面ABC,‎ 又平面,所以，又因为 平面，所以平面,‎ 又AD平面ADE,所以平面ADE平面．‎ ‎（Ⅱ）因为，为的中点，所以．因为平面，‎ 且平面，所以又因为，平面，‎ ‎，所以平面，所以AD．‎ 又AD平面，平面，所以平面．‎ ‎42．【解析】（Ⅰ）平面，面 又面 ‎（Ⅱ）是中点点到面的距离 三棱锥的体积 ‎（Ⅲ）取的中点为，连接，，‎ 又平面面面面，‎ 点是棱的中点，得：平面．‎ ‎43．【证明】：（Ⅰ）在△PAD中，因为E、F分别为AP，AD的中点，所以EF//PD．‎ 又因为EF平面PCD，PD平面PCD，所以直线EF//平面PCD．‎ ‎（Ⅱ）连结DB，因为AB=AD，∠BAD=60°，所以△‎ ABD为正三角形，因为F是AD的中点，所以BF⊥AD．因为平面PAD⊥平面ABCD，BF平面ABCD，平面PAD平面ABCD=AD，所以BF⊥平面PAD．又因为BF平面BEF，所以平面BEF⊥平面PAD．‎ ‎44．【解析】法一：（Ⅰ）证明：取AD中点G，连接PG，BG，BD．因PA=PD，‎ 有，在中，，有为等边 三角形，因此，‎ 所以平面PBG 又PB//EF，得，而DE//GB得AD DE，又，‎ 所以AD 平面DEF．‎ ‎（Ⅱ），为二面角P—AD—B的平面角，‎ 在 在 法二：（Ⅰ）取AD中点为G，因为 又为等边三角形，因此，，‎ 从而平面PBG．‎ 延长BG到O且使得PO OB，又平面PBG，PO AD，‎ 所以PO 平面ABCD．‎ 以O为坐标原点，菱形的边长为单位长度，直线OB，OP分别为轴，z轴，平行于AD的直线为轴，建立如图所示空间直角坐标系．‎ 设 由于 得 平面DEF．‎ ‎（Ⅱ）‎ 取平面ABD的法向量 设平面PAD的法向量 由 取 ‎45．【解析】（Ⅰ）因为四边形是正方形，所以//．故为异面直线与所成的角．因为平面，所以．故．‎ 在△中，=1，=，==3,‎ 故==．‎ 所以异面直线和所成角的余弦值为．‎ ‎（Ⅱ）证明：过点作//,交于点，则．由,可得,从而,又,=,所以平面．‎ ‎(Ⅲ)解：由（Ⅱ）及已知，可得=，即为的中点．取的中点，连接，则,因为//,所以//．过点作，交于，则为二面角--的平面角．‎ 连接，可得平面,故．从而．由已知，‎ 可得=．由//,,得．‎ 在△中，,‎ 所以二面角--的正切值为．‎ ‎46．【解析】 (Ⅰ)取的中点，连结，，由条件易知 ‎，．，．所以，．‎ 故四边形为平行四边形，所以 因为平面，平面，所以//平面 ‎（Ⅱ）在平行四边形中，设，则，‎ ‎，连，因为 在△中，可得=，‎ 在△中，可得=，‎ 在△中，因为，所以，‎ 在正三角形中，为中点，所以⊥．‎ 由平面⊥平面,‎ 可知⊥平面, ⊥．‎ 取的中点，连线、，‎ 所以⊥，⊥．‎ 因为交于，‎ 所以⊥平面，‎ 则∠为直线与平面所成角．‎ 在Rt△中，=, =，=，‎ 则cos=．‎ 所以直线与平面所成角的余弦值为．‎