- 2021-06-24 发布 |
- 37.5 KB |
- 45页


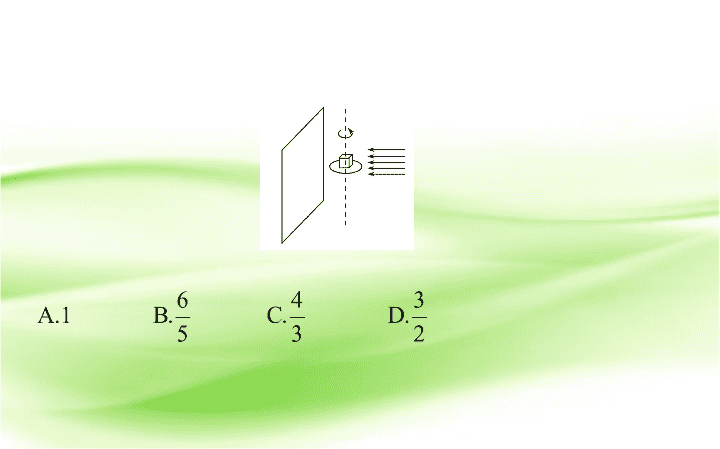
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届二轮复习选择填空题专练数学文化与核心素养课件(45张)(全国通用)
热点考向一 几何中的数学文化与核心素养 1. 如图所示 , 一个棱长为 1 的正方体在一个水平放置的转盘上转动 , 用垂直于竖直墙面的水平光线照射 , 该正方体在竖直墙面上的投影的面积记作 S, 则 S 的值不可能是 ( ) 【 解析 】 选 D. 由题意知 , 棱长为 1 的正方体在竖直墙面 上的投影面积 S 最小时为正方形 , 且边长为 1, 其面积为 1; 最大时为矩形 , 且相邻的两边长为 1 和 , 其面积为 1× 所以 S 的取值范围是 又因为 所以不可能的是选项 D. 2.(2018· 渭南二模 ) 祖暅原理 :“ 幂势既同 , 则积不容异”“幂”是截面积 ,“ 势”是几何体的高 , 意思是两个同高的几何体 , 如在等高处截面的面积恒相等 , 则体积相等 . 已知某不规则几何体与如图所示的几何体满足“幂势同” , 则该不规则几何体的体积为 世纪金榜导学号 ( ) 【 解析 】 选 A. 三棱锥的直观图如图所示 : 其中 SD⊥ 平面 ABC,BD⊥AC, 由三视图可知 AC=5, 所以三棱锥的体积为 由祖暅原理可知不规则几何体的体积为 热点考向二 数列中的数学文化与核心素养 1.(2018· 广州一模 ) 大衍数列 , 来源于 《 乾坤谱 》 中对 易传“大衍之数五十”的推论 , 主要用于解释中国传统 文化中的太极衍生原理 , 数列中的每一项 , 都代表太极 衍生过程中 , 曾经经历过的两仪数量总和 , 是中华传统 文化中隐藏着的世界数学史上第一道数列题 . 其规律是 : 偶数项是序号平方再除以 2, 奇数项是序号平方减 1 再除以 2, 其前 10 项依次是 0,2,4,8,12,18,24,32,40,50,…, 如图所示的程序框图是为了得到大衍数列的前 100 项而设计的 , 那么在两个“◇”中 , 可以先后填入 ( ) A.n 是偶数 ?,n≥100? B.n 是奇数 ?,n≥100? C.n 是偶数 ?,n>100? D.n 是奇数 ?,n>100? 【 解析 】 选 D.n=1,s=0, n=2,s=2, n=3,s=4, …, n=101>100, 结束循环 . 2.(2018· 开封一模 ) 我国古代名著 《 庄子 · 天下篇 》 中有一句名言“一尺之棰 , 日取其半 , 万世不竭” , 其意思为 : 一尺的木棍 , 每天截取一半 , 永远都截不完 . 现将该木棍依此规律截取 , 如图所示的程序框图的功能就是计算截取 7 天后所剩木棍的长度 ( 单位 : 尺 ), 则①②③处可分别填入的是 ( ) 【 解析 】 选 D. 由题意可得 : 由图可知第一次剩下 第 二次剩下 … 由此得出第 7 次剩下 可得①为 i≤7? ③i=i+1. 3. 中国有个名句“运筹帷幄之中 , 决胜千里之外” , 其 中的“筹”原意是指 《 孙子算经 》 中记载的算筹 . 古代 用算筹来进行计算 , 算筹是将几寸长的小竹棍摆在平面 上进行计算 , 算筹的摆放形式有横纵两种形式 ( 如图所 示 ), 表示一个多位数时 , 像阿拉伯计数一样 , 把各个数 位的数码从左到右排列 , 但各位数码的筹式需要纵横 相间 , 个位、百位、万位数用纵式表示 , 十位、千位、 十万位用横式表示 , 以此类推 . 例如 3 266 用算筹表示就 是 则 8 771 用算筹可表示为 ( ) 【 解析 】 选 C. 由算筹含义得到 8771 用算筹可表示为 热点考向三 函数与方程中的数学文化与核心 1. 地铁某换乘站设有编号为 A,B,C,D,E 的五个安全出口 . 若同时开放其中的两个安全出口 , 疏散 1 000 名乘客所需的时间如下表 , 则疏散乘客最快的一个安全出口的编号是 ( ) A.A B.B C.D D.E 安全出口编号 A,B B,C C,D D,E A,E 疏散乘客时间 (s) 120 220 160 140 200 【 解析 】 选 C. 同时开放 A,E 两个安全出口 , 疏散 1 000 名乘客所需的时间为 200 s, 同时开放 D,E 两个安全出口 , 疏散 1 000 名乘客所需的时间为 140 s, 得到 D 疏散乘客比 A 快 ; 同时开放 A,E 两个安全出口 , 疏散 1 000 名乘客所需的时间为 200 s, 同时开放 A,B 两个安全出口 , 疏散 1 000 名乘客所需的时间为 120 s, 得到 B 疏散乘客比 E 快 ; 同时开放 A,B 两个安全出口 , 疏散 1 000 名乘客所需的时间为 120 s, 同时开放 B,C 两个安全出口 , 疏散 1 000 名乘客所需的时间为 220 s, 得到 A 疏散乘客比 C 快 ; 同时开放 B,C 两个安全出口 , 疏散 1 000 名乘客所需的时间为 220 s, 同时开放 C,D 两个安全出口 , 疏散 1 000 名乘客所需的时间为 160 s, 得到 D 疏散乘客比 B 快 . 综上 , 疏散乘客最快的一个安全出口的编号是 D. 2. 某食品保鲜时间 y( 单位 : 小时 ) 与储藏温度 x( 单位 :℃) 满足函数关系 y=e kx+b (e=2.718… 为自然对数的底数 ,k,b 为常数 ). 若该食品在 0 ℃ 的保鲜时间是 192 小时 , 在 22 ℃ 的保鲜时间是 48 小时 , 则该食品在 33 ℃ 的保鲜时间是 ( ) A.16 小时 B.20 小时 C.24 小时 D.28 小时 【 解析 】 选 C.y=e kx+b (e=2.718… 为自然对数的底数 ,k,b 为常数 ). 当 x=0 时 ,e b =192, 当 x=22 时 e 22k+b =48, 所以 当 x=33 时 , 热点考向四 算术中的数学文化与核心素养 1.(2018· 洛阳二模 ) 数学家发现的“ 3x+1 猜想”是指 : 任取一个自然数 , 如果它是偶数 , 我们就把它除以 2, 如 果它是奇数 , 我们就把它乘以 3 再加上 1, 在这样一个变 换下 , 我们就得到一个新的自然数 , 如果反复使用这个 变换 , 我们就会得到一串自然数 , 猜想就是 : 反复进行 上述运算后 , 最后结果为 1, 现根据此猜想设计一个程序框图如图所示 , 执行该程序框图输入的 n=20, 则输出的结果为 ( ) A.6 B.7 C.8 D.9 【 解析 】 选 C. 由题意 , 模拟程序的运行 , 可得 n=20,i=1, 不满足条件 n 是奇数 ,n=10,i=2, 不满足条件 n=1, 执行循环体 , 不满足条件 n 是奇数 ,n=5, i=3, 不满足条件 n=1, 执行循环体 , 满足条件 n 是奇数 ,n=16, i=4, 不满足条件 n=1, 执行循环体 , 不满足条件 n 是奇数 ,n=8, i=5, 不满足条件 n=1, 执行循环体 , 不满足条件 n 是奇数 ,n=4, i=6, 不满足条件 n=1, 执行循环体 , 不满足条件 n 是奇数 ,n=2, i=7, 不满足条件 n=1, 执行循环体 , 不满足条件 n 是奇数 ,n=1, i=8, 满足条件 n=1, 退出循环 , 输出 i 的值为 8. 2. 辗转相除法是欧几里得算法的核心思想 , 如图所示的程序框图所描述的算法就是辗转相除法 , 若输入 m= 8 251,n=6 105, 则输出 m 的值为 ( ) 世纪金榜导学号 A.148 B.37 C.333 D.0 【 解析 】 选 B. 由程序框图知 : 程序的运行功能是求 m=8 251,n=6 105 的最大公约数 , 因为 8 251=6 105+2 146; 6 105=2×2 146+1 813; 2 146=1 813+333; 1 813=5×333+148; 333=2×148+37, 148=4×37+0 所以此时 m=37. 所以输出 m 的值是 37. 【 加练备选 】 1.(2018· 东北三省三校一模 ) 如图所示的程序框图的算法思路来源于我国古代数学名著 《 九章算术 》, 执行该程序框图若输出的 a=4, 则输入的 a,b 不可能为 ( ) A.4,8 B.4,4 C.12,16 D.15,18 【 解析 】 选 D. 根据题意 , 执行程序后输出的 a=4, 则执行该程序框图前 , 输入 a,b 的最大公约数是 4, 分析选项中的四组数 , 不满足条件的是选项 D. 2.(2018· 郑州一诊 )《 九章算术 》 是我国古代内容极 为丰富的数学名著 , 书中有如下问题 :“ 今有阳马 , 广五 尺 , 褒七尺 , 高八尺 , 问积几何 ?” 其意思为 :“ 今有底面 为矩形 , 一侧棱垂直于底面的四棱锥 , 它的底面长 , 宽分 别为 7 尺和 5 尺 , 高为 8 尺 , 问它的体积是多少 ?” 若以上 条件不变 , 则这个四棱锥的外接球的表面积为 ( ) A.128π 平方尺 B.138π 平方尺 C.140π 平方尺 D.142π 平方尺 【 解析 】 选 B. 因为今有底面为矩形 , 一侧棱垂直于底面的四棱锥 , 它的底面长、宽分别为 7 尺和 5 尺 , 高为 8 尺 , 所以构造一个长方体 , 其长、宽、高分别为 7 尺、 5 尺、 8 尺 , 则这个四棱锥的外接球就是这个长方体的外接球 , 所以这个四棱锥的外接球的半径 所以这个四棱锥的外接球的表面积为查看更多