- 2021-06-24 发布 |
- 37.5 KB |
- 45页

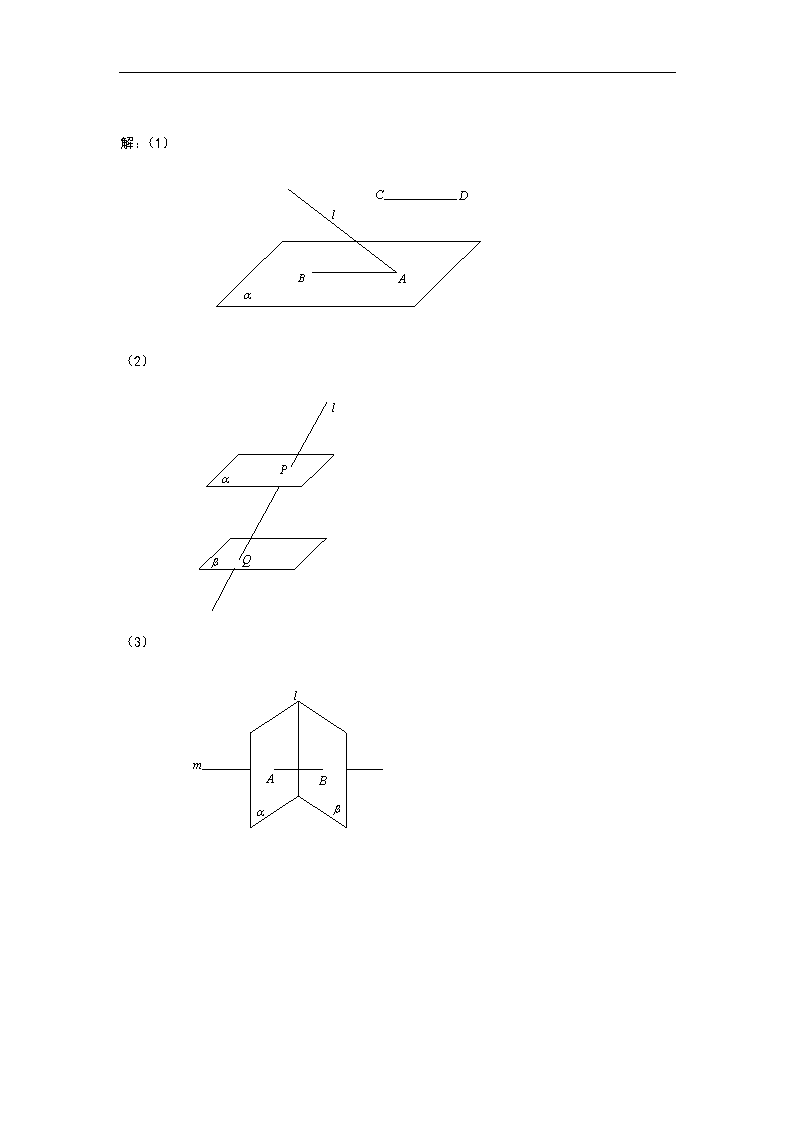
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中同步数学教案第14章 空间直线与平面
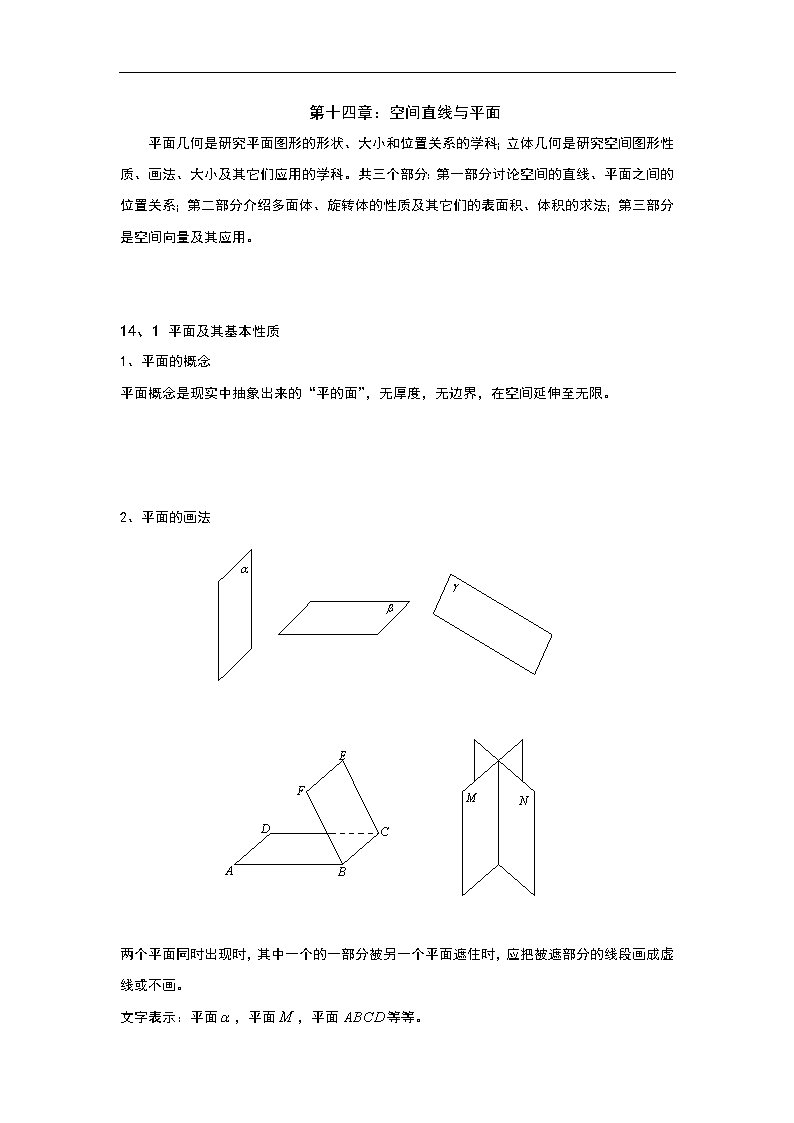
第十四章:空间直线与平面 平面几何是研究平面图形的形状、大小和位置关系的学科;立体几何是研究空间图形性质、画法、大小及其它们应用的学科。共三个部分:第一部分讨论空间的直线、平面之间的位置关系;第二部分介绍多面体、旋转体的性质及其它们的表面积、体积的求法;第三部分是空间向量及其应用。 14、1 平面及其基本性质 1、平面的概念 平面概念是现实中抽象出来的“平的面”,无厚度,无边界,在空间延伸至无限。 2、平面的画法 两个平面同时出现时,其中一个的一部分被另一个平面遮住时,应把被遮部分的线段画成虚线或不画。 文字表示:平面,平面,平面等等。 3、点、线、面及其位置关系的表示 点、、、…… 直线、、、……或直线、…… (点在直线上) (点不在直线上) (点在平面上) (点不在平面上) (直线在平面上,或说平面经过直线) (直线与平面相交于点) (直线与平面平行) (平面与平面相交于直线) (平面与平面平行) 例1、说出下列符号所表示的关系,并画出草图。 (1),,直线; (2)直线,直线,平面; (3)平面,直线,直线,,。 解:(1) (2) (3) 4、平面的基本性质 公理1:如果一条直线上有两点在一个平面内,那么这条直线上所有点都在这个平面内。(这时我们说:直线在平面内。或说:平面经过直线。) 集合语言表述:若,且,则。 公理1的作用:判断直线是否在平面内。 公理2:如果两个平面有一个公共点,那么它们有且只有一条经过这个公共点的公共直线。 集合语言表述:若,则,且 。 公理2的作用:判断两个平面相交的依据。 公理3:不在同一直线上的三点确定一个平面。 这里“确定一个平面”的含义是指“有且只有一个平面”。“有”指的是存在性,“只有”指的是唯一性。 公理3的作用:给出了确定平面的条件。 公理3的三个推论: 推论1:一条直线和直线外一点确定一个平面。 推论2:两条相交直线确定一个平面。 推论3:两条平行直线确定一个平面。 (推论证明略) 例2、下列命题是否正确,为什么? (1)两个平面有三个公共点,那么这两个平面重合。 (2)两个不重合的平面,如果有两个公共点,那么其他公共点都在直线上。 (3)四条边相等的四边形是菱形。 (4)梯形一定是平面图形。 (5)一个面内有无数条直线,这个面一定是平面。 解:(1)×;(2)√;(3)×;(4)√;(5)×。 例3、下列条件各能确定几个平面? (1)空间不在同一平面的四点。 (2)过同一点所作的三条直线。 (3)空间两两平行的四条直线。 (4)一条直线和直线外不共线的三个点。 解:(1)4个;(2)1个或3个;(3)1个,4个或6个;(4)1个,3个或4个。 例4、已知直线及平面,下列命题中: (1); (2); (3); (4)。 正确命题的序号为 。 解:(4) 例5、(1)一个平面把空间分成几个部分? (2)二个平面把空间分成几个部分? (3)三个平面把空间分成几个部分? 解:(1)2个;(2)3个或4个;(3)4个,6个,7个或8个。 例6、已知点直线,点,求证:直线共面。 例7、证明:如果一条直线与两条平行线都相交,那么这三条直线共面。 例8、已知直线,直线与直线分别交于,求证:直线共面。 证明:因为,所以确定一个平面(推论3),∵,∴,而,∴,即三直线共面,同理三线共面,又∵为相交直线,∴直线只能确定一个平面,所以直线所在平面与直线所在平面为同一平面,即直线共面。 例9、分别是正方体的棱的中点。求证:四点共面。 例10、在正方体中,若直线与平面交于点,求证:三点共线。 证明:连结,∵,∴确定平面, ∵,又∵,∴, 又∵,而,∴, 根据公理二,即三点共线。 例11、画出下图中,过三点的平面与其他平面的交线: 解:设,连结交于点,连结,则平面,平面。 例12、如图,已知,,求作直线与平面的交点。 解:∵,∴确定平面,又因为,所以,同理。在平面中与不平行,设它们交于点。 又∵,∴,所以为直线与平面的交点。 14、2 空间直线与直线的位置关系 1、空间两直线的位置关系 (1)平行——在同一个平面内,无公共点; (2)相交——在同一个平面内,有且只有一个公共点; (3)异面——不同在任何一个平面内,无公共点。 2、公理4:平行于同一条直线的两条直线互相平行 集合语言:若,,则 例1、在长方体的面内有一点,过点在面内作一条直线和平行,应该如何画,并说明理由。 画法:连结,过点在面内作一条直线,则即为所求直线。 证明:因为,又因为,所以为平行四边形,所以,根据公理4,。 3、定理1(等角定理):如果一个角的两边和另一个角的两边分别平行,那么这两个角相等或互补。 已知直线相交于点,直线相交于点,且,求证:所成的锐角(或直角)与所成的锐角(或直角)相等。 证明:在直线上分别取点,使,因为,所以在所确定的平面上过点作的平行线交于,∵位平行四边形,∴;在平行直线所确定的平面上过点作的平行线交于,同理可证。又∵和,∴,四边形为平行四边形,所以,,则,即。 例2、如图,在正方体中,,连结,求证:。 证明:在上取一点,使,连,∵,∴为平行四边形, ,又∵, ∴,为平行四边形,∴, ∵,∴,为平行四边形,所以,∴,同理,由等角定理,有。 练习: 如图,已知,且不在同一平面上,求证:。 4、异面直线的位置画法: 5、异面直线的证明通常用反证法。 6、异面直线所成角 设是两条异面直线,经过空间任意一点分别作直线,使得,则直线与所成的锐角(或直角)叫做异面直线所成角。 异面直线所成角范围是;两条直线所成角范围是,当两直线平行或重合时,所成角为0。若两条异面直线所成角为,我们就说这两条直线垂直。 例3、判断下列命题正确于否? (1)空间不相交的两条直线是异面直线; (2)分别在两个平面内的两条直线是异面直线; (3)某平面内一条直线及此平面外的一条直线是异面直线; (4)过异面直线外一点,必可作两条直线,使得。 解:(1)×;(2)×;(3)×;(4)√。 例4、在正方体中, (1)和棱异面的棱有哪几条? (2)和对角线成异面直线的棱有几条? (3)在12条棱中有几对异面直线? 解:(1),4条;(2)6条;(3)24对。 例5、已知直线与平面相交于点,直线,且,求证:直线和是异面直线。 证明:假设直线和不是异面直线,设和都在平面上,因为点与直线既在上,又在上,由推论1,与重合,所以直线在平面上,这与直线与平面相交矛盾,所以假设不成立,所以直线和是异面直线。 例6、已知直线与是异面直线,直线,且与不相交,求证:与为异面直线。 证明:假设与不是异面直线,则与共面,又∵与不相交,∴,而,由公理四有,这与直线与是异面直线矛盾,所以假设不成立,即与为异面直线。 例7、在正方体中,分别为的中点,求异面直线和所成角大小。 证明:过作交于,则(或其补角)为和所成的角,连结,设正方体的棱长为,则,,在中,由余弦定理有,所以和所成角为。 例8、在长方体中,,求异面直线和所成角的大小。 证明:延长至点,使,连结,所以(或其补角)是和所成的角。因为,所以为平行四边形,,在中,由余弦定理有,所以异面直线和所成角为。 例9、在空间四边形中,,是的中点,是的中点. (1)求异面直线与所成角的大小; (2)求异面直线与所成角的大小。 证明:(1)取中点,连结,则,所以(或其补角)是异面直线与所成角,在中,,由余弦定理有:,所以异面直线与所成角为。 (2)。 14、3 空间直线与平面的位置关系 1、空间直线与平面的位置关系: (1)直线在平面内——无数个公共点。 (2)直线与平面相交——一个公共点 (3)直线与平面平行——没有公共点 2、直线与平面垂直的定义:如果一条直线和一个平面内的所有直线都垂直,那么这条直线与这个平面垂直。 若直线与平面互相垂直,则记为,直线叫做平面的垂线,与平面的交点叫做垂足。 3、直线与平面垂直的判定: 定理2:如果直线与平面上的两条相交直线都垂直,那么直线与平面垂直。 (证明不作要求) 4、空间图形中的有关距离: (1)点到直线的距离:从直线外一点,引直线的垂线,该点与垂足间的距离叫做点到直线距离; (2)点到平面的距离:过平面外一点,引平面的垂线,该点与垂足间的距离叫做点到平面的距离; (3)直线到平面的距离:若一条直线平行于一个平面,在直线上任取一点,把该点到平面的距离叫做该直线到这个平面的距离; (4)平面到平面的距离:若两个平面互相平行,在其中一个平面上任取一点,把该点到另一个平面的距离叫做这两个平面间的距离; (5)异面直线距离:与两条异面直线都垂直相交的直线叫做这两条异面直线的公垂线,异面直线的公垂线在两条异面直线上的垂足间的距离叫做这两条异面直线间的距离。 例1、判断下列命题是否正确: (1)一条直线与平面内无数条直线都垂直,这条直线就垂直于这个平面。 (2)一条直线垂直于一个平面,它就与这个平面内任意一条直线垂直。 (3)一条直线不垂直于一个平面,那么它与这个平面内的所有直线都不垂直。 (4)一条直线与平面内的某条直线不垂直,那么不垂直于。 解:(1)×;(2)√;(3)×;(4)√。 例2、求证:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面。 已知直线,直线,求证:直线。 证明:在平面任意取一条直线,因为直线,由线面垂直的定义知道,又因为,所以,由的任意性及线面垂直的定义得到。 例3、在正方体,求证:。 证明:因为,所以, 又因为,所以,而, 所以,又因为,所以。 例4、已知,,垂足分别为,求证:。 证明:因为,所以,同理,所以,又因为,所以。 例5、已知长方体的棱的长分别为3,4,5。 (1)求点和点的距离; (2)求点到棱的距离; (3)求棱和平面的距离; (4)求异面直线和的距离。 解:(1);(2)5;(3)3;(4)3。 例6、在棱长为1的正方体中, (1)求点到直线的距离; (2)求直线和平面的距离; (3)求异面直线和的距离; (4)求异面直线和的距离 解:(1)连结,∵,∴, 又∵,∴,过作于,为斜边上的高,所以点到直线的距离为。 (2)过作于,∵,∴, 又∵,∴,所以,直线和平面的距离为。 (3)过作于,仿(2)可以证明,所以为异面直线和的公垂线段,异面直线和的距离为。 (4) 例7、在中,两直角边的长分别为9,12,平面,,求到斜边的距离。 解:过作于,连,∵,∴,所以,即为到斜边的距离。又因为,所以,即到斜边的距离为。 例8、已知边长为5,对角线长为8的菱形,它的两条对角线交于点,沿将面折起,使之成为空间四边形,求: (1)点到平面的距离; (2)当时,求点到平面的距离。 解:(1)∵,∴,为点到平面的距离,又因为,所以点到平面的距离为3。 (2)当时,为边长为4的正三角形,过作于,因为,所以,因而,就是点到平面的距离,而,所以点到平面的距离为。 5、斜线 一条直线和一个平面相交,但不和这个平面垂直,称这条直线和这个平面斜交。 和平面斜交的直线叫做这个平面的斜线。斜线与平面的交点叫做斜足。 6、直线和平面所成角 如图,直线是平面的一条斜线,斜足为,斜线上一点在平面上的射影为,则直线是斜线在平面上的射影。平面的斜线与它在平面内的射影所成的锐角,叫这条直线与这个平面所成的角。由定义可知:斜线与平面所成角的范围为。 规定:直线与平面垂直时,它们的所成角为;直线与平面平行(或直线在平面内)时,它们的所成角为0。 这样,直线与平面所成角的范围为。 例9、正方体的棱长为。 (1)求直线与平面所成角的大小; (2)求直线与平面所成角的大小; (3)若为棱的中点,求与平面所成角的大小; (4)求直线与平面所成角的大小。 解:(1)∵,∴,为在平面上的射影,所以为直线与平面所成角,等于。 (2)由(1),所以是在平面平面上的射影,所以为直线与平面所成角,又因为,所以,即直线与平面所成角。 (3)过作于,仿(1)可证,所以,所以,就是在平面上的射影,为与平面所成角,。 (4)过作于,连结,仿(1)可证,所以,所以,就是直线在平面上的射影,所以为直线与平面所成角,。 例10、在中,,为中点,平面,若与平面所成角分别为,求与平面所成角的大小。 解:因为,所以,设,则,又因为,所以,为中点,,所以,在中,,又因为,在平面上射影为,就是与平面所成角,,所以。 练习: 1.已知长方体中,,求: (1)与平面所成角的大小; (2)与平面所成角的大小; (3)与平面所成角的大小。 解:(1);(2);(3)。 2.直角梯形中,,,且。求: (1)和所成角的大小; (2)和平面所成角的大小。 解:和所成角分别为;和平面所成角为。 7、直线与平面平行的判定: 定理3:如果平面外一条直线和这个平面内一条直线平行,那么这条直线就和这个平面平行。 已知直线在平面外,直线,,求证:。 证明:假设直线不平行于平面,∵在平面外,∴,又∵,由推论三可以确定一个平面,∵,∴,由有,所以,所以,这与矛盾,所以假设不成立,所以。 8、直线与平面平行的性质: 定理4:如果一条直线和一个平面平行,经过这条直线的平面与这个平面相交,那么这条直线就和交线平行。 已知直线,,平面,求证:。 证明:假设直线与不平行,∵,∴与必相交,设交点为,∵,∴,所以直线与平面有公共点,这与矛盾,所以假设不成立,所以。 例11、判断下列命题是否正确: (1)已知两条直线,则必平行于过的一切平面。 (2)过平面外一点有且只有一条直线平行于该平面。 (3)直线与平面不相交,则。 (4)平行于同一平面的两条直线平行。 (5)已知直线平行于平面,那么直线平行于平面内的所有直线。 (6)两条平行线中的一条平行于一个平面,则另一条也平行于这个平面。 解:(1)×;(2)×;(3)×;(4)×;(5)×;(6)×。 例12、在正方体中,求证:直线。 证明:因为,所以, 又因为,所以,所以为平行四边形,所以,又因为,而在平面外,所以。 例13、在空间四边形中,分别是的中点,求证:。 证明:因为是的中点,所以,又因为,所以,同理。 例14、空间四边形ABCD中,分别是在AB、BC、CD上,且满足,,过的平面交于,连接。 (1)求; (2)求证:三线共点。 例15、已知平面,,,且,求证:且。 证明:∵不在平面,而,,∴,又因为,,所以,而,所以,即互相平行。 14、4 空间的平面与平面的位置关系 1、两个平面的位置关系: (1)两平面相交――有一条公共直线; (2)两平面平行――两个平面没有公共点。 2、二面角的定义:一条直线和由这条直线出发的两个半平面所组成的图形叫做二面角。这条直线叫做二面角的棱,这两个半平面叫做二面角的面。 二面角的画法如上图所示,分别记为,及。 3、二面角的平面角: 以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。 二面角的大小用它的平面角来度量,根据二面角的平面角的定义,二面角的范围为。 4、二面角大小的求法: 解决二面角问题关键是确定二面角的平面角位置,并通过计算求出二面角平面角的大小。 例1.已知正方体。 (1)求二面角的大小; (2)若为的中点,求二面角的大小。 证明:(1)取中点,连,∵都是等腰三角形,∴,是二面角的一个平面角,设正方体棱长为,则,∵, ∴为,所以,即二面角为。 (2)连,∵为等腰三角形,∴,为二面角的平面角,在中,,,所以,即二面角为。 例2.已知为正方形所在平面外一点,,,求: (1)二面角的大小; (2)二面角的大小; (3)二面角的大小; (4)二面角的大小; (5)二面角的大小; (6)二面角的大小。 解:(1);(2);(3);(4); (5)取中点,连结,∵都是等腰三角形, ∴,为二面角的平面角,又∵, ∴,即二面角为。 (6)过作于,连结,由对称性,所以为二面角的平面角,,在中,由余弦定理,所以,即二面角为。 例3.在二面角的棱上一点,在平面内作射线,在平面内作射线,已知,,求二面角的大小。 解:设,过点在平面作交于,在平面内作交于,连结,由作法知道为二面角的平面角。因为,所以,,又因为,所以,在中,所以,即二面角为。 例4.一个斜坡和水平面成的二面角,沿斜坡内一条与坡脚成的直路前进了100米,问升高了多少米? 已知,二面角为,求点到平面的距离。 解:过作于,所以为点到平面的距离。过作于,连结,因为,所以,又因为,所以,所以,为二面角的平面角,,,所以点到平面的距离为。 5、两个平面平行的判定: 定理5:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行。 已知直线平面,直线平面,,且,求证:。 证明:用反证法。假设平面与平面不平行,则设,因为,同理, 所以,与矛盾,所以假设不成立,所以。 6、两个平面平行的性质: 定理6:如果两个平行平面同时和第三个平面相交,那么它们的交线互相平行。 已知平面,求证:。 证明:假设直线与不平行,因为,所以相交,设,因为, ,所以,同理,所以,这与矛盾,所以假设不成立,所以。 例5、判断下列说法是否正确: (1)如果一个平面内有无数条直线平行于另一个平面,那么这两个平面平行。 (2)如果一个平面内任意一条直线都平行于另一个平面,则这两个平面平行。 (3)两个平面平行,则一个平面内的直线与另一个平面内的直线都平行。 (4)两个平面平行,则一个平面内的任意一条直线都平行于另一个平面。 (5)平行于同一直线的两个平面互相平行。 (6)是异面直线,则必存在经过直线的一个平面,与直线平行。 解:(1)×;(2)√;(3)×;(4)√;(5)×;(6)√。 例6、在长方体中,求证: (1)平面; (2)平面。 证明:(1)∵,∴,同理, 又∵,,所以。 (2)∵,,∴为平行四边形,, 所以,同理,又因为,,所以。 例7、求证:夹在两个平行平面间的平行线段的长相等。 已知平面,,且,求证:。 证明:因为,所以确定一个平面,且,因为,所以,所以为平行四边形,所以。 例8、有两个全等的正方形和不共面,对角线和上各有一点和,且,连,求证:。 证明(一):过作交于,过作交于,连,则,且,因为,所以,所以,为平行四边形,所以,而,在平面外,所以。 证明(二):连结延长交直线于点,连结,∵, 又∵,∴,∴,而,在平面外,所以。 证明(三):在平面内过作交于,连结,∵, ∴。所以,又因为,所以,,所以。查看更多