高中数学：《平行线分线段成比例》课件1（新人教A版选修4-1）

高中数学：《平行线分线段成比例》课件1（新人教A版选修4-1）

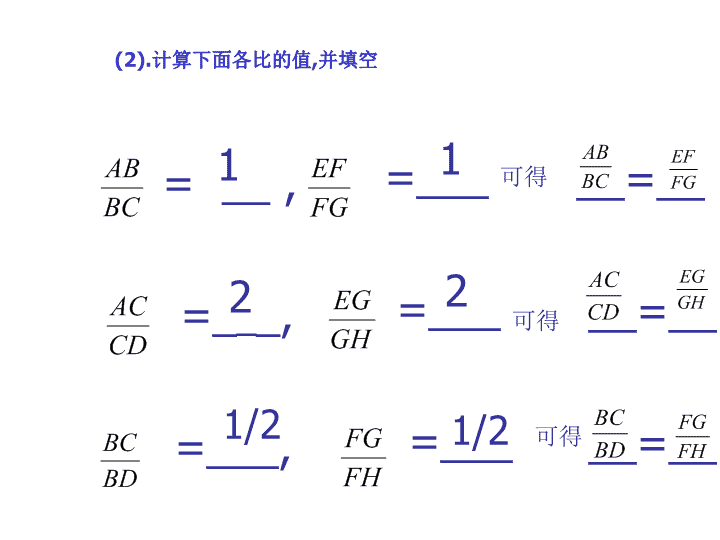
平行线分线段成比例定理 一、复习提问 1、说出平行线等分线段定理 2、观察图（1）已知 L1∥L2 ∥ L3 ∥ L4 ，AB=BC=CD (1)你能推出怎样的结论？ L4 L1 L2 L3 A B C D E F G H （1） ∵ L1∥L2 ∥ L3 ∥ L4 AB=BC=CD ∴ EF=FG=GH (2). 计算下面各比的值,并填空 = __ , =___ 可得 __=__ =_ _ _, =___ 可得 __=__ =___, =___ 可得 __=__ 1 1 2 2 1/2 1/2 二、新知识： 平行线分线段成比例定理 问题1 ：若将图（1）中的直线 L3 擦掉得到图（2），仍 使 L1∥L2 ∥ L4 不变，你能否发现在两直线 a，b 上截得 的线段有什么关系？ L4 L1 L2 A B D E F H （2） a b 通过计算可以得到： 由此可得到 ： 1、 平行线分线段成比例定理 ： 三条平行线截两条直线所 得的 对应线段 成比例。 说明 ： ①定理的条件是 “ 三条平行线截两条直线 ” ②是 “ 对应线段成比例 ” ，注意 “ 对应 ” 两字。 强化 “对应“ 两字理解和记忆如图（2） 练一练 ：如图（3） L1∥L2 ∥ L3 ， 试根据图形写出 成比例线段。 L3 (3) a b L1 L2 A B C D E F L4 L1 L2 A B D E F H （2） a b 注 ： “ 对应线段 ” 是指一条直线 被两条平行线截得的线段与另 一条直线被这两条平行线截得 的线段成对应线段。而 “ 对应线 段成比例 ” 是指同一条直线上的 两条线段的比等于与他们 对应 的另一条直线上的两条线段的比 例题解析 ： 例1、   已知：如图 L1 ∥ L2 ∥ L3 ， AB=3 ， DE=2 ， EF=4， 求 BC L1 L2 L3 A B C D E F 分析 ：图形已具备什么定理的基本图形？ 平行线分线段成比例定理 那么如何求线段 BC 的长呢？ （建立比例） 解 ： ∵ L1 ∥ L2 ∥ L3 ∴ （平行线分线段成比例定理） 即 ∴ 2 BC=3×4 BC=6 例 2 ：已知：如图（5）， L1 ∥ L2 ∥ L3 ， 求证： L1 L2 L3 A B C D E F （图5） 分析 ：图形是平行线分线段成比例定理 的一个变式图形，由已知条件可以出现 由 ， 由比例性质发现 证明 ： ∵ L1 ∥ L2 ∥ L3 ∴ ( 平行线分线段成比例定理 ) ∴ 即 ∴ （三） 巩固练习 ： 1、课本 P21 3 ， 练习 1 、 2 2、如图（6） AB ∥ CD ∥ EF ， 则在图中下列关系式 一定成立的是（ ） A B C D E F （6） A、 B、 C、 D、 D 1、解： ∵ L1 ∥ L2 ∥ L3 ∴ （平行线分线段成比例定理） 即 ∴ DE = 2、证明 ： ∵ L1 ∥ L2 ∥ L3 ∴ （平行线分线段成比例定理） ∴ ∴ ∴ 返回 四、小结: 1、本节课介绍了平行线分线段成比例定理及应用； 2、在运用平行线分线段成比例定理时要注意弄清三条平行线截两条直线，所得哪条线段与哪条线段是对应线段，同时要根据需要写出正确的比例式 。 五、布置作业 课外作业： 如图7，已知 L1 ∥ L2 ∥ L3 ∥ L4， 求 X，Y 的值 3 5 4 3.5 x y L1 L2 L3 L4