- 2021-06-23 发布 |
- 37.5 KB |
- 21页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学卷·2018届宁夏育才中学学益校区高二下学期第一次月考数学试卷(文科) (解析版)
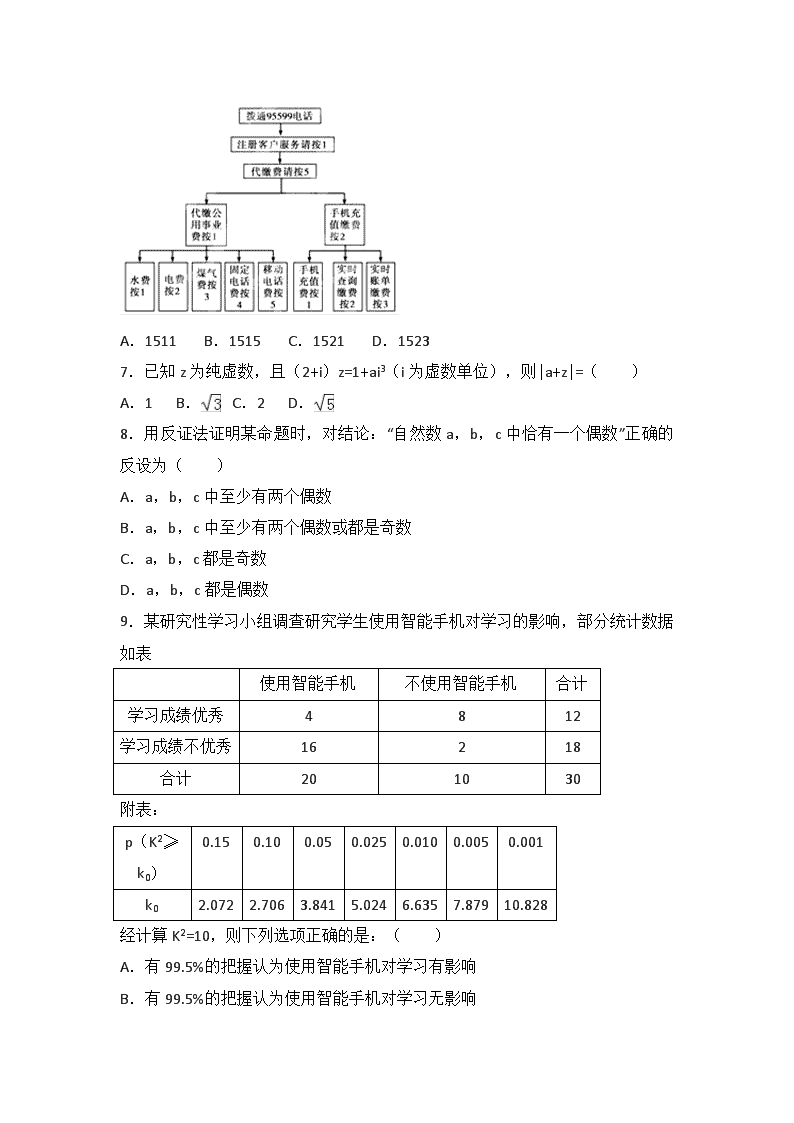
2016-2017学年宁夏育才中学学益校区高二(下)第一次月考数学试卷(文科) 一、选择题(共12小题,每题5分) 1.下面使用类比推理恰当的是( ) A.“若a•3=b•3,则a=b”类推出“若a•0=b•0,则a=b” B.“若(a+b)c=ac+bc”类推出“(a•b)c=ac•bc” C.“(a+b)c=ac+bc”类推出“=+(c≠0)” D.“(ab)n=anbn”类推出“(a+b)n=an+bn” 2.复数等于( ) A.16+16i B.﹣16﹣16i C.16﹣16i D.﹣16+16i 3.复平面上矩形ABCD的四个顶点中,A、B、C所对应的复数分别为2+3i、3+2i、﹣2﹣3i,则D点对应的复数是( ) A.﹣2+3i B.﹣3﹣2i C.2﹣3i D.3﹣2i 4.按流程图的程序计算,若开始输入的值为x=3,则输出的x的值是( ) A.6 B.21 C.156 D.231 5.下表为某班5位同学身高x(单位:cm)与体重y(单位kg)的数据,若两个量间的回归直线方程为,则a的值为( ) 身高 170 171 166 178 160 体重 75 80 70 85 65 A.﹣121.04 B.123.2 C.21 D.﹣45.12 6.如图所示,某人拨通了电话,准备手机充值须如下操作( ) A.1511 B.1515 C.1521 D.1523 7.已知z为纯虚数,且(2+i)z=1+ai3(i为虚数单位),则|a+z|=( ) A.1 B. C.2 D. 8.用反证法证明某命题时,对结论:“自然数a,b,c中恰有一个偶数”正确的反设为( ) A.a,b,c中至少有两个偶数 B.a,b,c中至少有两个偶数或都是奇数 C.a,b,c都是奇数 D.a,b,c都是偶数 9.某研究性学习小组调查研究学生使用智能手机对学习的影响,部分统计数据如表 使用智能手机 不使用智能手机 合计 学习成绩优秀 4 8 12 学习成绩不优秀 16 2 18 合计 20 10 30 附表: p(K2≥k0) 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k0 2.072 2.706 3.841 5.024 6.635 7.879 10.828 经计算K2=10,则下列选项正确的是:( ) A.有99.5%的把握认为使用智能手机对学习有影响 B.有99.5%的把握认为使用智能手机对学习无影响 C.有99.9%的把握认为使用智能手机对学习有影响 D.有99.9%的把握认为使用智能手机对学习无影响 10.欲将方程+=1所对应的图形变成方程x2+y2=1所对应的图形,需经过伸缩变换φ为( ) A. B. C. D. 11.在极坐标系中,若过点A(3,0)且与极轴垂直的直线交曲线ρ=4cosθ于A、B两点,则|AB|=( ) A. B.2 C. D. 12.若定义运算:;,例如2⊗3=3,则下列等式不能成立的是( ) A.a⊗b=b⊗a B.(a⊗b)⊗c=a⊗(b⊗c) C.(a⊗b)2=a2⊗b2 D.c•(a⊗b)=(c•a)⊗(c•b)(c>0) 二、填空题(共4题,每题5分) 13.在极坐标系中,直线ρsin(θ+)=2被圆ρ=3截得的弦长为 . 14.已知x,y∈R,i是虚数单位.若x+yi与互为共轭复数,则x+y= . 15.已知数列{an}的前n项和为Sn,且a1=1,Sn=n2an(n∈N*),可归纳猜想出Sn的表达式 . 16.执行如图所示的程序框图,输出的S值为 . 三、解答题 17.(10分)设a,b,c是△ABC的3边,S是△ABC的面积,求证:c2﹣a2﹣b2+4ab≥4S. 18.(12分)实数m为何值时,复数. (1)为实数; (2)为虚数; (3)为纯虚数; (4)对应点在第二象限. 19.(12分)在极坐标系中,已知曲线C:ρ=sin(θ﹣),P为曲线C上的动点,定点Q(1,). (Ⅰ)将曲线C的方程化成直角坐标方程,并说明它是什么曲线; (Ⅱ)求P、Q两点的最短距离. 20.(12分)已知B村位于A村的正西方1km处,原计划经过B村沿北偏东60°的方向设一条地下管线m,但在A村的西北方现400m处,发现一古代文物遗址w.根据初步侦探的结果,文物管理部门将遗址w周围100m范围划为禁区,试问埋设地下管线m的计划是否需要修改? 21.(12分)为了研究“教学方式”对教学质量的影响,某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).如图所示茎叶图为甲、乙两班某地随着经济的发展,居民收入逐年增长,如表是该地一建设银行连续五年的储蓄存款(年底余额),如下表: 年份x 2011 2012 2013 2014 2015 储蓄存款y(千亿元) 5 6 7 8 10 为了研究计算的方便,工作人员将上表的数据进行了处理,t=x﹣2010,z=y﹣5得到如下表: 时间代号t 1 2 3 4 5 z 0 1 2 3 5 (Ⅰ)求z关于t的线性回归方程; (Ⅱ)通过(Ⅰ)中的方程,求出y关于x的回归方程; (Ⅲ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少? (附:对于线性回归方程,其中:, =﹣) 2016-2017学年宁夏育才中学学益校区高二(下)第一次月考数学试卷(文科) 参考答案与试题解析 一、选择题(共12小题,每题5分) 1.下面使用类比推理恰当的是( ) A.“若a•3=b•3,则a=b”类推出“若a•0=b•0,则a=b” B.“若(a+b)c=ac+bc”类推出“(a•b)c=ac•bc” C.“(a+b)c=ac+bc”类推出“=+(c≠0)” D.“(ab)n=anbn”类推出“(a+b)n=an+bn” 【考点】归纳推理. 【分析】判断一个推理过程是否是类比推理关键是看他是否符合类比推理的定义,即是否是由特殊到与它类似的另一个特殊的推理过程.另外还要看这个推理过程是否符合实数的性质. 【解答】解:对于A:“若a•3=b•3,则a=b”类推出“若a•0=b•0,则a=b”是错误的,因为0乘任何数都等于0, 对于B:“若(a+b)c=ac+bc”类推出“(a•b)c=ac•bc”,类推的结果不符合乘法的运算性质,故错误, 对于C:将乘法类推除法,即由“(a+b)c=ac+bc”类推出“=+”是正确的, 对于D:“(ab)n=anbn”类推出“(a+b)n=an+bn”是错误的,如(1+1)2=12+12 故选C 【点评】归纳推理与类比推理不一定正确,我们在进行类比推理时,一定要注意对结论进行进一步的论证,如果要证明一个结论是正确的,要经过严密的论证,但要证明一个结论是错误的,只需要举出一个反例. 2.复数等于( ) A.16+16i B.﹣16﹣16i C.16﹣16i D.﹣16+16i 【考点】复数代数形式的乘除运算. 【分析】化简(1+i)2=1﹣1+2i=2i,(1+i)4=(2i)2=﹣4,(1+i)8=(﹣4)2=16,从而解得. 【解答】解:∵(1+i)2=1﹣1+2i=2i, ∴(1+i)4=(2i)2=﹣4, ∴(1+i)8=(﹣4)2=16, ∴==16i(1+i)=﹣16+16i, 故选D. 【点评】本题考查了复数的化简与运算. 3.复平面上矩形ABCD的四个顶点中,A、B、C所对应的复数分别为2+3i、3+2i、﹣2﹣3i,则D点对应的复数是( ) A.﹣2+3i B.﹣3﹣2i C.2﹣3i D.3﹣2i 【考点】复数的代数表示法及其几何意义. 【分析】根据复数的几何意义以及矩形的性质即可得到结论. 【解答】解:根据复数的几何意义可得A(2,3),B(3,2),C(﹣2,﹣3), 设D(x,y),, 即(x﹣2,y﹣3)=(﹣5,﹣5), 则,解得x=﹣3,y=﹣2, 即D点对应的复数是﹣3﹣2i, 故选:B. 【点评】本题主要考查复数的几何意义,利用矩形的对边平行且相等是解决本题的关键. 4.按流程图的程序计算,若开始输入的值为x=3,则输出的x的值是( ) A.6 B.21 C.156 D.231 【考点】程序框图. 【分析】根据程序可知,输入x,计算出的值,若≤100,然后再把作为x,输入,再计算的值,直到>100,再输出. 【解答】解:∵x=3, ∴=6, ∵6<100, ∴当x=6时, =21<100, ∴当x=21时, =231>100,停止循环 则最后输出的结果是 231, 故选D. 【点评】此题考查的知识点是代数式求值,解答本题的关键就是弄清楚题图给出的计算程序. 5.下表为某班5位同学身高x(单位:cm)与体重y(单位kg)的数据,若两个量间的回归直线方程为,则a的值为( ) 身高 170 171 166 178 160 体重 75 80 70 85 65 A.﹣121.04 B.123.2 C.21 D.﹣45.12 【考点】线性回归方程. 【分析】首先做出这组数据的横标和纵标的平均数,写出这组数据的样本中心点,根据所给的线性回归方程,把样本中心点代入求出字母系数的值. 【解答】解:∵ =169 =75, ∴这组数据的样本中心点是(169,75) ∵两个量间的回归直线方程为, ∴75=1.16×169+a ∴a=﹣121.04 故选A. 【点评】本题考查线性回归方程,是一个基础题,题目的运算量比较小,因为题目中给出了线性回归方程的系数,这样减轻了同学们的运算量,是一个好题. 6.如图所示,某人拨通了电话,准备手机充值须如下操作( ) A.1511 B.1515 C.1521 D.1523 【考点】流程图的作用. 【分析】根据已知的流程图,我们可以分析出准备手机充值须进行的操作,按先后顺序排列按键,可得答案. 【解答】解:准备手机充值须如下操作: ①注册客户服务1 ②代缴费用5 ③手机充值缴费2 ④手机充值费1 即1﹣5﹣2﹣1 故选C. 【点评】本题考查的知识点是流程图,其中读图分析出流程图每种操作的具体步骤是解答的关键. 7.已知z为纯虚数,且(2+i)z=1+ai3(i为虚数单位),则|a+z|=( ) A.1 B. C.2 D. 【考点】复数求模. 【分析】利用复数的运算法则、纯虚数的定义、模的计算公式即可得出. 【解答】解:∵(2+i)z=1+ai3=1﹣ai, ∴(2﹣i)(2+i)z=(2﹣i)(1﹣ai), ∴z=, ∵z为纯虚数, ∴=0,≠0, 解得a=2. ∴z=﹣i. ∴|a+z|=|2﹣i|=. 故选:D. 【点评】本题考查了复数的运算法则、纯虚数的定义、模的计算公式,考查了推理能力与计算能力,属于中档题. 8.用反证法证明某命题时,对结论:“自然数a,b,c中恰有一个偶数”正确的反设为( ) A.a,b,c中至少有两个偶数 B.a,b,c中至少有两个偶数或都是奇数 C.a,b,c都是奇数 D.a,b,c都是偶数 【考点】反证法与放缩法. 【分析】找出题中的题设,然后根据反证法的定义对其进行否定. 【解答】解:∵结论:“自然数a,b,c中恰有一个偶数” 可得题设为:a,b,c中恰有一个偶数 ∴反设的内容是 假设a,b,c中至少有两个偶数或都是奇数. 故选B. 【点评】此题考查了反证法的定义,反证法在数学中经常运用,当论题从正面不容易或不能得到证明时,就需要运用反证法,此即所谓“正难则反“. 9.某研究性学习小组调查研究学生使用智能手机对学习的影响,部分统计数据如表 使用智能手机 不使用智能手机 合计 学习成绩优秀 4 8 12 学习成绩不优秀 16 2 18 合计 20 10 30 附表: p(K2≥k0) 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k0 2.072 2.706 3.841 5.024 6.635 7.879 10.828 经计算K2=10,则下列选项正确的是:( ) A.有99.5%的把握认为使用智能手机对学习有影响 B.有99.5%的把握认为使用智能手机对学习无影响 C.有99.9%的把握认为使用智能手机对学习有影响 D.有99.9%的把握认为使用智能手机对学习无影响 【考点】独立性检验的应用. 【分析】根据观测值K2,对照数表,即可得出正确的结论. 【解答】解:因为7.879<K2=10<10.828, 对照数表知,有99.5%的把握认为使用智能手机对学习有影响. 故选:A. 【点评】本题考查了独立性检验的应用问题,是基础题目. 10.欲将方程+=1所对应的图形变成方程x2+y2=1所对应的图形,需经过伸缩变换φ为( ) A. B. C. D. 【考点】伸缩变换. 【分析】设伸缩变换φ为,代入,化简计算即可得到. 【解答】解:设伸缩变换φ为, 则, 代入 得, ∴ 故选:B 【点评】本题考查了伸缩变换,关键是对变换公式的理解与运用,是基础题. 11.在极坐标系中,若过点A(3,0)且与极轴垂直的直线交曲线ρ=4cosθ于A、B两点,则|AB|=( ) A. B.2 C. D. 【考点】简单曲线的极坐标方程. 【分析】过点A(3,0)且与极轴垂直的直线方程为:x=3.曲线ρ=4cosθ即ρ2=4ρcosθ,化为方程:(x﹣2)2+y2=4.可得圆心C(2,0),半径r=2.利用勾股定理与弦长公式即可得出. 【解答】解:过点A(3,0)且与极轴垂直的直线方程为:x=3. 曲线ρ=4cosθ即ρ2=4ρcosθ,化为方程:x2+y2=4x,配方为:(x﹣2)2+y2=4.可得圆心C(2,0),半径r=2. ∴|AB|=2=2. 故选:B. 【点评】本题考查了极坐标方程化为直角坐标方程、勾股定理与弦长公式,考查了推理能力与计算能力,属于基础题. 12.若定义运算:;,例如2⊗3=3,则下列等式不能成立的是( ) A.a⊗b=b⊗a B.(a⊗b)⊗c=a⊗(b⊗c) C.(a⊗b)2=a2⊗b2 D.c•(a⊗b)=(c•a)⊗(c•b)(c>0) 【考点】函数的概念及其构成要素. 【分析】利用题中的新定义知a⊗b表示a,b中的最大值,分别对各选项判断表示的值. 【解答】解:由题中的定义知a⊗b表示a,b中的最大值 a⊗b与b⊗a表示的都是a,b中的最大值 (a⊗b)⊗c与a⊗(b⊗c)表示的都是a,b,c中的最大值 c•(a⊗b)表示a,b的最大值与c的乘积;(c•a)⊗(c•b)表示c•a与c•b中最大值故c•(a⊗b)=(c•a)⊗(c•b) 故A、B、D都对 故选C 【点评】本题考查充分理解题中的定义,并利用定义解题.新定义在近几年的高考中是常考. 二、填空题(共4题,每题5分) 13.在极坐标系中,直线ρsin(θ+)=2被圆ρ=3截得的弦长为 . 【考点】简单曲线的极坐标方程. 【分析】求得直线方程及圆的方程,利用点到直线的距离公式求得弦心距d,根据勾股定理即可求得弦长. 【解答】解:直线ρsin(θ+)=2即ρcosθ+ρsinθ=2,化为直角坐标方程为 x+y﹣2=0, 圆ρ=3,即x2+y2=9,表示以原点为圆心、半径为3的圆, 弦心距d=,可得弦长为2=2=2, 直线ρsin(θ+)=2被圆ρ=3截得的弦长2, 故答案为:. 【点评】本题考查直线句圆的参数方程及极坐标方程,考查点到直线的距离公式,考查计算能力,属于中档题. 14.已知x,y∈R,i是虚数单位.若x+yi与互为共轭复数,则x+y= 3 . 【考点】复数代数形式的乘除运算. 【分析】利用复数代数形式的乘除运算化简,再由共轭复数的概念求得x,y值,则答案可求. 【解答】解:∵ =, 且x+yi与互为共轭复数,∴x=2,y=1. ∴x+y=3. 故答案为:3. 【点评】本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题. 15.已知数列{an}的前n项和为Sn,且a1=1,Sn=n2an(n∈N*),可归纳猜想出Sn的表达式 . 【考点】归纳推理. 【分析】利用条件分别求出S1,S2,S3,S4的值,寻找规律,得到表达式. 【解答】解:因为a1=1,Sn=n2an,所以S1=a1=1, 当n=2时,S2=a1+a2=4a2,解得, 当n=3时,S3=a1+a2+a3=9a3,解得, 所以,, 所以, 故答案为:. 【点评】本题主要考查归纳推理的应用,根据条件先求出前几项的和,然后根据规律得到表达式. 16.执行如图所示的程序框图,输出的S值为 ﹣6 . 【考点】循环结构. 【分析】根据题意,i、S的初始值分别为1,0.该程序的意图是:当i≤3时,用(﹣1)i•i2+S值代替S,直到i=4时输出S的值,由此不难得到本题的答案. 【解答】解:该程序从i=1开始,直到i=4结束输出S的值,循环体被执行了3次 ①i=1,满足i<4,由于i是奇数,用S﹣i2代替S,得S=﹣1,用i+ 1代替i,进入下一步; ②i=2,满足i<4,由于i是偶数,用S+i2代替S,得S=3,用i+1代替i,进入下一步; ③i=3,满足i<4,由于i是奇数,用S﹣i2代替S,得S=﹣6,用i+1代替i,进入下一步; ④i=4,不满足i<4,结束循环体,并输出最后一个S值 故答案为:﹣6 【点评】本题给出程序框图,要我们求出最后输出值,着重考查了算法语句的理解和循环结构等知识,属于基础题. 三、解答题 17.(10分)(2017春•西夏区月考)设a,b,c是△ABC的3边,S是△ABC的面积,求证:c2﹣a2﹣b2+4ab≥4S. 【考点】余弦定理. 【分析】利用余弦定理、“作差法”、三角形的面积计算公式即可得出. 【解答】证明:由余弦定理可得:a2+b2﹣c2=2abcosC, ∴c2﹣a2﹣b2+4ab﹣S=4ab﹣2abcosC﹣ =4ab(1﹣) ≥0, ∴c2﹣a2﹣b2+4ab≥4S. 【点评】本题考查了余弦定理、“作差法”、三角形的面积计算公式,考查了推理能力与计算能力,属于中档题. 18.(12分)(2012春•桥东区校级期中)实数m为何值时,复数. (1)为实数; (2)为虚数; (3)为纯虚数; (4)对应点在第二象限. 【考点】复数的基本概念;复数的代数表示法及其几何意义. 【分析】利用复数的运算法则和有关概念即可得出. 【解答】解:. (1)z为实数⇔m2+8m+15=0且m+5≠0,解得m=﹣3; (2)z为虚数 解得m≠﹣3且m≠﹣5; (3)z为纯虚数 解得m=2; (4)z对应的点在第二象限 解得m<﹣5或﹣3<m<2. 【点评】熟练掌握复数的运算和有关概念是解题的关键. 19.(12分)(2015秋•石家庄校级期末)在极坐标系中,已知曲线C:ρ=sin(θ﹣),P为曲线C上的动点,定点Q(1,). (Ⅰ)将曲线C的方程化成直角坐标方程,并说明它是什么曲线; (Ⅱ)求P、Q两点的最短距离. 【考点】简单曲线的极坐标方程. 【分析】(Ⅰ)运用两角差的正弦公式和极坐标与直角坐标的关系:x=ρcosθ,y=ρsinθ,x2+y2=ρ2,化简即可得到所求方程及轨迹; (Ⅱ)求得Q的直角坐标,以及Q到圆心的距离,由最小值d﹣r,即可得到所求值. 【解答】解:(Ⅰ)曲线C:ρ=sin(θ﹣)=2(sinθ﹣cosθ) =2sinθ﹣2cosθ, 即有ρ2=2ρsinθ﹣2ρcosθ, 由x=ρcosθ,y=ρsinθ,x2+y2=ρ2, 可得曲线C:x2+y2+2x﹣2y=0, 即为以(﹣1,1)为圆心,为半径的圆; (Ⅱ)Q(1,),即为Q(cos,sin), 即Q(,), Q到圆心的距离为d==, 即有PQ的最短距离为d﹣r=﹣. 【点评】本题考查极坐标和直角坐标的互化,点与圆的位置关系,注意运用两点的距离公式,考查运算能力,属于基础题. 20.(12分)(2017春•西夏区月考)已知B村位于A村的正西方1km处,原计划经过B村沿北偏东60°的方向设一条地下管线m,但在A村的西北方现400m处,发现一古代文物遗址w.根据初步侦探的结果,文物管理部门将遗址w周围100m范围划为禁区,试问埋设地下管线m的计划是否需要修改? 【考点】解三角形的实际应用. 【分析】利用正弦定理求出AC,再求出A到直线BC的距离,即可得出结论. 【解答】解:如图所示,△ABC中,AB=1km,∠CBA=30°,∠CAB=45°, ∴∠ACB=105°, 由正弦定理可得, ∴AC=>0.5, 又建立坐标系,可得直线BC的方程为y=x,A(1,0)到直线的距离为=0.5 ∴埋设地下管线m的计划不需要修改. 【点评】本题考查了正弦定理,考查点到直线的距离公式,考查学生的计算能力,属于中档题. 21.(12分)(2016•辽宁校级模拟)为了研究“教学方式”对教学质量的影响,某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).如图所示茎叶图为甲、乙两班(2016秋•高台县校级期末)某地随着经济的发展,居民收入逐年增长,如表是该地一建设银行连续五年的储蓄存款(年底余额),如下表: 年份x 2011 2012 2013 2014 2015 储蓄存款y(千亿元) 5 6 7 8 10 为了研究计算的方便,工作人员将上表的数据进行了处理,t=x﹣2010,z=y﹣5得到如下表: 时间代号t 1 2 3 4 5 z 0 1 2 3 5 (Ⅰ)求z关于t的线性回归方程; (Ⅱ)通过(Ⅰ)中的方程,求出y关于x的回归方程; (Ⅲ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少? (附:对于线性回归方程,其中:, =﹣) 【考点】线性回归方程. 【分析】 (I)由所给数据看出,做出平均数,利用最小二乘法做出b,a,写出线性回归方程. (II)t=x﹣2010,z=y﹣5,代入z=1.2t﹣1.4得到y关于x的回归方程; (Ⅲ)把所给的x的值代入线性回归方程,求出变化以后的预报值,得到结果. 【解答】解:(Ⅰ),,,,, ∴z=1.2t﹣1.4•…(6分) (Ⅱ)t=x﹣2010,z=y﹣5,代入z=1.2t﹣1.4得到:y﹣5=1.2(x﹣2010)﹣1.4, 即y=1.2x﹣2408.4•…(9分) (Ⅲ)x=2020,∴y=1.2×2020﹣2408.4=15.6, ∴预测到2020年年底,该地储蓄存款额可达15.6千亿元•…(12分) 【点评】本题考查回归分析的基本思想及其初步应用,考查回归方程的意义和求法,考查数据处理的基本方法和能力,考查利用统计思想解决实际问题的能力.查看更多