- 2021-06-23 发布 |
- 37.5 KB |
- 15页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学复习单元评估检测(九)
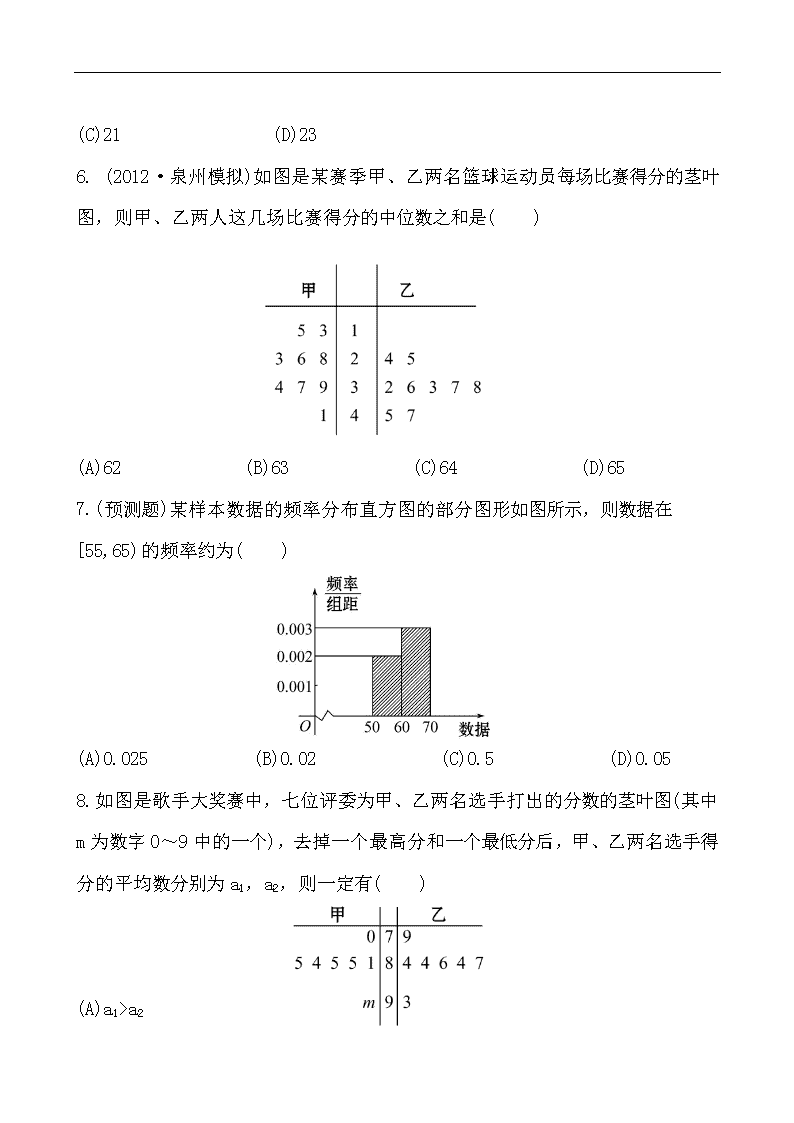
单元评估检测(九) (第九、十章) (120分钟 150分) 一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.(2012·福州模拟)如图是某次大赛中,7位评委 为某选手打出的分数的茎叶统计图,去掉一个最高 分和一个最低分后,所剩数据的平均数为( ) (A)83 (B)84 (C)85 (D)86 2.(2012·辽阳模拟)某单位员工按年龄分为A、B、C三个组,其人数之比为 5∶4∶1,现用分层抽样的方法从总体中抽取一个容量为20的样本,已知C组中甲、乙两人均被抽到的概率为则该单位员工总数为( ) (A)110 (B)100 (C)90 (D)80 3.有甲、乙两种钢材,从中各取等量样品检验它们的抗拉强度指标如下: 甲 X 110 120 125 130 135 P 0.1 0.2 0.4 0.1 0.2 乙 X 100 115 125 130 145 P 0.1 0.2 0.4 0.1 0.2 现要比较两种钢材哪一种抗拉强度较好,应检验哪项指标( ) (A)期望与方差 (B)正态分布 (C)K2 (D)概率 4.现要完成下列3项抽样调查: ①从10盒酸奶中抽取3盒进行食品卫生检查. ②科技报告厅有32排,每排有40个座位,有一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请32名听众进行座谈. ③高新中学共有160名教职工,其中一般教师120名,行政人员16名,后勤人员24名,为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本.较为合理的抽样方法是( ) (A)①简单随机抽样,②系统抽样,③分层抽样 (B)①简单随机抽样,②分层抽样,③系统抽样 (C)①系统抽样,②简单随机抽样,③分层抽样 (D)①分层抽样,②系统抽样,③简单随机抽样 5.(2012·杭州模拟)下面的程序语句输出的结果S为( ) (A)17 (B)19 (C)21 (D)23 6. (2012·泉州模拟)如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( ) (A)62 (B)63 (C)64 (D)65 7.(预测题)某样本数据的频率分布直方图的部分图形如图所示,则数据在[55,65)的频率约为( ) (A)0.025 (B)0.02 (C)0.5 (D)0.05 8. 如图是歌手大奖赛中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0~9中的一个),去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( ) (A)a1>a2 (B)a2>a1 (C)a1=a2 (D)a1、a2的大小不确定 9.已知程序框图如图所示,则该程序框图的功能是( ) (A)求数列的前10项和(n∈N*) (B)求数列的前10项和(n∈N*) (C)求数列的前11项和(n∈N*) (D)求数列的前11项和(n∈N*) 10.某市政府调查市民收入增减与旅游愿望的关系时,采用独立性检验法抽查了3 000人,计算发现K2=6.023,则根据这一数据查阅下表,市政府断言市民收入增减与旅游愿望有关系的可信程度是( ) P(K2≥k0) … 0.25 0.15 0.10 0.05 0.025 0.010 0.005 … k0 … 1.323 2.072 2.706 3.841 5.024 6.635 7.879 … (A)90% (B)95% (C)97.5% (D)99.5% 二、填空题(本大题共5小题,每小题4分,共20分.请把正确答案填在题中横线上) 11.如图,判断正整数x是奇数还是偶数,①处应填______. 12.如图所示的程序框图,若输入n=5,则输出的n值为_____. 13.某学院的A,B,C三个专业共有1 200名学生,为了调查这些学生勤工俭学的情况,拟采用分层抽样的方法抽取一个容量为120的样本.已知该学院的A专业有380名学生,B专业有420名学生,则在该学院的C专业应抽取______名学生. 14.(2012·厦门模拟)如图所示的是某班60 名同学参加2011年高中数学毕业会考所得 成绩(成绩均为整数)整理后画出的频率分布 直方图,根据图中可得出的该班不及格(60分 以下)的同学的人数为_____. 15.(2012·龙岩模拟)已知x、y的取值如下表所示: x 0 1 3 4 y 2.2 4.3 4.8 6.7 若y与x线性相关,且=0.95x+a,则a=_____. 三、解答题(本大题共6小题,共80分.解答时应写出必要的文字说明、证明过程或演算步骤) 16.(13分)(2012·唐山模拟)某校高三年级共有450名学生参加英语口语测试,其中男生250名,女生200名,现按性别用分层抽样的方法从中抽取45名学生的成绩. (1)求抽取的男生和女生的人数. (2)男生甲和女生乙至少有1人被抽到的概率. (3)从男生和女生中抽查的结果分别如下表1和表2: 表1: 成绩分组 (60,70] (70,80] (80,90] (90,100] 人数 3 m 8 6 表2: 成绩分组 (60,70] (70,80] (80,90] (90,100] 人数 2 5 n 5 分别估计男生和女生的平均分,并估计这450名学生的平均分.(精确到0.01) 17.(13分)给出算法: 第一步:输入大于2的整数n. 第二步:依次检验从2到n-1的整数能不能整除n,并输出所有能整除n的数. 试将上述算法写成程序. 18.(13分)(2012·济南模拟)某种产品的质量以其质量指标值衡量,质量指标值大于或等于98且小于106的产品为优质品.现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果: A配方的频数分布表 指标值 分组 [90,94) [94,98) [98,102) [102,106) [106,110) 频数 8 20 42 22 8 B配方的频数分布表 指标值 分组 [90,94) [94,98) [98,102) [102,106) [106,110) 频数 4 12 42 32 10 (1)分别估计用A配方,B配方生产的产品的优质品率; (2)由以上统计数据填写2×2列联表,问在犯错误的概率不超过0.1的前提下是否可认为“A配方与B配方的质量有差异”. 19.(13分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据: x 3 4 5 6 y 2.5 3 4 4.5 (1)请画出上表数据的散点图; (2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 (3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? 20.(14分)(易错题)甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下: 甲:82 81 79 78 95 88 93 84 乙:92 95 80 75 83 80 90 85 (1)用茎叶图表示这两组数据,并写出乙组数据的中位数; (2)经过计算知甲、乙两人预赛的平均成绩分别为=85,=85,甲的方差为D1=35.5,乙的方差为D2=41.现要从中选派一人参加数学竞赛,你认为选派哪位学生参加较合适?请说明理由. 21.(14分)某商场庆“五一”实行优惠促销,规定若购物金额x在800元以上(含800元)打8折;若购物金额在500元以上(含500元)打9折;否则不打折.请设计一个算法程序框图,要求输入购物金额x,能输出实际交款额,并写出程序. 答案解析 1.【解析】选C.由题设去掉最高分90,最低分73,所剩数据的平均数为 2.【解析】选B.设甲被抽到的概率为x,单位员工总数为a,由题意知乙被抽到的概率为x. ∴∴x=∴∴a=100, 故选B. 3.【解析】选A.应该评价抗拉强度的大小和波动情况,故应从期望和方差入手. 4.【解析】选A.观察所给的三组数据,①个体没有差异且总数不多可用随机抽样法,是简单随机抽样,②将总体分成均衡的若干部分指的是将总体分段,在第1段内采用简单随机抽样确定一个起始编号,在此编号的基础上加上分段间隔的整数倍即为抽样编号,是系统抽样,③个体有明显的差异,所以选用分层抽样法,是分层抽样,故选A. 【方法技巧】简单随机抽样 简单随机抽样是一种最简单、最基本的抽样方法,常用的简单随机抽样方法有抽签法和随机数法,简单随机抽样中,每个个体被抽取的可能性是相等的. 5.【解题指南】该程序是当型循环,进入依次执行循环,直至结束. 【解析】选A.i从1开始,依次取3,5,7,9,…,当i<8时,循环继续进行,故当i=9时,跳出循环,故输出S=2×7+3=17. 6.【解题指南】求解本题需看懂茎叶图,找出甲、乙的中位数,相加即得. 【解析】选C.由题意知:甲的比赛得分由高到低为: 41,39,37,34,28,26,23,15,13 乙的比赛得分由高到低为: 47,45,38,37,36,33,32,25,24 ∴甲、乙的中位数分别为28,36,故和为64,选C. 7.【解析】选A.在图形中并没有明确的数据分布在区间[55,65)中,但是有[50,60),[60,70)段上的频率分布,据此估计样本在[55,65)上的频率应该在[50,60)和[60,70)的频率分布之间,因为在[50,60)之间的频率为0.02,在[60,70)之间的频率为0.03,由选项可知,选A. 8.【解析】选B.∵甲、乙分数在70、80、90各分数段的打分评委人数一样多,先去掉一个最高分和一个最低分,两名选手的分数都只剩十位数为8的,故只需看个位数的和,乙的个位数字总和为25,甲的个位数字总和为20, ∴a2>a1,故选B. 9.【解析】选B.由所给的程序框图可知其算法为求的值,共有10项,故选B. 10.【解析】选C.∵K2=6.023>5.024, ∴市民收入增减与旅游愿望有关系的可信程度是1-0.025=97.5%.故选C. 11.【解析】由奇数、偶数性质知正整数x除以2的余数为1时为奇数,不为1时为偶数,再由判断框意义知①处应为r=1? 答案:r=1? 12.【解析】依次执行程序得n=3,f(x)=x3;n=3-2=1,f(x)=x;n=1-2=-1,f(x)=x-1, 此时f(x)在(0,+∞)上单调递减,满足退出条件,故输出n的值为-1. 答案:-1 13.【解析】由已知,C专业有1 200-380-420=400名学生,根据分层抽样的方法,可得C专业应抽取名学生. 答案:40 14.【解析】由频率分布直方图可知不及格人数为60×(0.01+0.015)×10=15. 答案:15 15.【解析】由于回归直线方程必过(), 而 ∴4.5=0.95×2+a,解得a=2.6. 答案:2.6 16.【解析】(1)由抽样方法知: 抽取的男生人数为 抽取的女生人数为 (2)男生甲和女生乙被抽到的概率均为0.1. 所以男生甲和女生乙至少有1人被抽到的概率为1-(1-0.1)2=0.19. (3)由(1)知: m=25-(3+8+6)=8,n=20-(2+5+5)=8, 据此估计男生平均分为 女生平均分为 这450名学生的平均分为 17.【解析】 18.【解析】(1)由试验结果知,用A配方生产的产品中优质品的频率为所以用A配方生产的产品的优质品率的估计值为0.64. 由试验结果知,用B配方生产的产品中优质品的频率为所以用B配方生产的产品的优质品率的估计值为0.74. (2)2×2列联表: A配方 B配方 总计 优质品 64 74 138 非优质品 36 26 62 总计 100 100 200 根据题中的数据计算: K2的观测值= 由于2.337 5<2.706,所以在犯错误的概率不超过0.1的前提下不能认为“A配方与B配方的质量有差异”. 19.【解析】(1)如图所示: (2) 故线性回归方程为=0.7x+0.35. (3)根据回归方程的预测,现在生产100吨产品消耗的标准煤的数量为0.7× 100+0.35=70.35, 故能耗减少了90-70.35=19.65(吨标准煤). 20.【解析】(1)作出如图所示的茎叶图,易得乙组数据的中位数为84. (2)派甲参赛比较合适,理由如下: ∵=85,=85,D1=35.5,D2=41, ∴=,D1查看更多
相关文章
- 当前文档收益归属上传用户