- 2021-06-23 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学卷·2018届江苏省连云港市东海高中高二上学期月考数学试卷(行知部) (解析版)
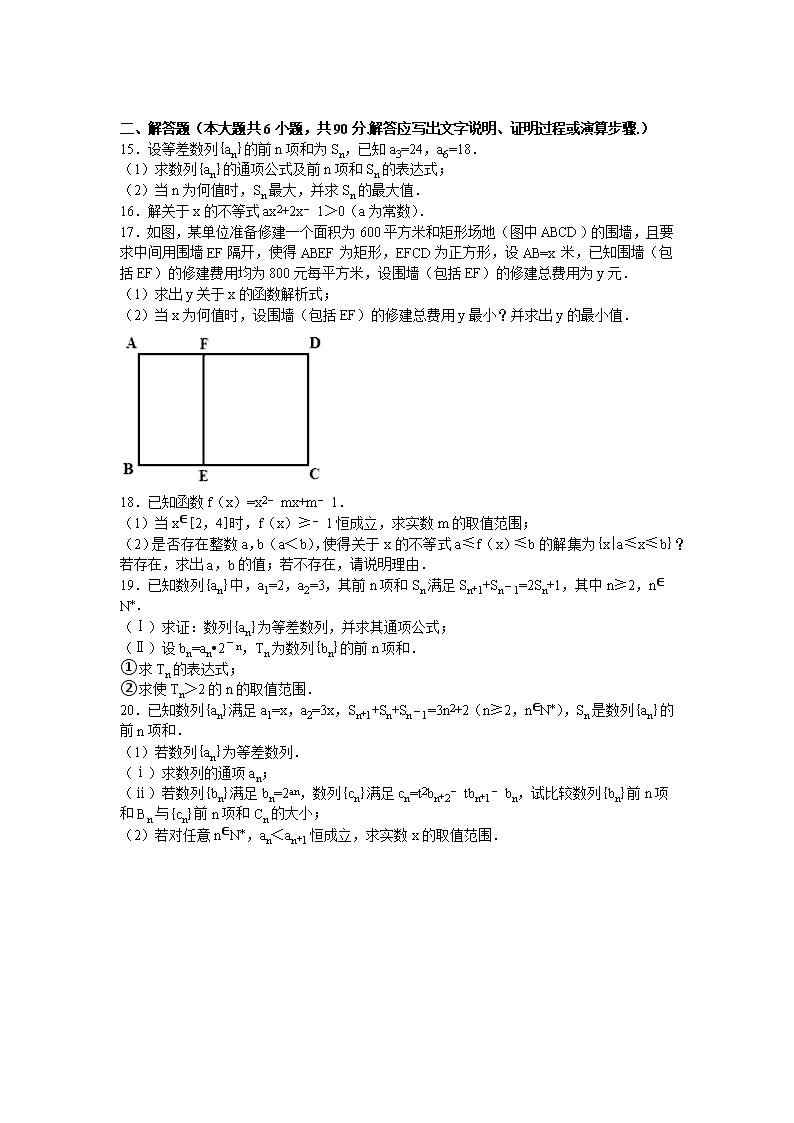
2016-2017学年江苏省连云港市东海高中高二(上)月考数学试卷(行知部) 一、填空题:本大题共14个小题,每小题5分,共70分. 1.不等式<1的解集为 . 2.已知在数列{an}中,a1=﹣1,an+1=2an﹣3,则a5等于 . 3.在1和81之间插入3个实数,使它们与这两个数组成等差数列,则这个等差数列的公差是 . 4.二次函数y=f(x)=ax2+bx+c(x∈R)的部分对应如表: x ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 3 y 6 0 ﹣4 ﹣6 ﹣6 ﹣4 0 6 则关于x的不等式f(x)≤0的解集为 . 5.若一个直角三角形的三边长恰好组成一个公差为2的等差数列,则该三角形的面积是 . 6.若等差数列{an}的第1,3,11项恰好为等比数列{bn}的第3,4,5项,则数列{bn}的公比是 . 7.设实数x,y满足,则z=的取值范围是 . 8.在等差数列{an}中,首项a1=0,公差d≠0,若ak=a1+a2+…+a17,则k= . 9.已知两个等差数列{an},{bn},它们的前n项和分别是Sn,Tn,若=,则= . 10.关于x的不等式ax2+ax+3<0的解集是∅,则a的取值范围是 . 11.已知关于x的不等式2x+≥7在x∈(a,+∞)上恒成立,则实数a的最小值为 . 12.若角α是锐角,则sinα+cosα+的最小值是 . 13.数列{an}满足+++…+=3n+1,则数列{an}的通项公式为an= . 14.设f(i,k)=i•2(k﹣1)(i∈N*,k∈N*),如f(2,3)=2×2(3﹣1)=8.对于正整数m,n,当m≥2,n≥2时,设g(i,n)=f(20,n)+f(21,n)+…+f(2i,n ),S(m,n)=(﹣1)ig(i,n),则S(4,6)= . 二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.) 15.设等差数列{an}的前n项和为Sn,已知a3=24,a6=18. (1)求数列{an}的通项公式及前n项和Sn的表达式; (2)当n为何值时,Sn最大,并求Sn的最大值. 16.解关于x的不等式ax2+2x﹣1>0(a为常数). 17.如图,某单位准备修建一个面积为600平方米和矩形场地(图中ABCD)的围墙,且要求中间用围墙EF隔开,使得ABEF为矩形,EFCD为正方形,设AB=x米,已知围墙(包括EF)的修建费用均为800元每平方米,设围墙(包括EF)的修建总费用为y元. (1)求出y关于x的函数解析式; (2)当x为何值时,设围墙(包括EF)的修建总费用y最小?并求出y的最小值. 18.已知函数f(x)=x2﹣mx+m﹣1. (1)当x∈[2,4]时,f(x)≥﹣1恒成立,求实数m的取值范围; (2)是否存在整数a,b(a<b),使得关于x的不等式a≤f(x)≤b的解集为{x|a≤x≤b}?若存在,求出a,b的值;若不存在,请说明理由. 19.已知数列{an}中,a1=2,a2=3,其前n项和Sn满足Sn+1+Sn﹣1=2Sn+1,其中n≥2,n∈N*. (Ⅰ)求证:数列{an}为等差数列,并求其通项公式; (Ⅱ)设bn=an•2﹣n,Tn为数列{bn}的前n项和. ①求Tn的表达式; ②求使Tn>2的n的取值范围. 20.已知数列{an}满足a1=x,a2=3x,Sn+1+Sn+Sn﹣1=3n2+2(n≥2,n∈N*),Sn是数列{an}的前n项和. (1)若数列{an}为等差数列. (ⅰ)求数列的通项an; (ⅱ)若数列{bn}满足bn=2an,数列{cn}满足cn=t2bn+2﹣tbn+1﹣bn,试比较数列{bn}前n项和Bn与{cn}前n项和Cn的大小; (2)若对任意n∈N*,an<an+1恒成立,求实数x的取值范围. 2016-2017学年江苏省连云港市东海高中高二(上)月考数学试卷(行知部) 参考答案与试题解析 一、填空题:本大题共14个小题,每小题5分,共70分. 1.不等式<1的解集为 (1,+∞)∪(﹣∞,0) . 【考点】其他不等式的解法. 【分析】首先移项通分,等价变形为整式不等式解之 【解答】解:原不等式等价于,即x(x﹣1)>0, 所以不等式的解集为(1,+∞)∪(﹣∞,0); 故答案为:(1,+∞)∪(﹣∞,0) 2.已知在数列{an}中,a1=﹣1,an+1=2an﹣3,则a5等于 ﹣61 . 【考点】数列递推式. 【分析】利用数列的递推关系式逐步求解即可. 【解答】解:在数列{an}中,a1=﹣1,an+1=2an﹣3, 则a2=2a1﹣3=﹣5, a3=2a2﹣3=﹣13, a4=2a3﹣3=﹣29, a5=2a4﹣3=﹣61. 故答案为:﹣61. 3.在1和81之间插入3个实数,使它们与这两个数组成等差数列,则这个等差数列的公差是 20 . 【考点】等差数列. 【分析】利用等差数列的通项公式即可得出. 【解答】解:设这个等差数列的公差为d,由题意可得:81=1+4d,解得d=20. 故答案为:20. 4.二次函数y=f(x)=ax2+bx+c(x∈R)的部分对应如表: x ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 3 y 6 0 ﹣4 ﹣6 ﹣6 ﹣4 0 6 则关于x的不等式f(x)≤0的解集为 [﹣3,2] . 【考点】二次函数的性质. 【分析】由表中数据可看出f(x)过点(﹣3,0),(0,﹣6),(2,0),将这三点的坐标分别带入f(x)便可得出关于a,b,c的方程组,可解出a,b,c的值,从而可以解一元二次不等式f(x)≤0,这样即可得出该不等式的解集. 【解答】解:根据条件知,f(x)过点(﹣3,0),(0,﹣6),(2,0); ∴; 解得; ∴f(x)=x2+x﹣6; ∴解x2+x﹣6≤0得,﹣3≤x≤2; ∴f(x)≤0的解集为[﹣3,2]. 故答案为:[﹣3,2]. 5.若一个直角三角形的三边长恰好组成一个公差为2的等差数列,则该三角形的面积是 24 . 【考点】等差数列的通项公式. 【分析】设此直角三角形的三边分别为:a﹣2,a,a+2,a+2为斜边(a>2),利用勾股定理即可得出. 【解答】解:设此直角三角形的三边分别为:a﹣2,a,a+2,a+2为斜边(a>2), ∴(a﹣2)2+a2=(a+2)2,化为:a2﹣8a=0,a>2,解得a=8. ∴直角边为:6,8. ∴该三角形的面积S==24. 故答案为:24. 6.若等差数列{an}的第1,3,11项恰好为等比数列{bn}的第3,4,5项,则数列{bn}的公比是 1或4 . 【考点】等差数列与等比数列的综合. 【分析】由等比数列等比中项可得: =a1•a11,即(a1+2d)2=a1•(a1+10d),求得4d2=6a1•d,当d=0,q=1,当d≠0,d=a1,由q==4,即可求得q的值. 【解答】解:由题意可得: =a1•a11,即(a1+2d)2=a1•(a1+10d), ∴4d2=6a1•d, 若d=0,q=1, 若d≠0,d=a1, ∴q==4, 故答案为:1或4. 7.设实数x,y满足,则z=的取值范围是 [,] . 【考点】简单线性规划. 【分析】作出不等式组对应的平面区域,利用目标函数的几何意义进行求解即可. 【解答】解:作出不等式组对应的平面区域, z的几何意义是区域内的点到定点D(0,﹣1)的斜率, 由图象知DA的斜率最大,DB的斜率最小, 由得,即A(1,), 由,得,即B(,), DA的斜率k==,DB的斜率k==, 则z的取值范围是[,], 故答案为:[,] 8.在等差数列{an}中,首项a1=0,公差d≠0,若ak=a1+a2+…+a17,则k= 137 . 【考点】数列的求和. 【分析】由ak=a1+a2+…+a17==17a9,再利用通项公式即可得出. 【解答】解:∵ak=a1+a2+…+a17==17a9, ∴0+(k﹣1)d=17(0+8d), ∴k=136+1=137. 故答案为:137. 9.已知两个等差数列{an},{bn},它们的前n项和分别是Sn,Tn,若=,则= . 【考点】等差数列的性质. 【分析】利用等差数列的通项公式、求和公式及其性质即可得出. 【解答】解:由等差数列的性质可得: ===. 故答案为. 10.关于x的不等式ax2+ax+3<0的解集是∅,则a的取值范围是 [0,12] . 【考点】其他不等式的解法. 【分析】由于a作为系数出现,所以讨论a与0的关系,结合二次函数求解集为空集时的a 的范围. 【解答】解:①a=0时,3<0不成立,解集为空集; ②a≠0时,关于x的不等式ax2+ax+3<0的解集是∅,得到,即,解得0<a≤12; 综上a的取值范围是[0,12]. 故答案为:[0,12]. 11.已知关于x的不等式2x+≥7在x∈(a,+∞)上恒成立,则实数a的最小值为 . 【考点】不等式. 【分析】将不等式配凑成基本不等的形式,利用基本不等式求最小值,注意等号成立的条件即可. 【解答】解:∵x>a,∴x﹣a>0, ∴2x+=2(x﹣a)++2a≥2+2a=2a+4, 即2a+4≥7,所以a≥,即a的最小值为 当且仅当x=a+1时取等号. 故答案为. 12.若角α是锐角,则sinα+cosα+的最小值是 3 . 【考点】函数的最值及其几何意义;三角函数的最值. 【分析】由角α是锐角,可得:α+∈(,),进而∈(,1],结合对勾函数的图象和性质,可得sinα+cosα+的最小值. 【解答】解:∵角α是锐角, ∴α+∈(,), ∴∈(,1], 令t=,t∈(,1], 则sinα+cosα+=(t+), ∵y=t+在(0,]上为减函数, 故当t=1,即=1时,sinα+cosα+的最小值是3, 故答案为:3 13.数列{an}满足+++…+=3n+1,则数列{an}的通项公式为an= (2n﹣1)•2•3n . 【考点】数列的求和. 【分析】利用方程组法,两式相减可求数列{an}的通项公式. 【解答】解:数列{an}满足+++…+=3n+1…① 则有: +++…+=3n…②, 由①﹣②可得: =3n+1﹣3n=2•3n ∴an=(2n﹣1)•2•3n 故答案为:(2n﹣1)•2•3n 14.设f(i,k)=i•2(k﹣1)(i∈N*,k∈N*),如f(2,3)=2×2(3﹣1)=8.对于正整数m,n,当m≥2,n≥2时,设g(i,n)=f(20,n)+f(21,n)+…+f(2i,n ),S(m,n)=(﹣1)ig(i,n),则S(4,6)= 640 . 【考点】进行简单的演绎推理. 【分析】直接由新定义求出g(i,n),代入和式后取m=4,n=6进行计算. 【解答】解:由f(i,k)=i•2(k﹣1), 得g(i,n)=f(20,n)+f(21,n)+…+f(2i,n ) =20×2n﹣1+21×2n﹣1+22×2n﹣1+…+2i×2n﹣1 =(1+2+22+…+2i)•2n﹣1 = =(2i+1﹣1)•2n﹣1. 又S(m,n)=(﹣1)ig(i,n), ∴S(4,6)=(﹣1)1•(22﹣1)•25+(﹣1)2•(23﹣1)•25+(﹣1)3•(24﹣1)•25+(﹣1)4•(25﹣1)•25 =(﹣3+7﹣15+31)×32=640. 故答案为:640. 二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.) 15.设等差数列{an}的前n项和为Sn,已知a3=24,a6=18. (1)求数列{an}的通项公式及前n项和Sn的表达式; (2)当n为何值时,Sn最大,并求Sn的最大值. 【考点】等差数列的性质. 【分析】(1)由题意易得数列的公差,进而可通项公式及前n项和Sn的表达式; (2)利用二次函数的性质求前n项和的最大值. 【解答】解:(1)设等差数列{an}的公差为d,则, 解得, 所以an=a1+(n﹣1)d=28﹣2(n﹣1)=30﹣2n, Sn===﹣n2+29n,即Sn=﹣n2+29n. (2)Sn=﹣n2+29n=﹣(n﹣)2+()2, 又因为n∈N*,所以,当n=14或15时,Sn最大,最大值为210. 16.解关于x的不等式ax2+2x﹣1>0(a为常数). 【考点】一元二次不等式的解法. 【分析】讨论a的取值,求对应不等式的解集即可. 【解答】解:当a=0时,2x﹣1>0,解得x>, 所以原不等式的解集为(,+∞); 当a≠0时,一元二次方程ax2+2x﹣1=0的判别式△=4+4a, 当a≤﹣1时,△≤0,原不等式的解集为∅; 当a>0时,方程ax2+2x﹣1=0的两个实数根为x1=,x2=; 原不等式的解集为{x|x>或x<}; 当﹣1<a<0时,x1<x2, 原不等式的解集为{x|<x<}. 17.如图,某单位准备修建一个面积为600平方米和矩形场地(图中ABCD)的围墙,且要求中间用围墙EF隔开,使得ABEF为矩形,EFCD为正方形,设AB=x米,已知围墙(包括EF)的修建费用均为800元每平方米,设围墙(包括EF)的修建总费用为y元. (1)求出y关于x的函数解析式; (2)当x为何值时,设围墙(包括EF)的修建总费用y最小?并求出y的最小值. 【考点】函数模型的选择与应用. 【分析】(1)根据面积确定AD的长,利用围墙(包括EF)的修建费用均为800元每平方米,即可求得函数的解析式; (2)根据函数的特点,满足一正二定的条件,利用基本不等式,即可确定函数的最值. 【解答】解:(1)设AD=t米,则由题意得xt=600,且t>x,故,可得,… (说明:若缺少“”扣2分) 则, 所以y关于x的函数解析式为. (2), 当且仅当,即x=20时等号成立. 故当x为20米时,y最小.y的最小值为96000元.… 18.已知函数f(x)=x2﹣mx+m﹣1. (1)当x∈[2,4]时,f(x)≥﹣1恒成立,求实数m的取值范围; (2)是否存在整数a,b(a<b),使得关于x的不等式a≤f(x)≤b的解集为{x|a≤x≤b}?若存在,求出a,b的值;若不存在,请说明理由. 【考点】一元二次不等式的解法;二次函数在闭区间上的最值. 【分析】(1)函数f(x)=x2﹣mx+m﹣1=+m﹣1.对与2,4的关系分类讨论,利用二次函数的单调性即可得出; (2)假设存在整数a,b(a<b),使得关于x的不等式a≤f(x)≤b的解集为{x|a≤x≤b}.即a≤x2﹣mx+m﹣1≤b的解集为{x|a≤x≤b}.可得f(a)=a,f(b)=b.即x2﹣mx+m﹣1=x的两个实数根为a,b.即可得出. 【解答】解:(1)函数f(x)=x2﹣mx+m﹣1=+m﹣1. ①当,即m≤4时,函数f(x)在x∈[2,4]单调递增, ∵f(x)≥﹣1恒成立,∴f(2)=﹣m+3≥﹣1,解得m≤4. ∴m≤4满足条件. ②当≥4,即m≥8时,函数f(x)在x∈[2,4]单调递减, ∵f(x)≥﹣1恒成立,∴f(4)=﹣3m+15≥﹣1,解得m≤. ∴不满足m≥8,应该舍去. ③当,即4<m<8时,当x=时,函数f(x)取得最小值, ∵f(x)≥﹣1恒成立,∴f()=﹣+m﹣1≥﹣1,解得0≤m≤4,不满足4<m<8,应舍去. 综上可得:实数m的取值范围是(﹣∞,4]. (2)假设存在整数a,b(a<b),使得关于x的不等式a≤f(x)≤b的解集为{x|a≤x≤b}. 即a≤x2﹣mx+m﹣1≤b的解集为{x|a≤x≤b}.则f(a)=a,f(b)=b. ∴x2﹣mx+m﹣1=x的两个实数根为a,b. ∴a+b=m+1,ab=m﹣1. 当b=1时,a不存在,舍去; 当b≠1时,a=1﹣,只有b=2或0时,可得a=0,2. 又a<b, ∴存在整数时,使得关于x的不等式a≤f(x)≤b的解集为{x|a≤x≤b}. 19.已知数列{an}中,a1=2,a2=3,其前n项和Sn满足Sn+1+Sn﹣1=2Sn+1,其中n≥2,n∈N*. (Ⅰ)求证:数列{an}为等差数列,并求其通项公式; (Ⅱ)设bn=an•2﹣n,Tn为数列{bn}的前n项和. ①求Tn的表达式; ②求使Tn>2的n的取值范围. 【考点】数列的求和;等差数列的通项公式. 【分析】(Ⅰ)把Sn+1+Sn﹣1=2Sn+1整理为:(sn+1﹣sn)﹣(sn﹣sn﹣1)=1,即an+1﹣an=1 即可说明数列{an}为等差数列;再结合其首项和公差即可求出{an}的通项公式; (Ⅱ)因为数列{bn}的通项公式为一等差数列乘一等比数列组合而成的新数列,故直接利用错位相减法求和即可 【解答】解:(1)∵数列{an}中,a1=2,a2=3,其前n项和Sn满足Sn+1+Sn﹣1=2Sn+1,其中n≥2,n∈N*, ∴(Sn+1﹣Sn)﹣(Sn﹣Sn﹣1)=1(n≥2,n∈N*,), ∴a2﹣a1=1, ∴数列{an}是以a1=2为首项,公差为1的等差数列, ∴an=n+1; (2)∵an=n+1; ∴bn=an•2﹣n=(n+1)2﹣n, ∴Tn=2×+3×+…+n+(n+1)…(1) =2×+3×+…+n+(n+1)…(2) (1)﹣(2)得: Tn=1++…+﹣(n+1), ∴Tn=3﹣, 代入不等式得:3﹣>2,即, 设f(n)=﹣1,f(n+1)﹣f(n)=﹣<0, ∴f(n)在N+上单调递减, ∵f(1)=1>0,f(2)=>0,f(3)=﹣<0, ∴当n=1,n=2时,f(n)>0;当n≥3,f(n)<0, 所以n的取值范围为n≥3,且n∈N*. 20.已知数列{an}满足a1=x,a2=3x,Sn+1+Sn+Sn﹣1=3n2+2(n≥2,n∈N*),Sn是数列{an}的前n项和. (1)若数列{an}为等差数列. (ⅰ)求数列的通项an; (ⅱ)若数列{bn}满足bn=2an,数列{cn}满足cn=t2bn+2﹣tbn+1﹣bn,试比较数列{bn}前n项和Bn与{cn}前n项和Cn的大小; (2)若对任意n∈N*,an<an+1恒成立,求实数x的取值范围. 【考点】数列的求和;数列递推式. 【分析】(1)(ⅰ)由条件可得S3+S2+S1=14,即a3+2a2+3a1=14,求得a3=14﹣9x,再由等差数列的性质,可得x=1,进而得到通项公式; (ⅱ)其前n项和Bn>0,将前n项和Bn与{cn}前n项和Cn作差,讨论t的范围,即可得到大小关系; (2)将n换为n+1,两式作差,再将n换为n+1,两式作差,可得,再由数列的单调性,可得不等式,解得即可得到所求范围. 【解答】解:(1)(ⅰ)因为, 所以S3+S2+S1=14, 即a3+2a2+3a1=14,又a1=x,a2=3x, 所以a3=14﹣9x, 又因为数列{an}成等差数列,所以2a2=a1+a3, 即6x=x+(14﹣9x),解得x=1, 所以; (ⅱ)因为,所以,其前n项和Bn>0, 又因为, 所以其前n项和,所以, 当或时,Cn>Bn; 当或时,Cn=Bn; 当时,Cn<Bn. (2)由, 知, 两式作差,得, 所以, 作差得, 所以,当n=1时,an=a1=x; 当n=3k﹣1时,an=a3k﹣1=a2+(k﹣1)×6=3x+6k﹣6=2n+3x﹣4; 当n=3k时,an=a3k=a3+(k﹣1)×6=14﹣9x+6k﹣6=2n﹣9x+8; 当n=3k+1时,an=a3k+1=a4+(k﹣1)×6=1+6x+6k﹣6=2n+6x﹣7; 因为对任意n∈N*,an<an+1恒成立, 所以a1<a2且a3k﹣1<a3k<a3k+1<a3k+2, 所以,解得,, 故实数x的取值范围为. 查看更多