2018届二轮复习不等式选讲学案
第2讲 不等式选讲
高考定位 本部分主要考查绝对值不等式的解法.求含绝对值的函数的最值及求含参数的绝对值不等式中的参数的取值范围,不等式的证明等,结合集合的运算、函数的图象和性质、恒成立问题及基本不等式,绝对值不等式的应用成为命题的热点,主要考查基本运算能力与推理论证能力及数形结合思想、分类讨论思想.
真 题 感 悟
1.(2017·全国Ⅰ卷)已知函数f(x)=-x2+ax+4,g(x)=|x+1|+|x-1|.
(1)当a=1时,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[-1,1],求a的取值范围.
解 (1)当a=1时,f(x)=-x2+x+4,g(x)=|x+1|+|x-1|=
①当x>1时,f(x)≥g(x)⇔-x2+x+4≥2x,
解之得1
0,b>0,且a3+b3=2.
证明:(1)(a+b)(a5+b5)≥4;
(2)a+b≤2.
证明 (1)(a+b)(a5+b5)=a6+ab5+a5b+b6
=(a3+b3)2-2a3b3+ab(a4+b4)=4+ab(a2-b2)2≥4.
(2)因为(a+b)3=a3+3a2b+3ab2+b3=2+3ab(a+b)来源:Z*xx*k.Com]
≤2+(a+b)=2+,
所以(a+b)3≤8,因此a+b≤2.
考 点 整 合
1.绝对值不等式的性质
定理1:如果a,b是实数,则|a+b|≤|a|+|b|,当且仅当ab≥0时,等号成立.
定理2:如果a,b,c是实数,那么|a-c|≤|a-b|+|b-c|,当且仅当(a-b)(b-c)≥0时,等号成立.
2.|ax+b|≤c,|ax+b|≥c(c>0)型不等式的解法
(1)|ax+b|≤c⇔-c≤ax+b≤c.
(2)|ax+b|≥c⇔ax+b≥c或ax+b≤-c.
3.|x-a|+|x-b|≥c,|x-a|+|x-b|≤c(c>0)型不等式的解法
(1)利用绝对值不等式的几何意义直观求解.
(2)利用零点分段法求解.
(3)构造函数,利用函数的图象求解.
4.基本不等式
定理1:设a,b∈R,则a2+b2≥2ab.当且仅当a=b时,等号成立.
定理2:如果a,b为正数,则≥,当且仅当a=b时,等号成立.
定理3:如果a,b,c为正数,则≥,当且仅当a=b=c时,等号成立.
定理4:(一般形式的算术—几何平均不等式)如果a1,a2,…,an为n个正数,则≥,当且仅当a1=a2=…=an时,等号成立.[来源:学+科+网]
热点一 绝对值不等式的解法
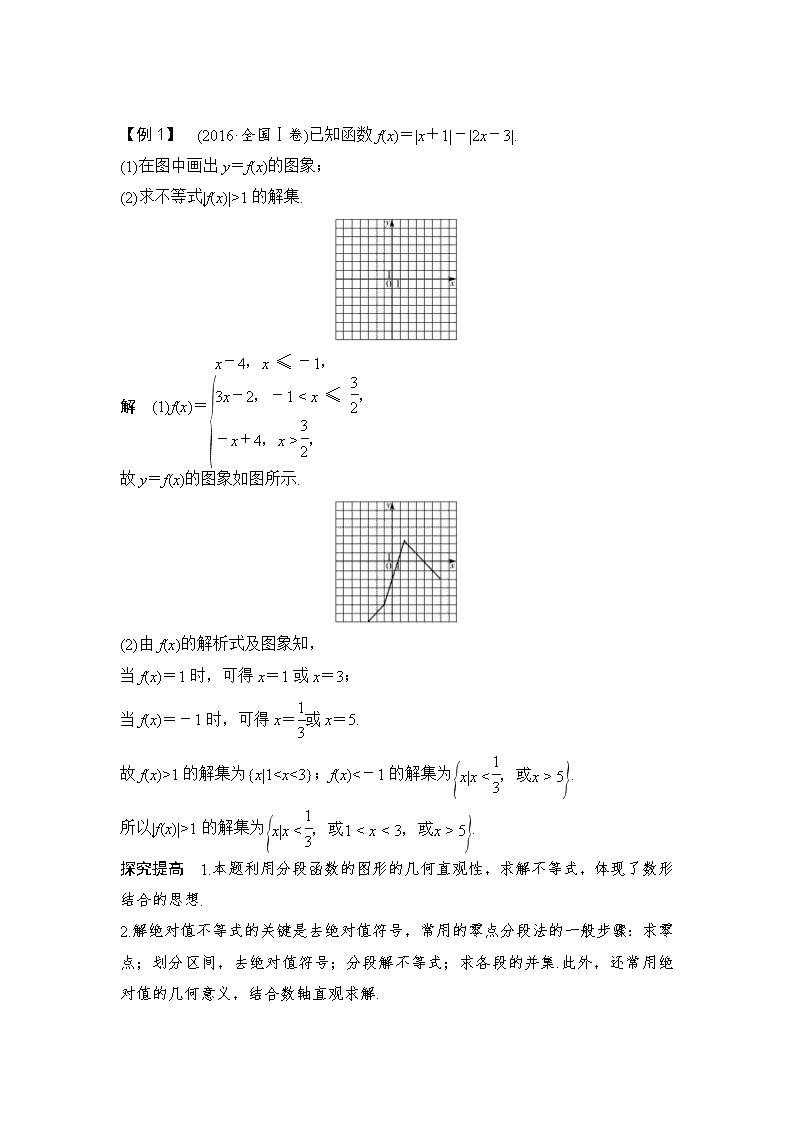
【例1】 (2016·全国Ⅰ卷)已知函数f(x)=|x+1|-|2x-3|.
(1)在图中画出y=f(x)的图象;
(2)求不等式|f(x)|>1的解集.
解 (1)f(x)=
故y=f(x)的图象如图所示.
(2)由f(x)的解析式及图象知,
当f(x)=1时,可得x=1或x=3;
当f(x)=-1时,可得x=或x=5.
故f(x)>1的解集为{x|11的解集为.
探究提高 1.本题利用分段函数的图形的几何直观性,求解不等式,体现了数形结合的思想.
2.解绝对值不等式的关键是去绝对值符号,常用的零点分段法的一般步骤:求零点;划分区间,去绝对值符号;分段解不等式;求各段的并集.此外,还常用绝对值的几何意义,结合数轴直观求解.
【训练1】 (2015·全国Ⅰ卷)已知函数f(x)=|x+1|-2|x-a|,a>0.
(1)当a=1时,求不等式f(x)>1的解集;
(2)若f(x)的图象与x轴围成的三角形面积大于6,求a的取值范围.
解 (1)当a=1时,f(x)>1化为|x+1|-2|x-1|-1>0.
当x≤-1时,不等式化为x-4>0,无解;
当-10,解得0,解得1≤x<2.
所以f(x)>1的解集为.
(2)由题设可得,f(x)=
所以函数f(x)的图象与x轴围成的三角形的三个顶点分别为A,B(2a+1,0),C(a,a+1),
△ABC的面积S=|AB|·(a+1)=(a+1)2.
由题设得(a+1)2>6,故a>2.
所以a的取值范围为(2,+∞).
热点二 不等式的证明
【例2】 (2017·长沙调研)已知f(x)=|2x-1|+x+的最小值为m.
(1)求m的值;
(2)已知a,b,c是正实数,且a+b+c=m,求证:2(a3+b3+c3)≥ab+bc+ca-3abc.
(1)解 当x≥时,f(x)=3x-在上单调递增,且f(x)≥-=1;
当x<时,f (x)=-x在上单调递减,且f(x)>-=1.
综上可得x=时,f(x)取得最小值1,即m=1.
(2)证明 a,b,c是正实数,且a+b+c=1,
由a3+b3-a2b-b2a=a2(a-b)+b2(b-a)
=(a-b)(a2-b2)=(a+b)(a-b)2≥0,
则有a3+b3-a2b-b2a≥0,
即a3+b3≥a2b+b2a=ab(a+b)=ab(1-c)=ab-abc,
所以a3+b3≥ab-abc.
同理可得b3+c3≥bc-abc;c3+a3≥ca-abc.
上面三式相加得,2(a3+b3+c3)≥ab+bc+ca-3abc,当且仅当a=b=c=取得等号.
探究提高 1.证明不等式的基本方法有比较法、综合法、分析法和反证法,其中比较法和综合法是基础,综合法证明的关键是找到证明的切入点.
2.当要证的不等式较难发现条件和结论之间的关系时,可用分析法来寻找证明途径,使用分析法证明的关键是推理的每一步必须可逆.如果待证命题是否定性命题、唯一性命题或以“至少”“至多”等方式给出的,则考虑用反证法.
【训练2】 (2015·全国Ⅱ卷)设a, b,c,d均为正数,且a+b=c+d,证明:
(1)若ab>cd,则+>+;
(2)+>+是|a-b|<|c-d|的充要条件.
证明 (1)∵a,b,c,d为正数,且a+b=c+d,
欲证+>+,只需证明(+)2>(+)2,
也就是证明a+b+2>c+d+2,
只需证明>,即证ab>cd.
由于ab>cd,因此+>+.
(2)①若|a-b|<|c-d|,则(a-b)2<(c-d)2,
即(a+b)2-4ab<(c+d)2-4cd.
∵a+b=c+d,所以ab>cd.
由(1)得+>+.
②若+>+,则(+)2>(+)2,
∴a+b+2>c+d+2.
∵a+b=c+d,所以ab>cd.
于是(a-b)2=(a+b)2-4ab<(c+d)2-4cd=(c-d)2.
因此|a-b|<|c-d|.
综上,+>+是|a-b|<|c-d|的充要条件.
热点三 与绝对值不等式有关的最值问题
【例3】 (2017·全国Ⅲ卷)已知函数f(x)=|x+1|-|x-2|.
(1)求不等式f(x)≥1的解集;
(2)若不等式f(x)≥x2-x+m的解集非空,求m的取值范围.
解 (1)f(x)=|x+1|-|x-2|=
由f(x)≥1可得
①当x≤-1时显然不满足题意;
②当-1m2,
又不等式|x-m|<|x|的解集为(1,+∞),
则1是方程2mx=m2的解,解得m=2(m=0舍去).
(2)∵m=2,∴不等式<-<对x∈(0,+∞)恒成立等价于不等式a-5<|x+1|-|x-2|0,|x-1|<,|y-2|<,求证|2x+y-4|L(A,C),求x的取值范围;
(2)当x∈R时,不等式L(A,B)≤t+L(A,C)恒成立,求t的最小值.
解 (1)由定义得|x-1|+1>|x-5|+1,
则|x-1|>|x-5|,两边平方得8x>24,解得x>3.
故x的取值范围为(3,+∞).
(2)当x∈R时,不等式|x-1|≤|x-5|+t恒成立,也就是t≥|x-1|-|x-5|恒成立,
因为|x-1|-|x-5|≤|(x-1)-(x-5)|=4,
所以t≥4,tmin=4.
故t的最小值为4.
3.(2016·全国Ⅱ卷)已知函数f(x)=+,
M为不等式f(x)<2的解集.
(1)求M;
(2)证明:当a,b∈M时,|a+b|<|1+ab|.
(1)解 f(x)=
当x≤-时,由f(x)<2得-2x<2,
解得x>-1,所以-10;
(2)若∃x0∈R,使得f(x0)+2m2<4m,求实数m的取值范围.
解 (1)①当x<-2时,f(x)=1-2x+x+2=-x+3.
令-x+3>0,解得x<3,从而x<-2.
②当-2≤x≤时,f(x)=1-2x-x-2=-3x-1,
令-3x-1>0,解得x<-,
又∵-2≤x≤,∴-2≤x<-.
③当x>时,f(x)=2x-1-x-2=x-3,
令x-3>0,解得x>3.
又∵x>,∴x>3.
综上,不等式f(x)>0的解集为∪(3,+∞).
(2)由(1)得f(x)=
∴f(x)min=f=-.
∵∃x0∈R,使得f(x0)+2m2<4m,
∴4m-2m2>-,
整理得4m2-8m-5<0,解得-1,f(α)+f(β)=6,求证:+≥.
(1)解 因为|x-m|+|x|≥|x-m-x|=|m|,
要使|x-m|+|x|<2有解,则|m|<2,解得-21,f(α)+f(β)=2α-1+2β-1=6,
∴α+β=4,
∴+≥(α+β)
=≥=,
当且仅当=,即α=,β=时“=”成立,
故+≥.