2021高考数学大一轮复习考点规范练33二元一次不等式组与简单的线性规划问题理新人教A版
考点规范练33 二元一次不等式(组)与简单的线性规划问题
考点规范练A册第22页
基础巩固
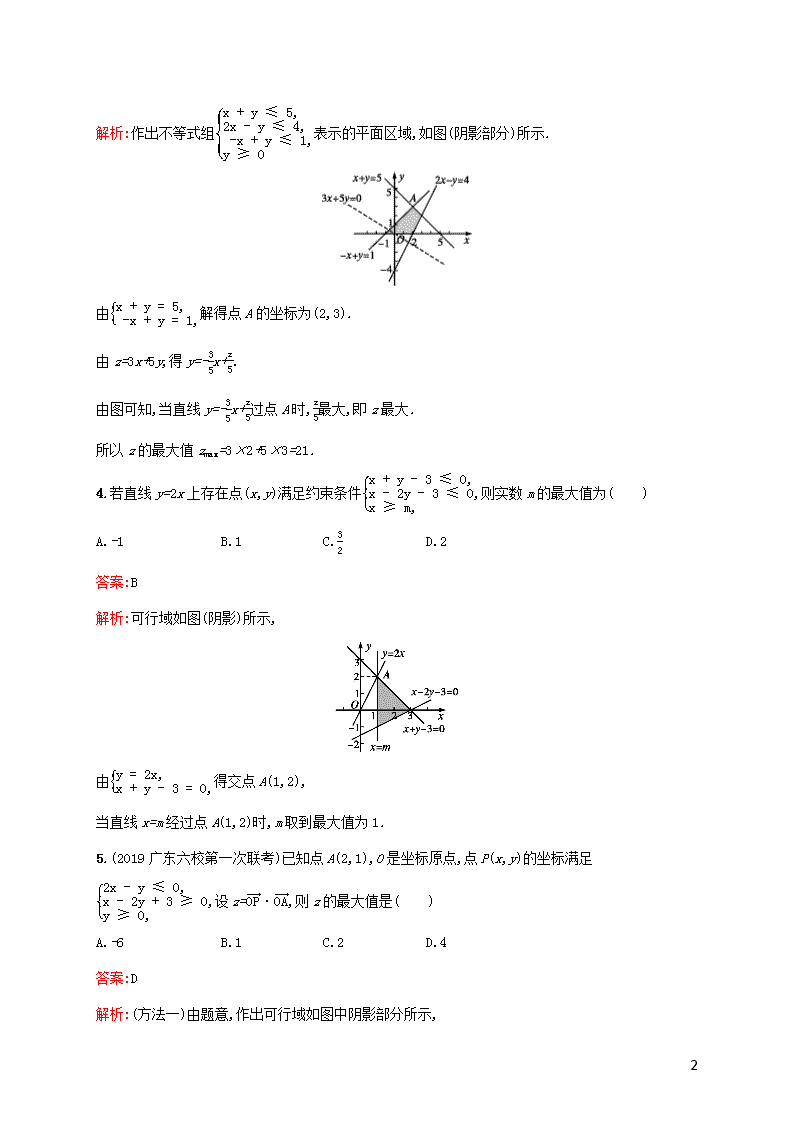
1.若点(1,b)在两条平行直线6x-8y+1=0和3x-4y+5=0 之间,则b应取的整数值为( )
A.2 B.1 C.3 D.0
答案:B
解析:由题意知(6-8b+1)(3-4b+5)<0,即b-78(b-2)<0,解得78
zC或zA=zC>zB或zB=zC>zA,解得a=-1或a=2.
10
(方法二)目标函数z=y-ax可化为y=ax+z,令l0:y=ax,平移l0,则当l0∥AB或l0∥AC时符合题意,故a=-1或a=2.
14.若不等式组x+y-2≤0,x+2y-2≥0,x-y+2m≥0表示的平面区域为三角形,且其面积等于43,则m的值为( )
A.-3 B.1 C.43 D.3
答案:B
解析:如图,要使不等式组表示的平面区域为三角形,则不等式x-y+2m≥0表示的平面区域为直线x-y+2m=0下方的区域,且-2m<2,即m>-1.这时平面区域为△ABC.
由x+y-2=0,x+2y-2=0,解得x=2,y=0,则A(2,0).
由x+y-2=0,x-y+2m=0,解得x=1-m,y=1+m,
则B(1-m,1+m).
同理C2-4m3,2+2m3,M(-2m,0).
S△ABC=S△ABM-S△ACM=12·(2+2m)·(1+m)-2+2m3=(m+1)23,由已知得(m+1)23=43,解得m=1(m=-3<-1舍去).
15.(2019广东蕉岭中学高三一模)已知D=(x,y)x+y-2≤0,x-y+2≤0,3x-y+6≥0,给出下列四个命题:
p1:∀(x,y)∈D,x+y≥0;p2:∀(x,y)∈D,2x-y+1≤0;p3:∃(x,y)∈D,y+1x-1≤-4;p4:∃(x,y)∈D,x2+y2≥2.
其中是真命题的是( )
A.p1,p2 B.p2,p3 C.p3,p4 D.p2,p4
10
答案:D
解析:可行域为一个△ABC及其内部,其中A(-2,0),B(0,2),C(-1,3),所以直线z=x+y过点A时取最小值-2<0;z=2x-y+1过点B时取最大值-1;斜率y+1x-1的最小值为2+10-1=-3>-4;到原点距离的平方的最小值为|0-0+2|22=2,因此选D.
16.电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:
连续剧播放
时长/min
广告播放
时长/min
收视人次
/万
甲
70
5
60
乙
60
5
25
已知电视台每周安排的甲、乙连续剧的总播放时间不多于600 min,广告的总播放时间不少于30 min,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用x,y表示每周计划播出的甲、乙两套连续剧的次数.
(1)用x,y列出满足题目条件的数学关系式,并画出相应的平面区域;
(2)问电视台每周播出甲、乙两套连续剧各多少次,才能使总收视人次最多?
解:(1)由已知,x,y满足的数学关系式为70x+60y≤600,5x+5y≥30,x≤2y,x≥0,y≥0
即7x+6y≤60,x+y≥6,x-2y≤0,x≥0,y≥0,
该二元一次不等式组所表示的平面区域为图①中的阴影部分:
10
图①
(2)设总收视人次为z万,则目标函数为z=60x+25y.
考虑z=60x+25y,将它变形为y=-125z+z25,
这是斜率为-125,随z变化的一族平行直线,z25为直线在y轴上的截距,当z25取得最大值时,z的值最大.
又因为x,y满足约束条件,所以由图②可知,当直线z=60x+25y经过可行域上的点M时,截距z25最大,即z最大.
解方程组7x+6y=60,x-2y=0,得点M的坐标为(6,3).
所以,电视台每周播出甲连续剧6次、乙连续剧3次时才能使总收视人次最多.
图②
高考预测
17.若变量x,y满足约束条件4x+5y≥8,1≤x≤3,0≤y≤2,则z=3x+2y的最小值为( )
A.4 B.235 C.6 D.315
答案:B
解析:作出题中约束条件表示的可行域,如图(阴影部分)所示,
10
由z=3x+2y可得y=-32x+z2.
z2指的是直线y=-32x+z2在y轴上的截距,根据图形可知,当直线y=-32x+z2通过点A时,可使z2取得最小值,即z取得最小值.
易知点A的坐标为1,45,所以zmin=3×1+2×45=235.
10