高一必修1典例选讲及配套习题 第8讲 映射与函数的概念

高一必修1典例选讲及配套习题 第8讲 映射与函数的概念

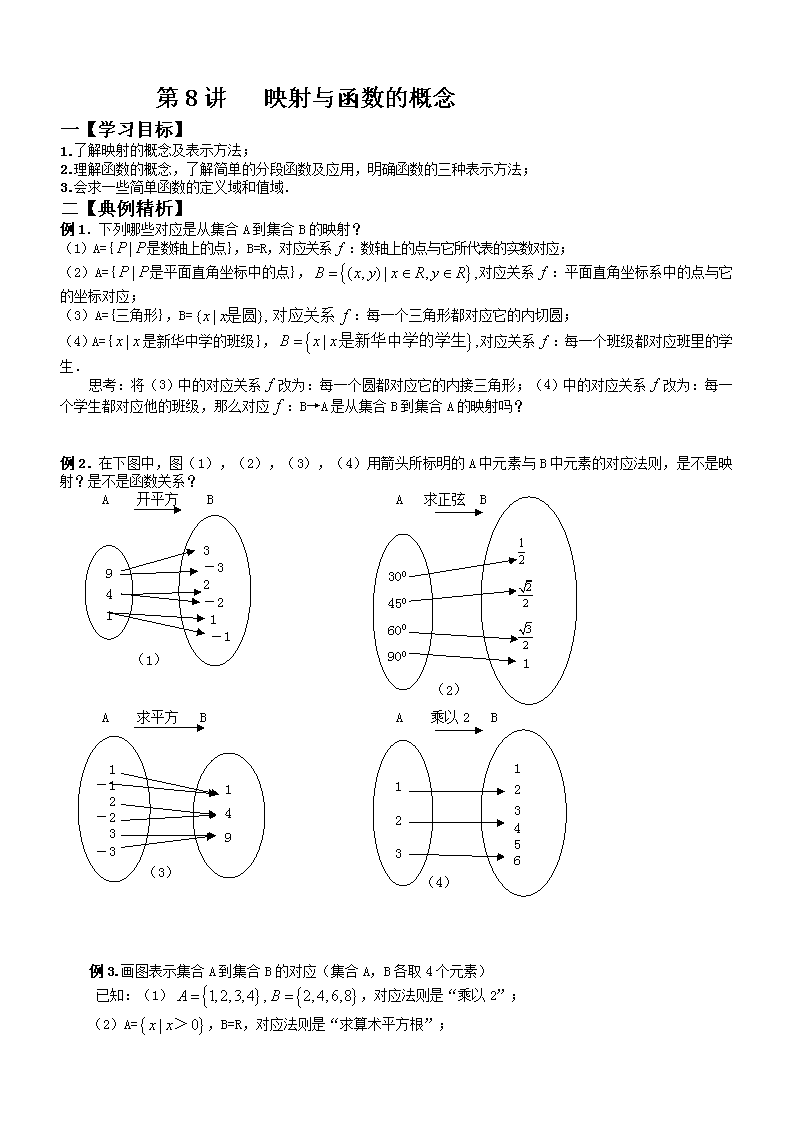
第8讲 映射与函数的概念 一【学习目标】‎ ‎1.了解映射的概念及表示方法；‎ ‎2.理解函数的概念，了解简单的分段函数及应用，明确函数的三种表示方法；‎ ‎3.会求一些简单函数的定义域和值域.‎ 二【典例精析】‎ 例1．下列哪些对应是从集合A到集合B的映射？‎ ‎（1）A={是数轴上的点}，B=R，对应关系：数轴上的点与它所代表的实数对应；‎ ‎（2）A={是平面直角坐标中的点}，对应关系：平面直角坐标系中的点与它的坐标对应；‎ ‎（3）A={三角形}，B=：每一个三角形都对应它的内切圆；‎ ‎（4）A={是新华中学的班级}，对应关系：每一个班级都对应班里的学生．‎ 思考：将（3）中的对应关系改为：每一个圆都对应它的内接三角形；（4）中的对应关系改为：每一个学生都对应他的班级，那么对应：B→A是从集合B到集合A的映射吗？‎ 例2．在下图中，图（1），（2），（3），（4）用箭头所标明的A中元素与B中元素的对应法则，是不是映射？是不是函数关系？‎ ‎300‎ ‎450‎ ‎600‎ ‎900‎ ‎1‎ ‎（2）‎ A 开平方 B A 求正弦 B ‎9‎ ‎4‎ ‎1‎ ‎3‎ ‎－3‎ ‎2‎ ‎－2‎ ‎1‎ ‎－1‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎（1）‎ ‎ ‎ ‎1‎ ‎2‎ ‎3‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎（4）‎ A 求平方 B A 乘以2 B ‎1‎ ‎－1‎ ‎2‎ ‎－2‎ ‎3‎ ‎－3‎ ‎1‎ ‎4‎ ‎9‎ ‎（3）‎ ‎ ‎ 例3.画图表示集合A到集合B的对应（集合A，B各取4个元素）‎ 已知：（1），对应法则是“乘以2”；‎ ‎（2）A=＞，B=R，对应法则是“求算术平方根”；‎ ‎（3），对应法则是“求倒数”；‎ ‎（4）＜对应法则是“求余弦”．‎ 例4．在下图中的映射中，A中元素600的象是什么？B中元素的原象是什么？‎ ‎300‎ ‎450‎ ‎600‎ ‎900‎ ‎1‎ ‎ A 求正弦 B ‎ ‎ 例5.已知函数f(x)=+‎ ‎（1）求函数的定义域；‎ ‎（2）求f（－3），f()的值；‎ ‎（3）当a＞0时，求f（a）,f(a－1)的值.‎ 例6.设一个矩形周长为80，其中一边长为x，求它的面积关于x的函数的解析式，并写出定义域.‎ 例7.下列函数中哪个与函数y=x相等？‎ ‎（1）y=()2 ; （2）y=() ;‎ ‎（3）y= ; （4）y=‎ 例8．某种笔记本的单价是5元，买个笔记本需要元，试用三种表示法表示函数 ‎．‎ 例9．某市郊空调公共汽车的票价按下列规则制定：‎ ‎（1）乘坐汽车5公里以内，票价2元；‎ ‎（2）5公里以上，每增加5公里，票价增加1元（不足5公里按5公里计算），已知两个相邻的公共汽车站间相距约为1公里，如果沿途（包括起点站和终点站）设20个汽车站，请根据题意，写出票价与里程之间的函数解析式，并画出函数的图象．‎ 三【过关精练】‎ 一、选择题 ‎1.已知集合，，，映射是从M到N的一个函数，则的值为（ ）‎ A．2 B．3 C．4 D．5‎ ‎2.给出下列四个图形，其中能表示从集合M到集合N的函数关系的有（ ）‎ A.0个 B.1个 C.2个 D.3个 ‎ ‎x x x x ‎1‎ ‎2‎ ‎1‎ ‎1‎ ‎1‎ ‎2‎ ‎2‎ ‎2‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎2‎ ‎2‎ ‎2‎ ‎2‎ y y y y ‎3‎ O O O O ‎3.设函数则的值为（ ）‎ A． B． C． D．‎  ‎4.若函数的定义域是，则函数的定义域是（ ）‎ A． B． C． D．‎ ‎5．设函数f(x)对任意x、y满足f(x＋y)=f(x)＋f(y)，且f(2)=4，则f(－1)的值为（ ）‎ A．－2 B．± C．±1 D．2‎ ‎6．已知函数f(＋1)=x＋1，则函数f(x)的解析式为（ ）‎ A．f(x)=x2 B．f(x)=x2＋1(x≥1)‎ C．f(x)=x2－2x(x≥1) D．f(x)=x2－2x＋2(x≥1)‎ ‎7．下列各组中，函数f(x)和g(x)的图象相同的是（ ）‎ A．f(x)=x，g(x)=()2 B．f(x)=1，g(x)=x0‎ C．f(x)=|x|，g(x)= D．f(x)=|x|，g(x)=‎ 二、填空题 ‎8.已知函数且，则 方程f(x)=x解的个数为 ‎ ‎9.设函数则不等式的解集是 ‎ ‎10.已知函数,其中是的正比例函数,是的反比 例函数，且,则 . 三、解答题 ‎11.（1）若函数的定义域为，求的定义域；‎ ‎（2）若函数的定义域为，求函数的定义域.‎ ‎12.已知函数. ‎（1）若函数的值域为［0，+∞)时的的值； ‎（2）若函数的值均为非负值，求函数的值域. 答案 例6解：由题意知，另一边长为，且边长为正数，所以0＜x＜40.‎ 所以S==（40－x）x（0＜x＜40）‎